《概率论与数理统计》课程教学资源（试卷习题）2008-2009学年第一学期考试试题（题目）

.内蒙古科技大学2008/2009学年第一学期《概率论与数理统计》考试试题课程号：68132106考试方式：闭卷任课教师：使用专业、年级：工科2007级备注：考试时间：阅卷成绩登记表（阅卷、核分教师填写）四五六七题号三总分二得分阅卷人、选择题（共6题，每题3分，共18分）1. 设0< P(A)<1, 0< P(B)<1, P(A|B)+ P(A|B)=1,则 (（A）事件A与B互不相容（B）事件A与B互相对立（C）事件A与B互不独立（D）事件A与B相互独立e-(-00<x<+o0)，则其分布函数2.设随机变量X的概率密度为f(x)=2)F(x)为（....各索毛点1[.0x<0一e.x<02(A) F(x)(B) F(x)-1x≥0x≥02etx<012x<01(C) F(x)(D) F(x)=0≤x<1*22班毛点x≥0x≥1+.........3.设随机变量X和Y相互独立，且X~N(,),Y～N(uz,,)，则)Z=X+Y服从（

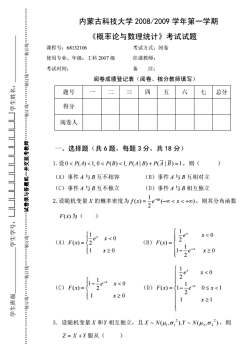
内蒙古科技大学 2008/2009 学年第一学期 《概率论与数理统计》考试试题 课程号：68132106 考试方式：闭卷 使用专业、年级：工科 2007 级 任课教师： 考试时间： 备 注： 阅卷成绩登记表（阅卷、核分教师填写） 题号 一 二 三 四 五 六 七 总分 得分 阅卷人 一、选择题（共 6 题，每题 3 分，共 18 分） 1.设0 < P(A) < 1, 0 < P(B) < 1, P(A | B) + P(A | B) = 1，则（ ） （A）事件 A 与 B 互不相容 （B）事件 A 与 B 互相对立 （C）事件 A 与 B 互不独立 （D）事件 A 与 B 相互独立 2.设随机变量 X 的概率密度为 ( ) 2 1 ( ) | | = -¥ < < +¥ - f x e x x ，则其分布函数 F(x)为（ ） （A） ï î ï í ì ³ < = 1 0 0 2 1 ( ) x e x F x x （B） ï ï î ï ï í ì - ³ < = - 0 2 1 1 0 2 1 ( ) e x e x F x x x （C） ï î ï í ì ³ - < = - 1 0 0 2 1 1 ( ) x e x F x x （D） ï ï ï î ï ï ï í ì ³ - £ < < = - 1 1 0 1 2 1 1 0 2 1 ( ) x e x e x F x x x 3．设随机变量 X 和Y 相互独立，且 ~ ( , ), ~ ( , ) 2 2 2 2 X N m1 s1 Y N m s ，则 Z = X + Y 服从（ ） 学 生 班 级 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 学 生 学 号：□ □ □ □ □ □ □ □ □ □ □ □ 学 生 姓 名：_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ . . . . . . 装 订 线 . . . 装 订 线 . . . 装 订 线 . . . . 试 卷 须 与 答 题 纸 一 并 交 监 考 教 师 . . . . 装 订 线 . . . 装 订 线 . . . 装 订 线 . . . . .

(A) Z~N(μ1,0?+o))(B) Z~N(μ, +μ2,0,,)(C) Z~N(μ, +μ2,o +o)(D) Z~ N(μ) +μ2,002))4.设离散型随机变量X的分布律为P(X=k)=ba*,(k=1,2,..)且b>0，则α为（11(A) ^=(B)=b+1b-1（C）入>0的任意实数(D)2=b+15.已知随机变量X服从二项分布，且E(X)=2.4,D(X)=1.44，则二项分布的参数n,p的值为（(A) n=4, p=0.6(B) n=6,p=0.4(C) n=8, p=0.3(D) n=24, p=0.16.设X,X,,,X是总体X~N(0,1)的简单随机样本，X,S分别是样本的均值和样本标)准差，则有（(A) nX~ N(0,1)(B) X~ N(0,1)(C) 2x? ~ x(n)(D) X~ t(n-1)i=1二、填空题（共11空，每空2分，共22分）1.一批产品共有10个正品2个次品，任意抽取两次，每次抽一个，抽出后不放回，则第二次抽出的是次品的概率为P(A+B)=2. 设AC B, P(A)=0.1, P(B)=0.5,则 P(AB)=_P(A+B)=P(A|B) =3.若随机变量K在(1,6)上服从均匀分布，则方程x2+Kx+1=0有实根的概率是4.如果X，Y的联合分布律用下列表格给出(x,Y)(1, 1)(1, 2)(1, 3)(2, 1)(2, 2)(2, 3)Pα%%YsYβ

（A） ~ ( , ) 2 2 2 Z N m1 s1 + s （B） ~ ( , ) Z N m1 + m2 s1s 2 （C） ~ ( , ) 2 2 2 Z N m1 + m2 s1 +s （D） ~ ( , ) 2 2 2 Z N m1 + m2 s1s 4．设离散型随机变量 X 的分布律为 P(X = k) = b , (k = 1, 2,L) k l 且b > 0，则l 为（ ） （A） 1 1 + = b l （B） 1 1 - = b l （C）l > 0 的任意实数 （D）l = b +1 5.已知随机变量 X 服从二项分布，且 E(X ) = 2.4, D(X ) = 1.44，则二项分布的参数n, p 的 值为（ ） （A）n = 4, p = 0.6 （B）n = 6, p = 0.4 （C）n = 8, p = 0.3 （D）n = 24, p = 0.1 6.设 X X Xn , , , 1 2 L 是总体 X ~ N(0,1)的简单随机样本，X , S 分别是样本的均值和样本标 准差，则有（ ） （A）nX ~ N(0,1) （B） X ~ N(0,1) （C） ~ ( ) 2 1 2 X n n i å i c = （D） ~ t (n -1) S X 二、填空题（共 11 空，每空 2 分，共 22 分） 1.一批产品共有 10 个正品 2 个次品，任意抽取两次，每次抽一个，抽出后不放回，则 第二次抽出的是次品的概率为 . 2.设 A Ì B, P(A) = 0.1, P(B) = 0.5，则 P(AB) = P(A + B) = P(A + B) = P(A | B) = . 3.若随机变量 K 在(1, 6)上服从均匀分布，则方程 1 0 2 x + Kx + = 有实根的概率是 . 4.如果 X ，Y 的联合分布律用下列表格给出 (X,Y) (1, 1) (1, 2) (1, 3) (2, 1) (2, 2) (2, 3) P 6 1 9 1 18 1 3 1 a b

.X与Y相互独立，则α=-x+2x-1，则X的数学期室5.已知连续型随机变量X的概率密度为f(x）=V元E(X)=，X的方差 D(X)=第6.若X,X..X,是取自正态总体X～N(u,)的一个样本，则X=！x,服从.n-三、设某工厂有A,B,C三个车间生产同一型号的螺钉，每个车间的产量分别占该厂螺钉总产量的25%，35%，40%，每个车间成品中的次品分别为各车间产量的5%，4%，2%，如果从全厂总产品中抽取一件产品螺钉为（10分）次品，问它是A车间生产的概率。Ce-(3x+4), x>0, y>0四、设二维随机变量(X,Y)的概率密度为f(x,y)=其他试求（1）常数C；（2）联合分布函数F(xy各煮平煮(18分）(3) P(0<X≤1,0<Y≤2).·.*.以|<x,0<x<1五、设随机变量(x,Y)的概率密度为f(x.y)其他0,（12分）求E(x)。 E(y), cov(X,y)游班毛煮六、某单位设置一总机，共有200个电话分机，设每个电话分机有5%的时间要使用外线电话，假设每个分机是否使用外线通话是互相独立的

X 与Y 相互独立，则a = b = . 5.已知连续型随机变量 X 的概率密度为 ( ) 2 1 1 2 - + - = x x f x e p ，则 X 的数学期望 E(X ) = ， X 的方差 D(X ) = . 6.若 X X Xn , ,., 1 2 是取自正态总体 ( ) 2 X ~ N m,s 的一个样本，则 å= = n i Xi n X 1 1 服从 . 三、设某工厂有 A, B, C 三个车间生产同一型号的螺钉，每个车间的产量分 别占该厂螺钉总产量的 25%，35%，40%,每个车间成品中的次品分别为 各车间产量的 5%，4%，2%，如果从全厂总产品中抽取一件产品螺钉为 次品，问它是 A 车间生产的概率。 （10 分） 四、设二维随机变量(X ,Y )的概率密度为 ( ) ( ) î í ì > > = - + ， 其他 ， 0 0, 0 , 3 4 Ce x y f x y x y 试求（1）常数C ；（2）联合分布函数 F(x, y) （3） P{0 < X Y £1, 0 2 < £ } （18 分） 五、设随机变量(X ,Y )的概率密度为 ( ) î í ì < < < = ， 其他 ， 0 1 , 0 1 , y x x f x y 求 E(X ), E(Y ), cov(X ,Y ) （12 分） 六、某单位设置一总机，共有 200 个电话分机，设每个电话分机有 5%的时 间要使用外线电话，假设每个分机是否使用外线通话是互相独立的， 学 生 班 级 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 学 生 学 号：□ □ □ □ □ □ □ □ □ □ □ □ 学 生 姓 名：_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ . . . . . . 装 订 线 . . . 装 订 线 . . . 装 订 线 . . . . 试 卷 须 与 答 题 纸 一 并 交 监 考 教 师 . . . . 装 订 线 . . . 装 订 线 . . . 装 订 线 . . . . .

问总机要多少外线才能以90%的概率保证每个分机要使用外线时可供使用.(10分）注：Φ(1.28)=0.90[(0+1)x,0<x<1七、设总体X的概率密度为F(x)=，其中-1是未知参数，0其他X，X,，,X，是来自总体X的一个样本容量为n的简单随机样本，求e的极大似然估计值，（10分）

问总机要多少外线才能以 90%的概率保证每个分机要使用外线时可供使用. （10 分） 注：F(1.28) = 0.90 七、设总体 X 的概率密度为 ( ) ( ) î í ì + -1 是未知参数， X X Xn , , 1， 2 L 是来自总体 X 的一个样本容量为n 的简单随机样本，求q 的极大似然 估计值. （10 分）