《概率论与数理统计》课程教学课件(PPT讲稿)第五章 随机变量的数字特征 5.3 协方差与相关系数

5.3协方差与相关系数一、协方差1.定义:对于二维随机变量(X,Y),若E[(X-EX)(Y-EY)存在,则把它称为随机变量X与Y的协方差,记为Cov(X,Y), 即 Cov= E[(X - EX)(Y - EY)] 2.说明:(1) 计算Cov(X,Y)= E(XY)-(EX)(EY)(2)X 与Y相互独立=→Cov(X,Y)=0
5.3 协方差与相关系数 一、协方差 1.定义:对于二维随机变量(X,Y),若E(X − EX)(Y − EY) 存在,则把它称为随机变量 X 与Y 的协方差,记为 Cov(X,Y),即Cov = E(X − EX)(Y − EY)。 2.说明: (1)计算 Cov(X,Y) = E(XY) − (EX)(EY) (2) X 与 Y 相互独立 Cov(X,Y) = 0

3.性质Cov(X,Y)= E[(X- EX)(Y - EY)]设,b是常数,则以下所遇期望和协方差存在时,有1 Cov(a,X) = 0;2 Cov(X,X) = DX;3 Cov(X,Y) = Cov(Y,X);4 Cov(aX,bY) = abCov(X,Y):5 Cov(X + Y,Z) = Cov(X,Z)+Cov(Y,Z)例1设X为一随机变量,其方差为DX,Y=a+bX其中a与b均为常数,求Cov(X,Y)解 Cov(X,Y)= Cov(a +bX,X)= Cov(a,X) + bCov(X,X)= bDX
设a b, , , 是常数 则以下所遇期望和协方差存在时 有 3.性质 1 Cov( , ) 0; a X = 2 Cov( , ) ; X X DX = 3 Cov( , ) Cov( , ); X Y Y X = 4 Cov( , ) Cov( , ); aX bY ab X Y = 5 Cov( , ) Cov( , ) Cov( , ). X Y Z X Z Y Z + = + 例1 设X为一随机变量, 其方差为DX, Y=a+bX, 其中a与b均为常数, 求Cov( X ,Y ). 解 Cov( , ) Cov( , ) X Y a bX X = + = + Cov( , ) Cov( , ) a X b X X = bDX Cov( , ) ( )( ) X Y E X EX Y EY = − −

随机变量的线性逼近与相关系数1.线性逼近:设随机变量x与Y:DX>0,DY>0,若以函数a+bX近似表示Y,以下用误差r=E[Y-a+bX)P来考察这种逼近的好坏程度。推导:r=EY?+α2+b?EX?+2abEX-2aEY-2bE(XY)[r =2a+2bEX-2EY =0[b- Cov(x,n)daDX得AorCov(X,Y)a=EY-bEX-EY=2bEX2+2aEX-2E(XY)=0EXabDXCov(X,Y)Cov(X,Y)DY代入r中,得rmn=PxYDXDYVDXDY则rmin =(1-P)DY
二、随机变量的线性逼近与相关系数 1.线性逼近:设随机变量X 与Y :DX 0, DY 0,若以函数a +bX 近似表示Y ,以下用误差 ( ) 2 r = E Y − a + bX 来考察这种逼近的好坏程 度。 推导: 2 2 2 ( ) 2 2 2 2 r = EY + a + b EX + abEX − aEY − bE XY 令 = + − = = + − = 2 2 2 ( ) 0 2 2 2 0 2 bEX aEX E XY b r a bEX EY a r 得 = − = − = EX DX Cov X Y a EY bEX EY DX Cov X Y b ( , ) ( , ) 代入 r 中,得 DY DX DY Cov X Y r = − 2 min ( , ) 1 令 ( ) DX DY Cov X Y XY , = 则 r (1 XY )DY 2 min = −

Cov(x,y)2. 定义:把上述无量纲的量p=微称为随机变量X与Y的(线性)相关系数。3.相关系数的性质:定理5.3. 1(1)lPx≤1(2)[Pxr|=1存在常数a,b使P(Y=a+bX)=1证明 Pxy =±1rmin =0 3a,b使E[Y-(α+bX)=0- D[Y - (a + bX)]+ (E[Y - (a+ bx) = 0[D[Y - (a +bX)]= 03a,b使E[Y - (a+ bx)]= 0 3a,b使P(Y = a+bX}= 1即X与Y之间以概率1存在着线性关系
2.定义:把上述无量纲的量 ( ) DX DY Cov X Y XY , = 称为随机变量 X 与Y 的(线性)相关系数。 3.相关系数的性质: 定理 5.3.1(1) XY 1 (2) XY =1存在常数a,b使 PY = a + bX=1 证明 XY = 1 r min = 0 , [ ( )] 0 2 a b使E Y − a + bX = ( ) ( ) 0 2 D Y − a + bX + E Y − a + bX = ( ) ( ) − + = − + = 0 0 , E Y a bX D Y a bX a b使 a,b使PY = a + bX=1 即 X 与 Y 之间以概率 1 存在着线性关系

说明:(1)Px刻画了X与Y的(线性)相关性:lpxrl越小,rmin 越大,即X与Y的线性关系较差,反之较好;当Px=0时称X与Y不相关。(2)相互独立与不相关:一般地,X与Y相互独立时一定不相关。但X与Y不相关时不一定相互独立(见例 2)。特殊的,当(X,Y)服从二维正态分布时,X与Y不相关等价于二者相互独立
说明: (1) xy 刻画了 X 与 Y 的(线性)相关性: XY 越 小, min r 越大,即 X 与Y 的线性关系较差,反之较 好;当 xy = 0时称 X 与Y 不相关。 (2)相互独立与不相关:一般地, X 与Y 相互独 立时一定不相关 。但 X 与Y 不相关时不一定相互 独立(见例 2)。特殊的,当(X,Y)服从二维正态分 布时, X 与Y 不相关等价于二者相互独立
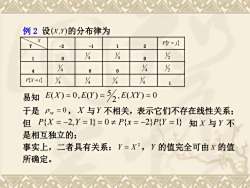
例 2设(X,Y)的分布律为P(Y =j)-12Y1-2Y4Y4Y010Y4Y4Y040Y44Y44P(X =i)1E(X)= 0,E(Y)= 5,E(XY) = 0易知于是P=0,X与Y不相关,表示它们不存在线性关系;但 P[X=-2,Y=1)=0± P(x=-2)P(Y=1) 知 X 与 Y 不是相互独立的;事实上,二者具有关系:Y=X2,Y的值完全可由X的值所确定
例 2 设(X,Y)的分布律为 X Y -2 -1 1 2 PY = j 1 0 4 1 4 1 0 2 1 4 4 1 0 0 4 1 2 1 PX = i 4 1 4 1 4 1 4 1 1 易知 , ( ) 0 2 5 E(X) = 0,E(Y) = E XY = 于是 xy = 0, X 与Y 不相关,表示它们不存在线性关系; 但 P{X = −2,Y = 1} = 0 P{x = −2}P{Y = 1} 知 X 与 Y 不 是相互独立的; 事实上,二者具有关系: 2 Y = X ,Y 的值完全可由 X 的值 所确定
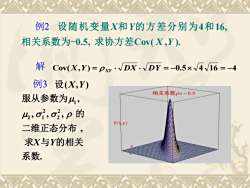
例2设随机变量X和Y的方差分别为4和16相关系数为-0.5,求协方差Cov(X,Y)解Cov(X,Y) = Pxy : DX . VDY = -0.5× V4 /16 = -4例3 设(X,Y)相关系数p=-0.9服从参数为μ,M,0,o2,p 的f(x,y)二维正态分布,求X与Y的相关系数
设随机变量X和Y的方差分别为4和16, 相关系数为-0.5, 求协方差Cov( X ,Y ). 例2 解 Cov(X,Y ) = XY D X D Y = −0.5 4 16 = −4 1 2 2 2 1 2 ( , ) , , , . X Y X Y 设 服从参数为 的 二维正态分布 求 与 的相关 系数 例3

exp(h)例3 解二维正态分布的密度是f=2元0,02 /1-p(x-μ)?(x-u)(y-μ)+(y-μ,)-2ph2(1-p292a0,02t?+uu+2udxdy(x-μ,)(y-μ,)ehCov(X,Y)0,02 /1-pt'+u?1(o,u)o2(pu+t /1-p2)edtdu2T0
例3 解 2 2 1 2 1 exp( ) σ σ ρ h f − = − + − − − − − − = 2 2 2 2 1 2 1 2 2 1 2 1 2 ( )( ) ( ) 2 ( ) 2(1 ) 1 σ y μ σ σ x μ y μ ρ σ x μ ρ h t u 2 1 2 1 2 1 d d ( )( )e 2 1 Cov( , ) σ σ ρ x y X Y x μ y μ h − = − − − − 二维正态分布的密度是 σ u σ u t ρ t u t u ( ) ( 1 )e d d 2 1 2 2 1 2 2 2 + − − − = + − 0 2 2 2 t + u = − − + − − − − = − 2 1 1 2 1 1 2 2 2 1 1 2 1 σ x μ σ x μ ρ σ y μ

?+u?( (czpu')e2dtduCov(X,Y)-2元2du=002p=0.02元Cov(X,Y)002P所以Pxy=(DX = 0, DY = 0)OJDXJDY0102参数p就是X与Y的相关系对于二维正态分布,数,因而二维正态分布可由X与Y的期望、方差及它们的相关系数完全确定.且有如下关系:不相关相互独立参数p=0
对于二维正态分布, 参数ρ就是X与Y 的相关系 数, 因而二维正态分布可由X与Y 的期望、方差及 它们的相关系数完全确定. 且有如下 X Y σ σ u t u t u ( )e d d 2 1 Cov( , ) 2 2 1 2 2 2 + − − − = + − + − − − = σ σ t u u t u e d 2 1 e d 2 1 2 2 2 1 2 2 2 = σ1 σ2 关系: = = = 1 2 1 2 Cov( , ) σ σ σ σ DX DY X Y 所以 XY ( , ) 2 2 2 DX = σ1 DY = σ 相互独立 参数ρ=0 不相关
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《概率论与数理统计》课程教学课件(PPT讲稿)第五章 随机变量的数字特征 5.1 数学期望.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第四章 随机变量及其数值模拟 4.2 二维随机变量函数的分布.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第五章 随机变量的数字特征 5.2 方差.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第四章 随机变量及其数值模拟 4.1 一维随机变量函数的分布.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第三章 随机向量及其分布 3.3 条件分布.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第三章 随机向量及其分布 3.4 随机变量的独立性.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第三章 随机向量及其分布 3.2 边缘分布.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第三章 随机向量及其分布 3.1 二维随机变量的概率分布.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第二章 随机变量及其分布 2.2 离散型随机变量的概率分布.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第二章 随机变量及其分布 2.3 连续型随机变量的概率分布.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第二章 随机变量及其分布 2.1 随机变量与分布函数.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第一章 随机事件及其概率 1.5 随机事件的独立性.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第一章 随机事件及其概率 1.1 样本空间与随机事件.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第一章 随机事件及其概率 1.2 事件的频率与概率.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第一章 随机事件及其概率 1.3 古典概型与几何概型.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第一章 随机事件及其概率 1.4 条件概率.ppt
- 《概率论与数理统计》课程教学资源(试卷习题)2009-2010学年第一学期考试试题(题目).pdf
- 《概率论与数理统计》课程教学资源(试卷习题)2008-2009学年第一学期考试试题(题目).pdf
- 《概率论与数理统计》课程教学资源(试卷习题)2009-2010学年第一学期考试试题(答案).pdf
- 《概率论与数理统计》课程教学资源(试卷习题)2008-2009学年第一学期考试试题(答案).pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第五章 随机变量的数字特征 5.4 原点矩与中心矩.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第六章 大数定律和中心极限定理 6.2 中心极限定理.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第六章 大数定律和中心极限定理 6.1 大数定律.ppt
- 《复变函数与积分变换》课程教学大纲 Complex Function and Integral Transformation.pdf
- 《复变函数与积分变换》课程考试大纲 Complex Function and Integral Transformation.pdf
- 《复变函数与积分变换》课程教学资源(教材讲义)第三章 复变函数的积分.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第四章 解析函数的级数表示.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第二章 解析函数.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第一章 复数与复变函数.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第七章 解析函数在平面场的应用.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第五章 留数及其应用.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第六章 共形映射.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第八章 傅里叶变换.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第九章 拉普拉斯变换.doc
- 《复变函数与积分变换》课程教学资源(PPT课件)第一章 复数与复变函数 1.6 第六节 复变函数的极限和连续性.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第一章 复数与复变函数 1.5 第五节 复变函数.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第一章 复数与复变函数 1.0 习题课.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第一章 复数与复变函数 1.4 第四节 区域.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第一章 复数与复变函数 1.1 第一节 复数及其代数运算.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第一章 复数与复变函数 1.3 第三节 复数的乘幂与方根.ppt
