《概率论与数理统计》课程教学课件（PPT讲稿）第六章 大数定律和中心极限定理 6.1 大数定律

第六章大数定律与中心极限定理大数定律6.16.2中心极限定理

6.1 大数定律 6.2 中心极限定理 第六章 大数定律与中心极限定理

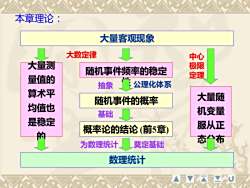
本章理论：大量客观现象大数定律中心大量测极限随机事件频率的稳定定理量值的公理化体系抽象算术平大量随随机事件的概率均值也机变量基础是稳定服从正概率论的结论（前5章）的态台布奠定基础为数理统计数理统计

本章理论： 随机事件的概率 随机事件频率的稳定 性 大量客观现象 概率论的结论 (前5章) 公理化体系 大数定律 抽象 基础 大量测 量值的 算术平 均值也 是稳定 的 大量随 机变量 服从正 态分布 中心 极限 定理 数理统计 为数理统计 奠定基础

大数定律6.1大数定律#是概率论中用来阐明大量随机现象平均结果稳定性和事件频率稳定性的一系列定理

是概率论中用来阐明大量随机现象平均 结果稳定性和事件频率稳定性的一系列定理 大数定律 6.1 大数定律

引理1（切比雪夫不等式）设随机变量X有数学期望EX及方差DX,则对V>0,有DXP((X - EX|≥8)≤（切比雪夫不等式）28或DXP[x-EX|<6}≥1（切比雪夫不等式）证（只就连续型证明）设密度为f(α),则有[x-EX]?P(Ix-EX|≥6)={f(x)dx ≤f(x)dx3[x-EX|≥81x-EX/28DX(**(x- EX)" f(x)dx

引理1   2 1   DX P X − EX   − （切比雪夫不等式）设随机变量X 有数学期望EX 或 及方差DX, 则 对  0,有   2   DX P X − EX   证（只就连续型证明）设密度为f (x), 则有    −  −  =   x EX P X EX f (x)d x  −  −    x EX f x x x EX ( )d 2 2  +  −  (x − EX) f (x)d x 1 2 2  2  DX = （切比雪夫不等式） （切比雪夫不等式）

定理1（切比雪夫大数定律）设X，X.相互独立且分别有数学期望EX,及有公共上界的方差DX,≤K(k=1,2,)作算术平均值Y=1X,则对V>0,有ni=llim P([Y, - EY,|或Y.-EY.P>0(n→0)(称Y.一EY.依概率收敛于O)宏EEX其中EY=切比雪夫大数定律以严格的数学形式表明：随着n的增大，大量随机变量的算术平均值Y，稳定于它的期望值EY

lim  −  = 1 →  n n n P Y EY 定理1 （切比雪夫大数定律） 设X1 , X2 , . 相互独立且 其中 分别有数学期望EXi 及有公共上界的方差 ( 1,2, ) DX K k i  = 1 1 n n i i Y X n = 作算术平均值 =  ,则 Y − EY ⎯→0 (n → ) P n n 或 ( 0) 称Y EY n n − 依概率收敛于 1 1 n n i i EY EX n = =  对   0,有 切比雪夫大数定律以严格的数学形式表明：随着n的增 大, 大量随机变量的算术平均值Yn稳定于它的期望值EYn

证明这时，对任意的正整数n，有KEY, =-ZEX, DY, =-ZDX, ≤Y故由切比雪夫不等式知，对Vε>0,有KDY.>1P[ [Y, -EY,|00,即知 lim P[Y,-EY,|<}=1如果把定理1中的X看成n重伯努利试验中第i次试验时A发生的次数（即X，服从0-1分布）并记P(A)=P，则EX, = p, DX, = p(1-p), Y, --2x, - ", EY, = p于是定理1可表现为如下的定理2的形式

证明   2 1 n n n DY P Y EY   −   − lim  −  = 1 →  n n n P Y EY 故由切比雪夫不等式知,对   0,有 2 1 1 1 1 n n n i n i i i K EY EX DY DX n n = = n = =    ， 这时,对任意的正整数n, 有 2 1 n K  − 令n→,即知 如果把定理1中的Xi看成 n重伯努利试验中第 i 次试验 时A发生的次数（即Xi 服从0-1分布）并记 P(A)=p, 则 , 1 1 n n X n Y A n k n =  k = = EX p DX p p i i = = − , (1 ) , EY p n = 于是定理1可表现为如下的定理 2的形式

（伯努利大数定律）定理2设n是n重伯努利试验中A发生的次数,p=P(A),则对Vε>0,有limPn-0或A.nsPp(n→0)(称频率依概率收敛于p)nn伯努利大数定律以严格的数学形式表明：当试验在不变的条件下重复进行很多次时，事件的频率稳定于它的概率因此，在实际应用中可用频率代替概率，这也为概率的公理化定义提供了理论支持

定理2 lim = 1       −  → p  n n P A n （伯努利大数定律）设nA是n重伯努利试验中A 发生的次数, p=P(A), 则对  0,有 ⎯→ p (n → ) n nA P 或 ( ) nA p n 称频率 依概率收敛于 伯努利大数定律以严格的数学形式表明：当试验在不 变的条件下重复进行很多次时, 事件的频率稳定于它的概率. 因此, 在实际应用中可用频率代替概率. 这也为概率的公理化 定义提供了理论支持

由伯努利大数定律可知，如果事件A的概率很小，则事件A发生的频率也很小，因此，在实际问题中我们常采用实际推断原理（小概率事件的实际不可能原理）概率很小的事件在个别试验中几乎是不会发生的概率很大的事件在个别试验中几乎一定会发生如果概率很小的事件在一次试验中竟然发生了，那我们就有理由怀疑“概率很小”这一假定的正确性当然，无论事件概率多么小，总是可能发生的。因此所谓小概率事件的实际不可能原理仅仅适用于个别的或次数极少的试验，当试验次数较多时就不适用了

概率很小的事件在个别试验中几乎是不会发生的 概率很大的事件在个别试验中几乎一定会发生 实际推断原理（小概率事件的实际不可能原理） 由伯努利大数定律可知，如果事件A的概率很小, 则事 件A发生的频率也很小. 因此, 在实际问题中我们常采用 如果概率很小的事件在一次试验中竟然发生了，那 我们就有理由怀疑“概率很小”这一假定的正确性． 当然,无论事件概率多么小, 总是可能发生的. 因此, 所谓小概率事件的实际不可能原理仅仅适用于个别的或 次数极少的试验,当试验次数较多时就不适用了．

定理3（辛钦大数定律）设随机变量序列X，相互独立,服从同一分布,且E(X,)=μ，则对任意的ε>0,有P含x,-00或X=1Zx,Pμ (n→o)M辛钦大数定律以严格的数学形式表明：当n无限增大时，独立同分布的随机变量的平均值依概率收敛于它的期望.这为数理统计的矩估计奠定了理论基础

1 1 lim 1 =        −  = →   n i i n X n P 定理3（辛钦大数定律）设随机变量序列{Xn }相互独 立, 服从同一分布,且 E( Xn )= , 则对任意的ε>0 , 有 ( ) 1 1 =  ⎯→ →  = X n n X P n i i  或 辛钦大数定律以严格的数学形式表明：当n无限增大 时, 独立同分布的随机变量的平均值依概率收敛于它的期 望. 这为数理统计的矩估计奠定了理论基础

Xx>0用切比雪夫不等式证明例1 设X~ f(x)=n!0,x≤0,nP0<X<2(n+1))≥n+1torx+8+00证EX=dxe-*dx=n+1+(n++.n!n!n!七+21+1t0100+oEX2e-*dx=(n+1)(n+2)dxfin-.n!n!n!所以 DX = EX2 -(EX) =(n+2)(n+1)-(n+1)= n+1从而 P(0<X<2(n+1)=P(l X-EX<n+1)n+1n(这里=n+1)≥1(n+1)n+1

例1 设X~ , 0, ( ) ! 0 , 0, n x x e x f x n x −    =     用切比雪夫不等式证明 1 {0 2( 1)} +   +  n n P X n 证 0 e d ! n x x EX x x n + − =  2 2 0 e d ! n x x EX x x n + − =  所以 P{0  X  2(n +1)} = P{| X − EX | n +1} 2 ( 1) 1 1 + +  − n n + 1 = n n 2 2 2 DX EX EX n n n = − = + + − + ( ) ( 2)( 1) ( 1) = n+1 = (n + 1)(n + 2) (这里 = + n 1) 1 0 0 e ( 1) e d ! ! n n x x x x n x n n + + + − − = − + +  2 1 0 0 e ( 2) e d ! ! n n x x x x n x n n + + + + − − = − + +  = n+1 从而