《概率论与数理统计》课程教学课件(PPT讲稿)第二章 随机变量及其分布 2.2 离散型随机变量的概率分布

1.2离散型随机变量的概率分布一.离散型随机变量及分布律定义1.定义:如果随机变量X仅可能取有限个或可列无限多个值,则称X为离散型随机变量
1.2 离散型随机变量的概率分布 一.离散型随机变量及分布律定义: 1.定义:如果随机变量 X 仅可能取有限个或可列 无限多个值,则称 X 为离散型随机变量.

2.定义:设离散型随机变量X的所有可能的取值为x,(k =1,2,),x 取各个可能值的概率为P(X = x,) = Pk, (k = 1,2,..) (2.1)由概率的定义,P,满足如下两个条件1° pk ≥ 0, (k =1,2,...) (2.2)人2°Z=1(2.3)Pkk=1称(2.1)式为离散型随机变量 X的分布律
2 1 (2.3) 1 0, ( 1,2, ) (2.2) 1 0 0 = = k= k k p p k 2.定义:设离散型随机变量 X 的所有可能的取值 为 x (k = 1,2, ), k X 取各个可能值的概率为 PX = x = p , (k = 1,2, ) (2.1) k k 由概率的定义, pk满足如下两个条件 称(2.1)式为离散型随机变量 X 的分布律
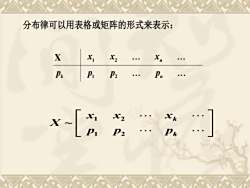
分布律可以用表格或矩阵的形式来表示:XxxX1PkPnPiP2xiX2XkX.piP2Pk
分布律可以用表格或矩阵的形式来表示: X x1 x2 xn k p p1 p2 pn k k p p p x x x X 1 2 1 2 ~
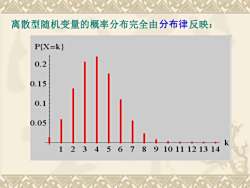
离散型随机变量的概率分布完全由分布律反映P(X-k)0.20.150.10.05112.1314
离散型随机变量的概率分布完全由分布律反映:

二.分布律性质:性质1: pk ≥0,k = 1,2,3...性质2:Zpk=1k=1三.分布率与分布函数间的关系F(x)= P(X≤x) = ZP(X =x}= ZPk;XSxX<xP(X = x) = F(x)- F(x -0)
二.分布律性质: p 0,k 1,2,3,. k = p 1 k 1 k = = 性质1: 性质2: 三.分布率与分布函数间的关系: { } ( ) ( ) ( ) { } { } ; = = − − 0 = = = = k k k x x k x x k P X x F x F x F x P X x P X x p k k

例1:设随机变量X的分布律为X23-1P1/41/41/2求:X的分布函数,并求35P(2 ≤X≤3)PXX22
例1:设随机变量X的分布律为 X -1 2 3 P 1/4 1/2 1/4 求:X的分布函数,并求 }, {2 3}. 2 5 2 3 }, { 2 1 P{X P X P X

例2袋中有2个白球和3个黑球,每次从袋中任取1个球,直至取得白球为止,若每次取出的黑球不再放回去,求取球次数X的分布律解:X的所有可能取值是12.3.4.由古典概型易知223= 0.4PX =0.3P(X =:1721三15-3222321P(X =0.237=P(X =0.14754.33AX342故X的分布律为:0.20.40.30.1Pk
袋中有2个白球和3个黑球,每次从袋中任 取1个球,直至取得白球为止,若每次取出的黑球 不再放回去,求取球次数X 的分布律. 例2 解: X 的所有可能取值是1, 2, 3, 4.由古典概 型易知 X 1 2 3 4 pk 0.4 0.3 0.2 0.1 0.4 5 2 P{X = 1} = = 0.3 4 2 5 3 P{X = 2} = = 0.2 3 2 4 2 5 3 P{X = 3} = = 0.1 2 2 3 1 4 2 5 3 P{X = 4} = = 故X的分布律为:

例3袋中有2个白球和3个黑球,每次从袋中任取1个球,直至取得白球为止,若每次取出的黑球仍放回去,求取球次数X的分布律解因为取出的黑球仍放回去,所以X的所有可能取值是1.2.·.故由相互独立的乘法定理可知几何分布X的分布律为:Xk120.40.4×0.6k-10.4x0.6Pk(6)其中= 0.4× 0.6k-1, k = 1,2,P(X = k) =
袋中有2个白球和3个黑球,每次从袋中任 取1个球,直至取得白球为止,若每次取出的黑球 仍放回去,求取球次数X 的分布律. 例3 解 因为取出的黑球仍放回去,所以X的所有 可能取值是1,2,···. 故由相互独立的乘法定理可知 X的分布律为: 0.4 0.6 , 1,2, 5 3 5 2 { } 1 1 = = = = − − P X k k k k X 1 2 ··· k ··· pk 0.4 0.40.6 ··· 0.40.6k-1 ··· 几何分布 其中

几何分布的一般形式为:23Xkpq3pqkpq2pqlPkp
几何分布的一般形式为: X 1 2 3 4 . k . pk p pq1 pq2 pq3 . pqk

四.常用离散型随机变量的分布0-1分布设随机变量X只可能取a与b两个值(不失一般性,总可以取a=0,b=1),其概率分别为(1-p)和p,则X的概率分布为称该分布为0-1分布或两点分布,记作X~(0,1)
四.常用离散型随机变量的分布 0-1分布 设随机变量 X 只可能取a与b两个值(不失一 般性, 总可以取a=0, b=1), 其概率分别为(1-p) 和p, 则 X 的概率分布为 0 1 ~ 1 X p p − 称该分布为0-1分布或两点分布, 记作X~(0, 1)
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《概率论与数理统计》课程教学课件(PPT讲稿)第二章 随机变量及其分布 2.3 连续型随机变量的概率分布.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第二章 随机变量及其分布 2.1 随机变量与分布函数.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第一章 随机事件及其概率 1.5 随机事件的独立性.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第一章 随机事件及其概率 1.1 样本空间与随机事件.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第一章 随机事件及其概率 1.2 事件的频率与概率.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第一章 随机事件及其概率 1.3 古典概型与几何概型.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第一章 随机事件及其概率 1.4 条件概率.ppt
- 《概率论与数理统计》课程教学资源(试卷习题)2009-2010学年第一学期考试试题(题目).pdf
- 《概率论与数理统计》课程教学资源(试卷习题)2008-2009学年第一学期考试试题(题目).pdf
- 《概率论与数理统计》课程教学资源(试卷习题)2009-2010学年第一学期考试试题(答案).pdf
- 《概率论与数理统计》课程教学资源(试卷习题)2008-2009学年第一学期考试试题(答案).pdf
- 《概率论与数理统计》课程教学资源(试卷习题)2007-2008学年第一学期考试试题(题目).pdf
- 《概率论与数理统计》课程教学资源(试卷习题)2006-2007学年第一学期考试试题(题目).pdf
- 《概率论与数理统计》课程教学资源(试卷习题)2007-2008学年第一学期考试试题(答案).pdf
- 《概率论与数理统计》课程教学资源(试卷习题)2006-2007学年第一学期考试试题(答案).pdf
- 《概率论与数理统计》课程教学资源(电子教案)第5章 随机变量的数字特征.pdf
- 《概率论与数理统计》课程教学资源(电子教案)第4章 随机变量的函数.pdf
- 《概率论与数理统计》课程教学资源(电子教案)第6章 大数定律与中心极限定理.pdf
- 《概率论与数理统计》课程教学资源(电子教案)第3章 随机向量及其分布.pdf
- 《概率论与数理统计》课程教学资源(电子教案)第2章 随机变量及其分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第三章 随机向量及其分布 3.1 二维随机变量的概率分布.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第三章 随机向量及其分布 3.2 边缘分布.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第三章 随机向量及其分布 3.4 随机变量的独立性.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第三章 随机向量及其分布 3.3 条件分布.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第四章 随机变量及其数值模拟 4.1 一维随机变量函数的分布.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第五章 随机变量的数字特征 5.2 方差.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第四章 随机变量及其数值模拟 4.2 二维随机变量函数的分布.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第五章 随机变量的数字特征 5.1 数学期望.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第五章 随机变量的数字特征 5.3 协方差与相关系数.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第五章 随机变量的数字特征 5.4 原点矩与中心矩.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第六章 大数定律和中心极限定理 6.2 中心极限定理.ppt
- 《概率论与数理统计》课程教学课件(PPT讲稿)第六章 大数定律和中心极限定理 6.1 大数定律.ppt
- 《复变函数与积分变换》课程教学大纲 Complex Function and Integral Transformation.pdf
- 《复变函数与积分变换》课程考试大纲 Complex Function and Integral Transformation.pdf
- 《复变函数与积分变换》课程教学资源(教材讲义)第三章 复变函数的积分.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第四章 解析函数的级数表示.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第二章 解析函数.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第一章 复数与复变函数.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第七章 解析函数在平面场的应用.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第五章 留数及其应用.doc
