《概率论与数理统计》课程教学课件（PPT讲稿）第四章 随机变量及其数值模拟 4.2 二维随机变量函数的分布

4.2 二维随机变量函数的分布设(X,Y）是分布已知的二维随机变量，g(x，y)是二元连续函数，那么Z一g(X,Y)就是一个一维随机变量.按定义，随机变量Z=g(X,Y)的分布函数应为Fz(z)=P(Z≤z) =Pig(X,Y)≤z)本节讨论如何由已知的二维随机变量（X,Y的分布去求它的函数 Z=g(X,Y)的分布．特别如函数形式: Z=X±Y,Z=max(X,Y),Z=min(X,Y)

本节讨论如何由已知的二维随机变量(X,Y)的 分布去求它的函数 Z＝g(X,Y)的分布．特别如函 数形式： 设(X,Y )是分布已知的二维随机变量, g(x, y)是 二元连续函数, 那么Z＝g(X,Y)就是一个一维随机变 量. 按定义, 随机变量 Z＝g(X,Y)的分布函数应为 4.2 二维随机变量函数的分布 F (z) P{Z z} P{g(X,Y) z} Z =  =  Z X Y Z X Y Z X Y =  = = , max( , ), min( , )

例1 设(X,Y)的分布律Y0-1X1如右，求X+Y，max(X,Y)0.20.10与min(X,Y)的分布律0.20.10.10.3助

例1 设(X, Y)的分布律 如右, 求X+Y, max(X,Y ) 与min(X,Y )的分布律. Y X －1 0 1 0 0.1 0.2 0.2 1 0.1 0.1 0.3

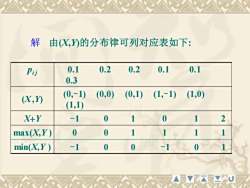
解日由(X,Y)的分布律可列对应表如下：0.20.10.20.10.1Pij0.3(0,0)(0,1)(1,0)(0,-1)(1,-1)(X,n)(1,1)0X+Y-1020011max(X,Y)0-10min(X,Y)1动

由(X,Y)的分布律可列对应表如下: pi j 0.1 0.2 0.2 0.1 0.1 0.3 (X,Y) (0,-1) (0,0) (0,1) (1,-1) (1,0) (1,1) X+Y -1 0 1 0 1 2 max(X,Y ) 0 0 1 1 1 1 min(X,Y ) -1 0 0 -1 0 1 解

将函数的所有可能取值重排并概率即可得分布律02X+Y0.10.30.30.30max(X,Y)0.30.701-1min(X,Y)0.20.50.3

分布律      − 0.2 0.5 0.3 1 0 1 min( X,Y ) ~       0.3 0.7 0 1 max( X,Y ) ~      − + 0.1 0.3 0.3 0.3 1 0 1 2 X Y ~ 将函数的所有可能取值重排并概率即可得

例2设两个独立的随机变量X与Y的分布律为3241YXp.jPi.0.30.70.60.4求随机变量Z-X+Y的分布律解 因X与Y独立,所以 P(X=X,Y=y;}= Pi。PijP(X=X,Y =y;}0.180.120.420.28(X,Y)(1, 2)(1, 4)(3, 2)(3, 4)3557Z=X+Y537Z=X+Y所求分布律P(Z = zk)0.540.180.28U

设两个独立的随机变量X 与Y 的分布律为 求随机变量 Z=X+Y 的分布律. i j i j P X x Y y p p • • 解 因X与Y 独立, 所以 { = , = } =  例2 X pi• 1 3 0.3 0.7 Y 2 4 j 0.6 0.4 p• (X,Y ) 0.18 0.12 0.42 0.28 Z = X +Y 3 5 5 7 Z = X +Y { }k P Z = z 3 5 7 0.18 0.54 0.28 所求分布律： { , } i j P X = x Y = y (1, 2) (1, 4) (3, 2) (3, 4)

连续型随机变量函数的分布1）Z=X+Y的分布设(X,Y)的密度为f(x,),则Z = X +Y 的分布函数为Fz(z) = P(Z≤z)= [J f(x,y)dxd yx+ySzx+y=z=J-"*f(x,y)dyl dxy=t-x " f(x, -x)dtjdx0=J"1ft f(x,t -x)dx]dt+8同理故fz(z)=" f(x,z-x)dxf(z-y,y)d j动

设( , ) ( , ), X Y f x y Z X Y 的密度为 则 = + 的分布函数为 F (z) P{Z z} Z =  f x y x y x y z ( , )d d  +  = x y O x + y = z [ ( , )d ] d z x f x y y x + − − − =   y = t − x [ ( , )d ]d z f x t x t x + − − −   [ ( , )d ]d z f x t x x t + − − = −   1) Z=X+Y 的分布 故 ( ) ( , )d Z f z f x z x x + − = −  f z y y y ( , )d + − −  同理 连续型随机变量函数的分布

当X,Y独立时，fz(z)也可表示为fz(z)= / fx(x)fr(z-x)dxfz(z)= x(z-y)fr(y)dy其中fx(x),f(y)分别为(X,Y)的两个边缘分布密度例3设X和Y是两个相互独立的随机变量，分布密度分别为e-,y>o[1, x e (0,1)fr(y) =和fx(x)=[0, 其它0,其它求其和Z=X十Y的分布密度

当 X, Y 独立时, f Z (z)也可表示为  + − f z = f z − y f y y Z ( ) X ( ) Y ( )d f z f x f z x x Z ( ) X ( ) Y ( )d  + − = − 其中 f (x), f ( y)分别为(X,Y)的两个边缘分布密度. X Y     = 0, 其 它 1, (0,1) ( ) x f x X 例3 设X和Y是两个相互独立的随机变量, 分布 密度分别为 和 求其和Z＝X＋Y的分布密度．     = − 0,其它 , 0 ( ) e y f y y Y

由卷积公式知，Z=X十Y的分布密度为fz(2)= / fx(x)fr(z-x)dx0 ≤ z<1时, f:(2)=I'e-()dx=(e-1)e当时, f.(2)=[ie-(=-)dx =1-e-:当当z≥1 z<0 时， 由fx(x)=0知f2(2)=0,1-e-,0≤z≤1(e-l)e-",z ≥1fz)=30,其它

 + − f z = f x f z − x x Z ( ) X ( ) Y ( )d 由卷积公式知, Z＝X＋Y的分布密度为 当 时， 当 时 ， 当 时， 0  z 1 z z z x z f z e dx e − − − = = −  ( ) 1 0 ( ) z  1 z x z z f z e dx e e − − − = = −  ( ) ( 1) 1 0 ( ) f (x) = 0 f (z) = 0, z  0 由 X 知 Z      −  −   = − − 0,其它 ( 1) , 1 1 ,0 1 ( ) e e z e z f z z z z

定理1设XN(u,o),～N(uz,o)且相互独立则Z=X+Y亦服从正态分布，且X+Y~N(u+μ+）证由卷积公式知，Z=X十Y的分布密度为fz(z) = ( fx(x)f(z-x)dx(x-u)(z-x-μ)10dxexp2022022元0,02g+ozo? -μ,0i + u,o2(z -μi - μ2)dxexpx-2元0020102i +o?2(o +02)zo; -H,o + MfC2+0很繁的过=tXio2i+o?程

定理1 ~ ( , ) 2 Y N 2  2 ~ ( , ), 2 设X N 1  1 则Z=X+Y亦服从正态分布, 且 ~ ( , ). 2 2 2 X +Y N μ1 + μ2 σ1 + σ 且相互独立, 证  +  − f Z (z) = f X (x) f Y (z − x)d x 由卷积公式知, Z＝X＋Y 的分布密度为  + −       − − − − = − x σ z x μ σ x μ σ σ d 2 ( ) 2 ( ) exp 2 1 2 2 2 2 2 1 2 1  1 2 ( )  + −         + − − −         + − + − + = − x σ σ z μ μ σ σ zσ μ σ μ σ x σ σ σ σ σ σ d 2 ( ) 2 exp 2 1 2 2 2 1 2 1 2 2 2 2 2 1 2 1 2 2 2 1 2 1 2 2 2 1 2 2 2 1  1 2 t σ σ zσ μ σ μ σ x σ σ σ σ =        + − + − + 2 2 2 1 2 1 2 2 2 1 2 1 2 2 2 1 2 2 2 令 1 很繁的过 程

o+02zoi-o+u02故令0i +020,02fz(z) = /fx(x)fr(z-x)dxZo-2 +02(z-μ-μz+0dxexp1+022(c +02)2元0，020'0201(z-Hi-μ220i+022d/2元./0+0212元(z--2)120+02V2元.0+02所以 X+Y~N(u+μ2, +)

故令  +  − f Z (z) = f X (x) f Y (z − x)d x ( )  + −         + − − −         + − + − + = − x σ σ z μ μ σ σ zσ μ σ μ σ x σ σ σ σ σ σ d 2 ( ) 2 exp 2 1 2 2 2 1 2 1 2 2 2 2 2 1 2 1 2 2 2 1 2 1 2 2 2 1 2 2 2 1  1 2 t σ σ zσ μ σ μ σ x σ σ σ σ =        + − + − + 2 2 2 1 2 1 2 2 2 1 2 1 1 2 2 2 2 1 ( )  + − − + − − −   + = t σ σ t σ σ z μ μ e d 2 1 e 2 1 2 2 ( ) 2 2 2 1 2 2 2 2 1 2 1 2   ( ) 2 2 2 1 2 1 2 2 ( ) 2 2 2 1 e 2 1 σ σ z μ μ σ σ + − − −  + =  ~ ( , ) 2 2 2 所以 X +Y N μ1 + μ2 σ1 + σ