《概率论与数理统计》课程教学课件（PPT讲稿）第一章 随机事件及其概率 1.2 事件的频率与概率

1.2事件的频率与概率事件的频率1定义1：在相同条件下，进行n次试验，事件A发生n次，则称比值"为事件A 发生的频率,记作 f.(A),即 f.(A)="41频率满足下述三条基本性质（非负性）110≤f,(A)≤12、（规范性）f,(Q)=13、（有限可加性）对两两互不相容事件A,A，.,A,有：f.(ZA)-Zf.(A)i=-1i-l(NKD)Probability and Statistics

Probability and Statistics （NKD） 1.2 事件的频率与概率 一、事件的频率 , , , ( ). ( ) A A A n n n A n n n A f A f A n n = 在相同条件下 进行 次试验 事件 发生 次，则 称比值 为事件 发生的频率 记作 即 定义1： 频率满足下述三条基本性质： 0 1 n 1、（非负性）   f ( A ) 2、（规范性） 1 n f ( )  = 3、（有限可加性）对两两互不相容事件 A ,A ,.,A 1 2 n 有： 1 1 n n n i n i i i f ( A ) f ( A ) = =  =

注：频率一定程度上可以表示事件A发生的可能性的大小但由于它的波动性，用其表示事件A发生的可能性（概率）是不合适的，但通过试验我们发现：频率具有稳定性。具体地说：当试验次数n逐渐增大时，频率fn（A）呈现出稳定性例考虑“抛硬币”这个试验，考虑正面发生的事件为A，我们将一枚硬币抛5次，50次，500次，各做10遍，用表示事件A发生的次数f（A）表示A发生的频率，则得到的数据如表1.1所示。这样的试验在历史上也有不少人做过其中最著名的结果见表1.2NKDProbabilityand Statistics

Probability and Statistics （NKD） 注：频率一定程度上可以表示事件A发生的可能性的大小， 但由于它的波动性，用其表示事件A发生的可能性（概率） 是不合适的，但通过试验我们发现：频率具有稳定性。 具体地说：当试验次数n逐渐增大时，频率 f ( A ) n 呈现出稳定性. n f ( A ) A n 例 考虑“抛硬币”这个试验，考虑正面发生的事件为A,我们 将一枚硬币抛掷5次，50次，500次，各做10遍，用 表示事件A发生的次数， 如表1.1所示。这样的试验在历史上也有不少人做过， 其中最著名的结果见表1.2 表示A发生的频率，则得到的数据

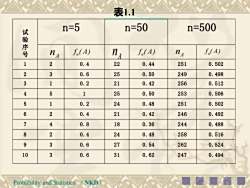
表1.1n=5n=50n=500试验序号nsf.(A)f.(A)nsf.(A)ns12220.40.442510.50223250.60.502490.49831210. 22560. 420.512541250.502530.50651240. 20. 482510.50262210. 40. 422460.49274180. 80. 362440.48882240. 40. 482580.51693270.60. 542620.524310312470. 60. 620. 494(NKD)Probability and Statistics

Probability and Statistics （NKD） A n n f ( A ) A f ( A ) n n A f ( A ) n n 试 验 序 号 n=5 n=50 n=500 1 2 0.4 22 0.44 251 0.502 2 3 0.6 25 0.50 249 0.498 3 1 0.2 21 0.42 256 0.512 4 5 1 25 0.50 253 0.506 5 1 0.2 24 0.48 251 0.502 6 2 0.4 21 0.42 246 0.492 7 4 0.8 18 0.36 244 0.488 8 2 0.4 24 0.48 258 0.516 9 3 0.6 27 0.54 262 0.524 10 3 0.6 31 0.62 247 0.494 表1.1

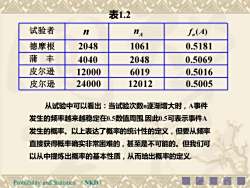
表1.2试验者NAf.(A)n德摩根204810610.5181蒲丰404020480.5069皮尔逊1200060190.5016皮尔逊24000120120.5005从试验中可以看出：当试验次数n逐渐增大时，A事件发生的频率越来越稳定在0.5数值周围.因此0.5可表示事件A发生的概率。以上表达了概率的统计性的定义，但要从频率直接获得概率确实非常困难的，甚至是不可能的。但我们可以从中提炼出概率的基本性质，从而给出概率的定义(NKDProbabilityand Statistics

Probability and Statistics （NKD） 试验者 德摩根 蒲 丰 皮尔逊 皮尔逊 n nA f (A) n 2048 1061 0.5181 4040 2048 0.5069 12000 6019 0.5016 24000 12012 0.5005 表1.2 从试验中可以看出：当试验次数n逐渐增大时，A事件 发生的频率越来越稳定在0.5数值周围.因此0.5可表示事件A 发生的概率。以上表达了概率的统计性的定义，但要从频率 直接获得概率确实非常困难的，甚至是不可能的。但我们可 以从中提炼出概率的基本性质，从而给出概率的定义

、概率的公理化定义定义2：设Q为试验E的样本空间.Q的子集A是随机事件,P(A)为实值函数，如果P(A)满足下述三条公理：1.(非负性）VA,有P(A)≥02.(规范性)对于必然事件2,有P(Q)=13.（完全可加性)对可列个两两互不相容的事件A,A,A…有: f,(ZA)=Zf.(A)l则称P(A)为随机事件A的概率,记作P(A)NKDProbabilityand Statistics

Probability and Statistics （NKD） 二、概率的公理化定义 定义2： 设Ω为试验 E 的样本空间, Ω 的子集 A 是随机事 件, P(A)为实值函数 ，如果 P(A) 满足下述三条公理： 2 3 k 1 1 1 P(A) 0 2. ( ) n i n i i i .( A, A ,A ,A ,.,A ., : f ( A ) f ( A ) ( A ) A ,   = =      = 1 非负性） 有 规范性 对于必然事件 ,有P( )=1 3.(完全可加性)对可列个两两互不相容的事件 有 则称P 为随机事件 的概率 记作P(A)

三、概率的性质1、对不可能事件①,有 P()=0证明：由于Q=Q+①+①+.+，且2,①,①...两两互不相容则 : P(2)= P(2)+ P(O)+ P()+ ..所以: P(O)+ P()+ P(O)+...=0, 又P(O)≥0则得: P(O)=02、（有限可加性）对两两互不相容的事件A,AA,有P(≥4)-P(4)证明：:乙A = A +A, + A, +...+A,+の+の+..且它们两两互不相容i=1NKDProbabilityand Statistics

Probability and Statistics （NKD） 三、概率的性质 1、对不可能事件  = , ( ) 0 有P 证明：由于 = +++ +    . . , , ,. , ，且 两两互不相容 0 0 0 : P( ) P( ) P( ) P( ) . : P( ) P( ) P( ) . , P( ) P( )  =  +  +  +  +  +  + =    = 则 所以 又 则得: 2 , , , 、（有限可加性） 对两两互不相容的事件A A A 1 2 n 有 1 1 ( ) n n i i i i P A P A = =   =       1 2 3 n A A A A . A . i n = + + + + +  +  + i=1 证明： 且它们两两互不相容

则P(ZA)= P(A)+ P( A, )+ P( A, )+.+ P( A, )+ P(O)+ P(O)+..i=1= P(A)+ P(A )+ P(A )+... + P(A )3、设A.B是任意两个事件,若ACB,则有P(B-A)= P(B)-P(A), P(B)≥ P(A)证明:：B=A+(B-A),且A与B-A互不相容则: P(B)=P(A)+P(B-A):: P(B-A)=P(B)-P(A), 同时得: P(B)≥P(A)4、对任一随机事件A,有P(A)≤1, P(A)=1-P(A)证明：：Q=A+A，则由有限可加性知P(Q)=P(A)+P(A)即P(A)+P(A)=1,则得: P(A)=1-P(A)，P(A)≤1(NKD)Probability and Statistics

Probability and Statistics （NKD） 1 2 3 1 2 3 n i n n P( A ) P( A ) P( A ) P( A ) . P( A ) P( ) P( ) . P( A ) P( A ) P( A ) . P( A ) = + + + + +  +  + = + + + +  i=1 则 3 , , , 、设A B A B 是任意两个事件 若  则有 P(B− A) = P(B)− P(A), P(B)  P(A) 证明： B A ( B A ), A B A = + − − 且 与 互不相容, : P( B ) P( A ) P( B A ) P( B A ) P( B ) P( A ), : P( B ) P( A ) = + −  − = −  则 同时得 4 , 1, ( ) 1 ( ) 、对任一随机事件A P A P A P A 有 ( )  = − 证明：  = +  = + A A P( P( A ) P( A ) ，则由有限可加性知 ） 即P( A ) P( A ) P( A ) P( A ) P( A ) . + = = −  1 1 1 ，则得：

5、（加法公式）对于任意两个事件A.B有P(AUB)= P(A)+ P(B)- P(AB)证明：由于AUB=A+（B-AB）且ABCB,由概率的基本性质2和3知：P(AUB)=P(A)+P(B-AB)= P(A)+P(B)-P(AB)加法公式的推广：1、V A,B,C三个事件：P(AUBUC)= P(A)+ P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)2、Vn个事件A,A...A,有P(UA,)=P(A)- P(AA,)+P(AA,A)-... +(-1)"-P(AA...A,i=lI<i<jSnl<i<j<k≤nNKDProbability and Statistics

Probability and Statistics （NKD） , ( ) ( ) ( ) ( ) A B P A B P A P B P AB = + − 5、（加法公式）对于任意两个事件 有 3 A B A ( B AB ), B AB ) B P AB ) = + −  − = − 证明：由于 且AB B, 由概率的基本性质2和 知： P(A B)=P(A)+P( P(A)+P( ） （ 加法公式的推广： 1、 A,B,C三个事件： P( A B C ) P( A ) P( B ) P(C ) P( AB ) P( AC ) P( BC ) P( ABC ) = + + − − − + 1 2 1 1 1 1 2 1 n n n i i j i j k i j n i i j n i j k n n A ,A .A ) P( A ) P( A A ) P( A A A ) . ( ) P( A A .A ) − =         = − + − + −    n i i=1 、 个事件 ， 有： P( A

例1：设 A、B是两个随机事件，已知：P(A)=0.6,P(B)= 0.5, P(AB) = 0.4,求P(B- A), P(A), P(AUB)与P(AB)解：由概率的基本性质：P(B- A)=P(B)-P(AB)=0.5-0.4=0.1P(A)=1- P(A) =1-0.6= 0.4P(AUB)= P(A)+P(B)-P(AB)= 0.6+0.5-0.4 = 0.7因为: AB= A-AB,且: ABC A则: P(AB)=P (A)-P (AB)=0. 6-0. 4=0. 2NKDProbabilityand Statistics

Probability and Statistics （NKD） 0.6, ( ) 0.5 , ( ) 0.4, ( ) , ( ) ( ) ( ). A B P B = = − P AB P B A P A P A B P AB 例1：设 、 是两个随机事件，已知：P(A)= 求 ， 与 解：由概率的基本性质： P( B A ) P( B ) P( AB ) . . . − = − = − = 0 5 0 4 0 1 1 1 0 6 0 4 0 6 0 5 0 4 0 7 P( A ) P( A ) . . P( A B ) P( A ) P( B ) P( AB ) . . . . AB A AB, AB A, = − = − = = + − = + − = 因为： = −  且： 则：P(AB)=P(A)-P(AB)=0.6-0.4=0.2

例2: 已知 : P(A)=P(B)=P(C)=1/4,P(AB)=0,P(AC)=P(BC)=1/6,求A,B,C中至少有一个发生的概率解: P(AUBUC)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)115116612444(注：P(ABC)=O)NKDProbabilityand Statistics

Probability and Statistics （NKD） 例2：已知：P(A)=P(B)=P(C)=1/4,P(AB)=0, P(AC)=P(BC)=1/6,求A,B,C中至少有一个发生的概率. P( A B C ) P( A ) P( B ) P(C ) P( AB ) P( AC ) P( BC ) P( ABC ) = + + − − − + 解： 1 1 1 1 1 5 4 4 4 6 6 12 = + + − − = （注：P(ABC)=0）