《概率论与数理统计》课程教学课件（PPT讲稿）第二章 随机变量及其分布 2.3 连续型随机变量的概率分布

2.3连续型随机变量的概率分布一.连续型随机变量定义：设随机变量X的分布函数F(x)，如果存在一个非负可积函数(x)，对任意实数x，有F(x) = /m f(x)dx则称这类随机变量X为连续型随机变量。称其中的(x）为X的分布密度或概率密度简称密度。称相应的分布为连续型分布

2.3 连续型随机变量的概率分布 一.连续型随机变量定义： 设随机变量X的分布函数F(x)，如果存在一个 非负可积函数f(x)，对任意实数x ，有 − = x F(x) f (x)dx 则称这类随机变量X为连续型随机变量。 称相应的分布为连续型分布。 称其中的f(x)为X的分布密度或概率密度, 简称密度

注①：连续型随机变量的分布函数必定连续：分布函数连续的随机变量未必是连续型的随机变量注②：连续型随机变量取任意一点的概率必为零注③：不可能事件的概率为0，概率为0的事件并不一定是不可能事件必然事件的概率为1，概率为1的事件不一定是必然事件

注①：连续型随机变量的分布函数必定连续；分布 函数连续的随机变量未必是连续型的随机变量； 注②：连续型随机变量取任意一点的概率必为零； 注③：不可能事件的概率为0， 概率为0的事件并不一定是不可能事件； 必然事件的概率为1， 概率为1的事件不一定是必然事件

二.连续型随机变量密度函数性质：1°密度函数f(x)在(-o0,+o)上满足f(x) ≥0, f f(x)dx =12°在f(x)的连续点处F(x)可导,且F'(x) = f(x)3°对任意的实数a,b(a<b)都有Pla≤X≤b) =Pa<X<b)=Pia≤X<b= P(a<X≤b)= f" f(x)dx

1 密度函数 f (x) 在(-∞, +∞) 上满足 ( )  0, ( ) = 1  +  − f x f x dx 2 在 f (x) 的连续点处Ｆ(x)可导, 且 3 对任意的实数a, b (a＜b)都有 F(x) = f (x)  = b a f (x)dx P{a  X  b} = P{a  X  b} = P{a  X  b} = P{a  X  b} 二.连续型随机变量密度函数性质：

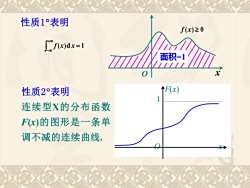
性质1°表明f(x)≥0 f(x)dx=1面积=1T/////o1XF(x)性质2°表明连续型X的分布函数F(x)的图形是一条单调不减的连续曲线

面积=1 O x 性质1表明 性质2表明 连续型X的分布函数 F(x)的图形是一条单 调不减的连续曲线. F(x) 1 O x ( )d = 1  + − f x x f (x)  0

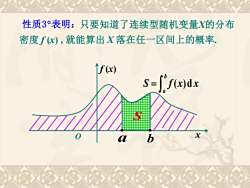
性质3°表明：只要知道了连续型随机变量X的分布密度f(x），就能算出X落在任一区间上的概率f (x)S=f(x)dx1177b

只要知道了连续型随机变量X的分布 密度 f (x) , 就能算出 X 落在任一区间上的概率. S f x x b a ( )d  = S a b x f (x) O • • 性质3表明：

例1设随机变量X具有分布密度kx,0≤x<3f(x)=32-x/2,3≤x≤4其它[0,(2) 求P(1< X ≤,(1) 确定常数k;;(3)分布函数F(x)。1解 (l)令1=f f(x)dx=['kxdx+(2-=)dx91-k+得k=426·71241(2) P(1<X≤号}=]T(2dxxdx?48216

     −     = 0, 其 它 2 / 2, 3 4 , 0 3 ( ) x x kx x f x 解   − (1) 令1 = f (x)d x 设随机变量X具有分布密度 确定常数 求 };(3)分布函数 ( )。 2 7 (1) k; (2) P{1 X  F x 例1 x x kx x )d 2 d (2 3 0 4  3 = + − 6 1 得 k = 4 1 2 9 = k + } 2 7 (2) P{1  X  48 41 =   = + − 7/ 2 3 3 1 )d 2 d (2 6 1 x x x x

0x人02x0≤x人312(3) F(x) =f(x)dx :2r+2x-33<x人44x≥4福课后：画X分布函数图形来验证F(x)的性质

−           − + −   = = x x x x x x x x F x f x d x 1 4 2 3 3 4 4 0 3 12 0 0 (3) ( ) ( ) 2 2    课后：画X分布函数图形来验证F(x)的性质

三.常用的连续型随机变量的分布均匀分布设随机变量X具有概率密度1a<x<bf(x)=3 b-a其它0,则称服从区间（a,b)上的均匀分布，记作X~U(a,b)图形：b

均匀分布 设随机变量X 具有概率密度        = − 0, 其 它 , 1 ( ) a x b f x b a 则称X服从区间(a,b)上的均匀分布, 记作 X ~ U(a,b) O x f ( x) • a • b ( ) 1 b − a 三.常用的连续型随机变量的分布 图形：

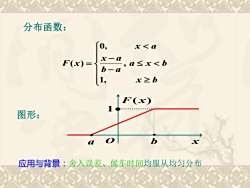
分布函数：0,x<axaF(x) =a≤x<bb-a1x≥bF(x)图形：b应用与背景：舍入误差，候车时间均服从均匀分布

          − −  = x b a x b b a x a x a F x 1, , 0, ( ) O x F(x) • a • b 1• 应用与背景：舍入误差、候车时间均服从均匀分布 分布函数： 图形：

例2:设电阻值R是个随机变量，均匀分布在900~1100欧，求R的概率密度即R落在950~1050欧的概率。解：R的密度函数为1900人r人1100f(x) =200其他0故1050P(950 人r 人1050)=dr2200J950

例2：设电阻值R是个随机变量，均匀分布 在 900~1100欧，求R的概率密度即R 落在950~1050欧的概率。 故     = 0 其他 900 1100 200 1 ( )  r  f x 解：R的密度函数为 2 1 200 1 (950 1050 ) 1050 950 = =  P  r  d r