《复变函数与积分变换》课程教学资源（教材讲义）第四章 解析函数的级数表示

第四章角解析函数的级数表示前两章我们用微分和积分的方法研究了钢析函数的性质，本章我们将用级数的方法研究解析函数的性质，首先讨论复数项级数，然后讨论复变函数项级数，量点是讨论幂级数和由正、负整次幕项组成的洛朗级数，并围绕如何将解析函数展开成幕级数或朗级数这一中心内容进行.这两类级数在解决各种实际问题中有着广泛的应用.它既是研究零点、奇点（特别是极点）的有力工具：也是微分方程中幕级数解法的理论基础.学习本章最好能结合复习《高等数学的级数部分，用对比的方式进行84.1复数项级数$4.1.1复数序列的极限设z（n=1，2，）为一复数列其中十iy，设=riyo为一确定的复数，如果任意给定ε>0，存在自然数N，使当n>Λ时，总有一之<e成立，则称复数序列收敛于复数·或称以之。为极限，记作lim =或→(n→w)如果序列（不收敛，则称（之，发散，或者说它是发散序列定理4.1设2=rn十iyo,z=十iy（n=1,2.）.则limz=2的充分必要条件是：limr,-"..limyu-y..证由不等式

第四章.80.解析备故的级数表示L4nllx2及Iva -zi.即得条件的必要性.而出不等式-≤！+-又可得条件的充分性关于两个实数序列相应项之和、差、积、商所成序列的极限的结果，不难推广到复数序列.$4.1.2复数项级数设（n一12，）为一复数序列，表达式2=++++(4. 1)称为复数项无穷级数.如果它的部分和序列Sn=21+22 +...+2#(n-1,2,3,)有极限limS.=S（有限复数），则称级数是收敛的，S称为级数的和；如果（S1没有极限，就称级数（4.1）为发散的，例4.1当|！<1时，判断级数1+++++.是否收敛？解先作部分和2+12*1S=1+++21.12112一由于|2|<1,所以lim/+1=0,因而[≥/ *+1limlim0,-Z.1于是2+,lim0.2故12+1limS. - limZ*= lim2ock-l-

+82+第四章解析函数的级教表示来，若，收敛，级数||却不一定收敛.我们把，收敛而之i不收敛的级数之，称为是条件收敛的，例4.2划别下列级数的收敛性(3)2.1i21?(2)(1)e1-4发散，所以根据定理4.2即知≥（+）发散(1)由≥解21n（2）显然11+1-1+电电46-821:11+ ij 1 ++只收敛，但是的实部与虚部（两级数）都收敛，故之i发散,因而之条件收敛级数n1含素是收效的正项级数,所以根据定理4.4 知W(3）由于1级数≥是收敛，且为绝对收敛。11484.2复变函数项级数4.2.1复变函数项级数设(f,（z))（n=1,2,)为区域D内的函数,则称2f.(x) = fi(2) + f2(2) + .. + f,(2) + ...(4. 2)

31.2复变羽数须级数83为区域D内的复变函数项级数.该级数前n项的和S() =- f() -f.(2) ++ f()称为级数的部分和。设为区城D内的一点·如果lmS（，）=S（）存在，则称级数（4.2)在处是收敛的.S（2）就是它的和，即/（）-S（）.如果级数在1)内处处收敛，这时，级数（1.2)的和是I)内的-个函数S（z）即f.(2) -S(c).警如，例4.1中的级数1十+十→十在区域|1内收1，也就是说在区域2≤1内1十十敛，且在该区域内的和函数为一"+…+"+…收敛于i下面我们主要研究经常用到的复变函数项级数的简单情形一幂级数和含有正幂项、负幂项的级数，它们与解析函数有着密切的关系，$4.2.2幂级数和实变量的幂级数样，形如C,(—20)"=C +C(-2)+C(-2,) ++C-2)"+.(4.3)的复函数项级数称为幕级数·其中（，（一0，1.2，）及均为复常数下面我们讨论幂级数的收敛集合显然，名，是级数（4.3）的收敛点.对于该幂级数在。外其它点是否收敛的问题.和实变量幂级数一样，有下述阿贝尔（Abel）定理定理4.5如果幂级数（4.3)在点2l（手2）收敏、则级数（1.3）在圆域|<一内绝对收敛证设为圆域-<一内任-点（图4.1(a))因为ZC.(2 - z0)

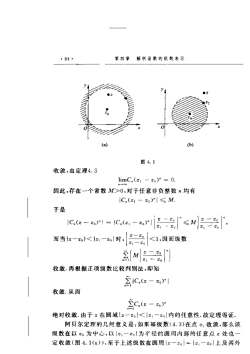
第四章解析函数的级数表示8480(a)(b)图 4. 1收敛，由定理4.3limC,(z1--2)"=0.因此，存在一个常数M0，对于任意非负整数n均有IC,(z- zo)"I≤ M.于是[C,(2—20)"!=1C(z-20)"M而当1z一21<12一01时，<1,因而级数2(M)收敛.再根据正项级数比较判别法，即知2IC,(2 - 20)1收敛.从而EC(z-2)绝对收敛，由于之在圆域（之一<|之，一名|内的任意性，故定理得证，阿贝尔定理的几何意义是：如果幂级数（4.3）在点1收敛，那么该级数在以。为中心，以&一为半径的圆周内部的任意点之处也一定收敛（图4.1（a）），至于上述级数在圆周一|=「,一|上及其外

$1.2复变函数项级数+85.部的收敛性，除点；以外，须另行判定，推论如果称级数（4、3)在点名发散，则满足i之一2。，≥1z2一。l的点，都使级数（4.3）发散证用反证法，设为满足一2-的任一点，若在处级数（4.3）收敛，则由阿贝尔定理知2C,(2z0)"收敛这与题设矛盾.因而满足一≥|一|的点均使级数（4.3）发散.证毕这个推论的儿何意义是：如果幂级数（4.3）在点22发散，那么该级数在以为中心、一。为半径的圆周外部的任意点处，必然也发散（图4.1（b)).而该级数在圆周！2一2。|=1：一2上或其内部的敛散性，则须另行讨论，对于一个形如（4.3）的幂级数.当≠。时，可能有三种情况第一种对任意的，级数C,（一）"均发散例如级数1+(）+2(z)++(）"+当之≠2。时，通项不趋于零，故发散，第二种对任意的，级数C（一）”均收敛.例如级数1 +(2-0) +(2-)2(之20)22n"21对任意固定的之，从某个n开始，以后总有于是从此以后n有，因而级数对任意的均收敛，第三种存在一点21≠z，使≥C（z一2）"收敛（此时，根据定理4.5知≥C,(z—2,)"在圆周[—2|=|2)-2|内绝对收敛）,另外

-86.第四章解析函数的级数表示又存在点z2使C,(z2—20)”发散(|z2—21>[z1—2l,由定理4.5的推论知它在圆周一一的外部发散)在这种情况下，可以证明，存在-个有限止数R，使得C,一）"在-~。|=R内绝对收敛,在圆周i2--2=R的外部发散.R称为此幂级数的收敛半径；圆周|≥一z.i=R称为收敛圆.对第一种情形，约定R一0：对第二种情形，约定R=0.并且称它们为收敛半径.现在讨论关于幂级数（4.3）的收敛半径R的具体求法.同实幂级数类似，比值法和根值法是我们熟悉的两个有效的常用方法（证明从略),L=,则级数C（—2）"的收敛半径（1）比值法：若lim1R=X（2）根值法：设lim/TCT入，则级数C,（z一）"的收敛半径R=1X当入=0时，则R=0当入8时，则R=0例4.3求级数≥，2≤，2的收敏半径、并讨论它们在收敛圆上的敛散性，解这三个级数都有lim=1，故R=1.但它们在收敛圆[|=1上的敛散性却不一样，2在|2|=1上由于lim2≠0,故在|2|1上处处发散，在|2|=1上的α=—1处收敛,z=1处发散，≤在1z{=1上处处绝对收敛,因而也是处处收敛

4.2复变函数项级数87.由此例可知，收敛圆上的情况是复杂的，只能对具体级数进行具体分析，（2一1的收敛半径例 4. 4求级数21Cn+解lim-lim"m=1,放=1.-收敛圆为|≥-1|=1.当≥=0时，原级数成为芝（1）1，为交错n级数，是收敛的；当之一2时.原级数成为一，是调和级数，是发散的。与实幂级数一样，复幕级数也能进行加、减、乘等运算，设f(2) = EC.2", 1zi<ri-g(2) -Ebhe",1z/<r2则在l|<min（rr.)内，两个幕级数可以像多项式那样进行相加、相减、相乘，所得的幂级数的和函数分别是（之）与g（）的和、差、积特别要指出的是，代换（复合）运算在把函数展开成筹级数时，有着广泛应用.通过下面的例题具体说明，把函数表成形如c（z2”的幂级数.例4.51111解 2+(2-2)21-3-22由例4.1可推知，当<1 时,有1=1+(*2)+["2) +1-2-22…+2"+.2因而有1=-（- 2) +(-2)2+22—221...+ (-1)"2(2 - 2)" +

34.3泰勒(Taylor)级数891根据例4.1.就有展开式由于在C上，而在C内，所以111(S2.）(&-z)2-N5-2-2012+-一1r(9-)1(z -20).将上式代入（4.5）式，并把它写成o-s[](z - 20)"+R(2),(4.6)2元iJ其中f(9)1R.(2) =(5- 2)0-1(2Y2元十下证limR()-0由于（z）在D内解析，从而在C上连续.因此，存在-个正常数M,在C上f()≤M,又由于12-202-20q<1,-20r于是有f(s)16IR()]≤Idz(z20)" (g - 20)0-)2元9d?Myn1SM.q"-2元r2元1-9因为limqN=0，所以limR（z）=0在C内成立.又可根据幂级数在收敛圆内可逐项积分的性质和高阶导数公式，（4.6）式可写为f"(zo)f(z)=f()+f(zn)(z-20)2)2+21fm(22(z—zn) +n!

· 90*第四章解析函数的级数表示即定理得证说明（1）从I面的证明知，C的半径可任意接近于R，所以f（z）在.处的幕级数的收敛半径至少等于从艺到D的边界上各点的最短距离.（4.4）式称为（z）在z的泰勒展开式.其右端的级数称为f（）在名的泰勒级数（2）应当指出，如果f（）在1）内有奇点.则使（z）在2u的泰勒展开式成立的R等于从到）的距。最近个奇点α之间的距离，即R-（3）f（）在处的泰勒展开式是惟一的.因为假设（）在处有另一展开式。F() =bo+ r(-z) + b(z-2)2 +.+6(2-2）"+"当=2时有6。一了（z。），然后按幂级数在收敛圆内可逐项求导的性f(m(zo)质，将上式两边求导后，令名一o得b一厂（2）同理可得b=n!(n-0,1.2,...).将定理4.6同幂级数的性质相结合，就得到个重要的结论：函数在一点解析的充分必要条件是它在这点的邻域内可以展开为幂级数这个性质从级数的角度深刻地反映了解析函数的本质，因泰勒展开式是惟一的.所以，我们可以用任何可能的方法将解析函数（）在某个解析点z的邻域内展开为泰勒级数、下面我们举例说明.例4.6将（）=e在2=0处展开为泰勒级数fn(zo)解由于e的各阶导数等于e,且e|-=1.则C,=n!()二一，故所求的展开式为n!n!=1++++++1112121!这个级数的收敛圆可以用两种方法来确定，第一，从级数的系数，按求