《复变函数与积分变换》课程教学资源(PPT课件)第二章 解析函数 2.4 第四节 平面场的复势

复变函数*第四节平面场的复势一、用复变函数表示平面向量场二、平面流速场的复势三、静电场的复势四、小结与思考U
*第四节 平面场的复势 一、用复变函数表示平面向量场 二、平面流速场的复势 三、静电场的复势 四、小结与思考
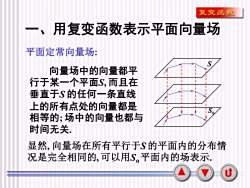
复变函数一、用复变函数表示平面向量场平面定常向量场向量场中的向量都平行于某一个平面S.而且在垂直于S的任何一条直线上的所有点处的向量都是相等的:场中的向量也都与时间无关显然,向量场在所有平行于S的平面内的分布情况是完全相同的.可以用S。平面内的场表示U
2 一、用复变函数表示平面向量场 平面定常向量场: 向量场中的向量都平 行于某一个平面S, 而且在 垂直于S 的任何一条直线 上的所有点处的向量都是 相等的; 场中的向量也都与 时间无关. S S0 显然, 向量场在所有平行于S 的平面内的分布情 况是完全相同的, 可以用So 平面内的场表示

复变函数在平面S.内取定一直角坐标系xoy向量A=Ai+A可表示为复数A=Ax+iA由于场中的点可用复数z=x+i表示所以平面向量场 A=Ax(x,J)i +A,(x,J)j可表示为复变函数 A= A(z)= Ax(x,J)+iA,(x,y)反之,已知一个复变函数w=u(x,y)+iv(x,y),也可作出对应的平面向量场 A=u(x,y)i+v(x,y)iu
3 , 在平面S0内取定一直角坐标系xoy o x y Ay A . Ax x y x y A A iA A A i A j = + = + 为复数 向量 可表示 由于场中的点可用复数 z = x + iy 表示, ( ) ( , ) ( , ). ( , ) ( , ) A A z A x y iA x y A A x y i A x y j x y x y = = + = + 示为复变函数 所以平面向量场 可表 ( , ) ( , ) . , ( , ) ( , ), A u x y i v x y j w u x y iv x y = + = + 可作出对应的平面向量场 反之 已知一个复变函数 也

复变函数例如,一个平面定常流速场(如河水的表面)= vx(x,y)i +v,(x,y)j可以用复变函数=v(z)=V(x,J)+iv,(x,y)表示平面电场强度向量为E=Ex(x,y)i+E,(x,J))可以用复变函数E=E(z)=E(x,J)+,(x,J)表示
4 例如, 一个平面定常流速场(如河水的表面) v v x y i v x y j x y = ( , ) + ( , ) 可以用复变函数v v(z) v (x, y) iv (x, y)表示, = = x + y 平面电场强度向量为 E E x y i E x y j x y = ( , ) + ( , ) . ( ) ( , ) ( , ) 表示 可以用复变函数 E E z E x y iE x y = = x + y
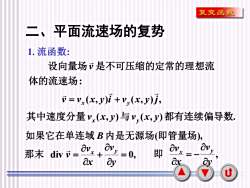
复变函数二、平面流速场的复势1.流函数:设向量场讠是不可压缩的定常的理想流体的流速场:=yx(x,y)i +v,(x,y)j其中速度分量Vx(x,J)与v,(x,J)都有连续偏导数如果它在单连域B内是无源场(即管量场)OvOvOvavx即tX那末 div =:0.二dyaxayaxU
5 二、平面流速场的复势 1. 流函数: : 体的流速场 设向量场v 是不可压缩的定常的理想流 v v (x, y)i v (x, y) j, x y = + 其中速度分量v (x, y)与v (x, y)都有连续偏导数. x y 如果它在单连域 B 内是无源场(即管量场), div = 0, + = y v x v v 那末 x y , y v x vx y = − 即

复变函数于是v,dx+v.dy为某个二元函数y(x,)的全微分,dy(x,y) =-v,dx +Vrdyayay=V-y'axay因为等值线 y(x,y)=c—流线dyVdy(x,j)=-v,dx+Vrdy= 0, 所以dxV场在等值线(x,y)=C上每一点处的向量都与等值线相切函数y(x,)称为场的流函数u
6 流线 , d d ( , ) 的全微分 于是 v x v y为某个二元函数 x y − y + x d (x, y) v dx v dy. = − y + x , . y x v y v x = = − ( , ) , 1 因为等值线 x y = c d (x, y) = −v dx + v dy = 0, y x . d d x y v v x y 所以 = , ( , ) 1 都与等值线相切 场v 在等值线 x y c 上每一点处的向量 v = 函 数 (x, y)称为场v 的流函数.

复变函数2.势函数:如果讠又是B内的无旋场(即势量场)OvyVx=0.即那么rot =0,axay于是vrdx+v,dy为某个二元函数p(x,j)的全微分, dp(x,y)=V,dx +v,dyagagrad@ =.VVaxay函数@(x,J)称为场的势函数(或位函数)等值线戋 (x,y)=c2等势线(或等位线)u
7 2. 势函数: 如果v 又是 B内的无旋场(即势量场), rot v = 0, 那么 = 0. − y v x v 即 y x , d d ( , ) 的全微分 于是 v x v y为某个二元函数 x y x + y d (x, y) v dx v dy, = x + y , . x y v y v x = = grad v. = 函 数 (x, y)称为场v 的势函数(或位函数). ( , ) 等势线(或等位线) 2 等值线 x y = c
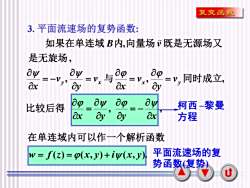
复变函数3.平面流速场的复势函数如果在单连域B内,向量场既是无源场又是无旋场,agayayap与同时成立LV三二x,4Vaxayayaxayayap0柯西-黎曼比较后得axaxOyay方程在单连域内可以作一个解析函数平面流速场的复w=f(z)=p(x,y)+iy(x,y)势函数(复势)U
8 平面流速场的复 势函数(复势) 柯西 –黎曼 方程 3. 平面流速场的复势函数: , , 是无旋场 如果在单连域 B内 向量场v 既是无源场又 , 与 y x v y v x = = − , 同时成立, x y v y v x = = , , x y y x = − = 比较后得 在单连域内可以作一个解析函数 w = f (z) = (x, y) + i(x, y)

复变函数agagagay因为 V=Vr+iv,f'(z),-1axayaxax所以流速场可以用复变函数V=f(z)表示给定一个单连域内的无源无旋平面流速场就可以构造一个解析函数一它的复势与之对应;反之,如果在某一区域(不管是否单连)内给定一个解析函数,就有以它为复势的平面流速场对应,并可以写出该场的流函数和势函数,得到流线与等势线方程,画出流线和等势线的图形,即得描绘该场的流动图象u
9 x y 因为 v = v + iv y i x + = x i x − = = f (z), 所以流速场v 可以用复变函数v = f (z)表示. 给定一个单连域内的无源无旋平面流速场, 就可以构造一个解析函数——它的复势与之对 应; 反之, 如果在某一区域(不管是否单连)内给 定一个解析函数, 就有以它为复势的平面流速 场对应, 并可以写出该场的流函数和势函数, 得 到流线与等势线方程, 画出流线和等势线的图 形, 即得描绘该场的流动图象
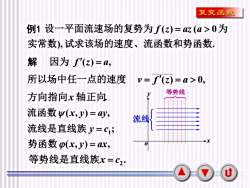
复变函数例1 设一平面流速场的复势为 f(z)=az(a>0为实常数)试求该场的速度、流函数和势函数解 因为 f(z)=a,所以场中任一点的速度v= f'(z)=a> 0,等势线y方向指向x轴正向流函数y(x,y)=ay,流线流线是直线族=C;+x势函数(x,y)=ax,0等势线是直线族x=C2u
10 例 1 ), . ( ) ( 0 实常数 试求该场的速度、流函数和势函数 设一平面流速场的复势为 f z = az a 为 解 因为 f ( z ) = a, 所以场中任一点的速度 v = f (z) = a 0, 方向指向x 轴正向. 流函数 (x, y) = ay, ;1 流线是直线族 y = c 势函数 (x, y) = ax, . 2 等势线是直线族x = c x yo 流线 等势线
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《复变函数与积分变换》课程教学资源(PPT课件)第二章 解析函数 2.3 第三节 初等函数.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第二章 解析函数 2.2 第二节 函数解析的充要条件.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第一章 复数与复变函数 1.2 第二节 复数的几何表示.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第一章 复数与复变函数 1.3 第三节 复数的乘幂与方根.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第一章 复数与复变函数 1.1 第一节 复数及其代数运算.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第一章 复数与复变函数 1.4 第四节 区域.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第一章 复数与复变函数 1.0 习题课.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第一章 复数与复变函数 1.5 第五节 复变函数.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第一章 复数与复变函数 1.6 第六节 复变函数的极限和连续性.ppt
- 《复变函数与积分变换》课程教学资源(教材讲义)第九章 拉普拉斯变换.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第八章 傅里叶变换.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第六章 共形映射.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第五章 留数及其应用.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第七章 解析函数在平面场的应用.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第一章 复数与复变函数.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第二章 解析函数.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第四章 解析函数的级数表示.doc
- 《复变函数与积分变换》课程教学资源(教材讲义)第三章 复变函数的积分.doc
- 《复变函数与积分变换》课程考试大纲 Complex Function and Integral Transformation.pdf
- 《复变函数与积分变换》课程教学大纲 Complex Function and Integral Transformation.pdf
- 《复变函数与积分变换》课程教学资源(PPT课件)第二章 解析函数 2.0 习题课.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第二章 解析函数 2.1 第一节 解析函数的概念.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第三章 复变函数的积分 3.5 第五节 柯西积分公式.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第三章 复变函数的积分 3.6 第六节 高阶导数.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第三章 复变函数的积分 3.7 第七节 解析函数与调和函数的关系.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第三章 复变函数的积分 3.0 习题课.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第三章 复变函数的积分 3.4 第四节 原函数与不定积分.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第三章 复变函数的积分 3.2 第二节 柯西-古萨基本定理.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第三章 复变函数的积分 3.3 第三节 基本定理的推广——复合闭路定理.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第三章 复变函数的积分 3.1 第一节 复变函数积分的概念.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第四章 解析函数的级数表示 4.4 第四节 洛朗级数.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第四章 解析函数的级数表示 4.0 习题课.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第四章 解析函数的级数表示 4.3 第三节 泰勒级数.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第四章 解析函数的级数表示 4.1 第一节 复数项级数.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第四章 解析函数的级数表示 4.2 第二节 幂级数.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第五章 留数及其应用 5.4 第四节 对数留数与辐角原理.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第五章 留数及其应用 5.0 习题课.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第五章 留数及其应用 5.2 第二节 留数.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第五章 留数及其应用 5.3 第三节 留数在定积分计算上的应用.ppt
- 《复变函数与积分变换》课程教学资源(PPT课件)第五章 留数及其应用 5.1 第一节 孤立奇点.ppt
