《复变函数与积分变换》课程教学资源（PPT课件）第三章 复变函数的积分 3.4 第四节 原函数与不定积分

复变函数第四节 原函数与不定积分一、主要定理和定义二、典型例题三、小结与思考u

第四节 原函数与不定积分 一、主要定理和定义 二、典型例题 三、小结与思考

复变函数主要定理和定义、E1.两个主要定理：定理一如果函数 f(z)在单连通域B内处处解析那末积分（(z)dz与连结起点及终点的路线C无关.由定理一可知：解析函数在单连通域内的积分只与起点和终点有关，（如下页图）u

2 一、主要定理和定义 定理一 . ( )d ( ) , 无 关 那末积分 与连结起点及终点的路线 如果函数 在单连通域 内处处解析 C f z z f z B C 由定理一可知: 解析函数在单连通域内的积分只与起点 和终点有关, (如下页图) 1. 两个主要定理:

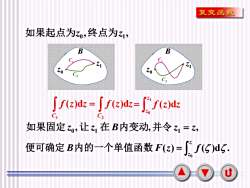
复变函数如果起点为Z,终点为zBBZ1Z1Zo10C2C2[ f(z)dz =J f(z)dz=(f(z)dz70如果固定 zo,让z 在 B内变动,并令 z= Z,便可确定 B内的一个单值函数 F(z)=(f(S)du

3 B B  0 z 1 z  0 z 1 z C1 C2 C1 C2 , , 0 1 如果起点为z 终点为z   = 1 2 ( )d ( )d C C f z z f z z  = 1 0 ( )d z z f z z , , , 0 1 1 如果固定 z 让 z 在 B内变动 并令 z = z ( ) ( )d . 0  = z z 便可确定 B内的一个单值函数 F z f  

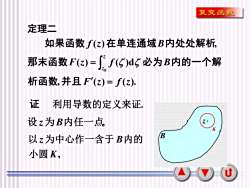
复变函数定理二如果函数 f(z)在单连通域B内处处解析那末函数F(z)=()d必为B内的一个解析函数,并且F(z)= f(z)证利用导数的定义来证。设z为B内任一点7KB以z为中心作一含于B内的小圆K,u

4 , ( ) ( ). ( ) ( )d ( ) , 0 F z f z F z f B f z B z z  = =  析函数 并 且 那末函数 必 为 内的一个解 如果函数 在单连通域 内处处解析   定理二 证 利用导数的定义来证. B 设 z为B内任一点, z , K z B 小圆 以 为中心作一含于 内的 K

复变函数取△z充分小使z +△z在K内, 由 F(z)的定义Z+AZf(S)ds -"f(S)dsF(z+ △z) - F(z) =(7由于积分与路线无关Cz+Azf(S)d的积分路线可先取Z到z,JZo2+4z（注意：这一段与f()ds的20KB路线相同）SZo然后从z沿直线到z+△z，u

5 B z K 取 z 充分小使 z + z 在 K内, z + z F(z + z) − F(z) =  − + z z z z z f f 0 0 ( )d ( )d 由于积分与路线无关, ( )d , 0 0 f z z z z z 的积分路线可先取 到 +   然后从z 沿直线到z + z,  0 z •  ) ( : ( )d 0 路线相同 注意 这一段与 的 z z f   由F(z)的定义

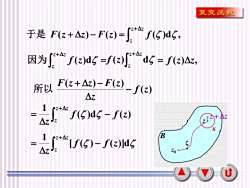
复变函数Z+4z于是 F(zz)-F()=f()ds,C+A7因为f(z)d5 =f(z)[ ds = f(z)Az,F(z+ △z)- F(z)所以-f(z)Az1Cz+zf(S)d5 - f(z)-12+4zAzJZKBzS[f() - f(z)]dsAzJzZou

6 于是 F(z + z) − F(z) = ( )d ,  z+z z f   =  z+z z 因为 f (z)d  z+z z f (z) d = f (z)z, B z K z + z  0 z •  ( ) ( ) ( ) f z z F z z F z −  +  − 所以 ( )d ( ) 1 f f z z z z z −  =  +   [ ( ) ( )]d 1 f f z z z z z −  =  +

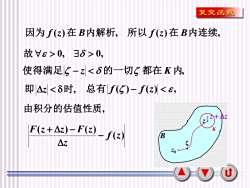
复变函数因为 f(z)在B内解析，所以 f(z)在B内连续故>0,>0,使得满足一z<的一切都在内即z<时，总有f()f(z)<,由积分的估值性质2+47F(z +△z) - F(z)K2- f(z)BAzSZou

7 B z K z + z  0 z •  因为 f (z)在 B内解析, 所以 f (z)在 B内连续, 故  0,   0, 使得满足 − z   的一切 都在 K 内, 即 z  时, 总有 f ( ) − f (z)   , 由积分的估值性质, ( ) ( ) ( ) f z z F z z F z −  +  −

复变函数F(z + △z)- F(z)Cz+Azf(z)[f(S) -f(z)]d-AzAz.Cz+Az≤f(S)-f(z)IdS≤.8.4z=8.AzJzAzF(z +△z)- F(z)于是limf(z)= 0,Azz-→0即[证毕]F'(z) = f(z)此定理与微积分学中的对变上限积分的求导定理完全类似U

8 ( ) ( ) ( ) f z z F z z F z −  +  − [ ( ) ( )]d 1 f f z z z z z −  =  + | ( ) ( )| d 1 f f z z z z z −    + . 1     =    z z ( ) 0, ( ) ( ) lim 0 − =  +  −  → f z z F z z F z z 于是即 F(z) = f (z). 此定理与微积分学中的对变上限积分的求导 定理完全类似. [证毕]

复变函数2.原函数的定义：如果函数β(z)在区域B内的导数为f(z),即β(z)= f(z),那末称(z)为f(z)在区域B内的原函数显然F(z)=(f()d是 f(z)的一个原函数原函数之间的关系：f(z)的任何两个原函数相差一个常数证设 G(z)和H(z)是 f(z)的任何两个原函数,山

9 2. 原函数的定义: . ( ) ( ), ( ) ( ) ( ) ( ), 的原函数 即 那末称 为 在区域 内 如果函数 在区域 内的导数为 z f z z f z B z B f z     = ( ) ( )d ( ) . 0 显 然F z f 是 f z 的一个原函数 z z =   原函数之间的关系: f (z)的任何两个原函数相差一个常数. 证 设G(z)和 H(z)是 f (z)的任何两个原函数

复变函数[G(z)- H(z)] = G'(z) - H(z)那末= f(z)-f(z) = 0[证毕]于是 G(z)-H(z)= c.(c为任意常数)根据以上讨论可知：如果 f(z)在区域 B内有一个原函数 F(z),那未它就有无穷多个原函数一般表达式为F(z)+c(c为任意常数)U

10 G(z) H(z) = G(z) − H(z)  那末 − = f (z) − f (z)  0 于是 G(z) − H(z) = c. (c为任意常数) 如果 f (z)在区域 B内有一个原函数 F(z), 那末它就有无穷多个原函数, 一般表达式为F(z) + c (c为任意常数). 根据以上讨论可知: [证毕]