《复变函数与积分变换》课程教学资源（PPT课件）第五章 留数及其应用 5.0 习题课

复变函数第五章留数一、重点与难点二、 内容提要三、典型例题U

复变函数一、重点与难点重点：留数的计算与留数定理难点：留数定理在定积分计算上的应用

2 一、重点与难点 重点： 难点： 留数的计算与留数定理 留数定理在定积分计算上的应用

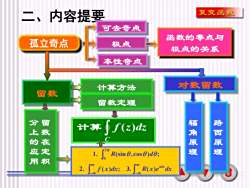
复变函数二、内容提要可去奇点函数的零点与孤立奇点极点极点的关系本性奇点对数留数计算方法留数留数定理分上的应用留数在定路西原理辐角原理f(z)dz计算R(sine,cos)de;积R(x)e*dxf(x)dx; 3

3 二、内容提要 留数 计算方法 可去奇点 孤立奇点 极点 本性奇点 函数的零点与 极点的关系 对数留数 留数定理 留 数 在 定 积 分 上 的 应 用  C 计算 f (z)dz     −  − f x dx R x e dx R d aix 2. ( ) ; 3. ( ) 1. (sin ,cos ) ; 2 0     辐 角 原 理 路 西 原 理

复变函数1.孤立奇点的概念与分类1）定义 如果函数f(z）在z不解析,但 f(z)在 Zo的某一去心邻域0<z一zo<内处处解析,则称zo 为f(z)的孤立奇点孤立奇点一奇点2）孤立奇点的分类依据()在其孤立奇点的去心邻域0<z-Zol< 内的洛朗级数的情况分为三类i）可去奇点；i)极点；ii)本性奇点U

4 1）定义 如果函数 f (z) 0 在 z 不解析, 但 f (z) 在 0 z 的某一去心邻域  −   0 0 z z 内处处解析, 则称 0 z 为 f (z) 的孤立奇点. 1. 孤立奇点的概念与分类 孤立奇点 奇点 2）孤立奇点的分类 依据 f (z) 在其孤立奇点 0 z 的去心邻域  −   0 0 z z 内的洛朗级数的情况分为三类: i) 可去奇点; ii) 极点; iii) 本性奇点

复变函数i）可去奇点定义如果洛朗级数中不含Z一Zo的负幂项，那末孤立奇点Z称为f(z）的可去奇点可去奇点的判定(a)由定义判断：如果f(z)在z。的洛朗级数无负幕项则z.为（)的可去奇点(b)判断极限lim f(z)：若极限存在且为有限值Z>z0则z为()的可去奇点U

5 定义 如果洛朗级数中不含 z − z0 的负幂项, 那末 0 孤立奇点 z 称为 f (z) 的可去奇点. i) 可去奇点

复变函数i极点定义 如果洛朗级数中只有有限多个-o的负幂项,其中关于(zzo)-的最高幂为(zzo)-m即 f(z)=+C-m(z-zo)-m +·+C-2(z-zo)-2 +C-1(z-zo)- +Co+ cCi(z - zo) +...(m ≥ 1, c-m ±0)1或写成f(z) =(z - zo)m g(2),那末孤立奇点称为函数f(z)的 m级极点u

6 ii) 极点 0 1 1 0 2 0 2 0 f (z) c (z z ) c (z z ) c (z z ) c m m = + − + + − + − + − − − − −  −  (  1,  0) −m + c1 (z − z0 ) + m c ( ) , ( ) 1 ( ) 0 g z z z f z m − = 0 定义 如果洛朗级数中只有有限多个 z − z 的 1 0 ( ) − z − z ( ) , 0 m z z − 负幂项, 其中关于 的最高幂为 − 即 那末孤立奇点 z0 称为函数 f (z) 的 m 级极点. 或写成

复变函数极点的判定方法(a)由定义判别f(z)的洛朗展开式中含有z一z.的负幂项为有限项(b)由定义的等价形式判别g(z)在点 zo的某去心邻域内f(z)E(z - Zo)m其中 g(z)在zo的邻域内解析,且 g(zo)± 0.艮 limf(z)=80 判断。(c)利用极限Z→Z0u

7 极点的判定方法 0 在点 z 的某去心邻域内 m z z g z f z ( ) ( ) ( ) − 0 = 其中 g(z) 在 z0 的邻域内解析, 且 ( ) 0. g z0  f (z) 的洛朗展开式中含有 z − z0 的负幂项为有 限项. (a) 由定义判别 (b) 由定义的等价形式判别 (c) 利用极限 =  → lim ( ) 0 f z z z 判断

复变函数i)本性奇点如果洛朗级数中含有无穷多个z一zo的负幂项那末孤立奇点Z.称为f()的本性奇点注意：在本性奇点的邻域内 lim f(z)Z→Z0不存在且不为 8.U

8 如果洛朗级数中含有无穷多个 0 z − z 那末孤立奇点 0 z 称为 f (z) 的本性奇点. 的负幂项, 注意: 在本性奇点的邻域内 lim ( ) 0 f z z→z 不存在且不为  . iii)本性奇点

复变函数3)函数的零点与极点的关系i)零点的定义 不恒等于零的解析函数 f(z)如果能表示成 f(z)=(z-z)m(z), 其中 (z)在 zo解析且 (zo）≠0,m为某一正整数，那末zo 称为f(z)的 m级零点i零点与极点的关系1如果Zo是f(z)的m级极点,那末zo就是f(z)的m级零点.反过来也成立u

9 i) 零点的定义 不恒等于零的解析函数 f (z) 如果 能表示成 ( ) ( ) ( ), 0 f z z z z m = −  (z) 0 其中 在 z ( ) 0, 解析且  z0  m为某一正整数, 那末 0 z 称为 f (z) 的 m 级零点. 3)函数的零点与极点的关系 ii)零点与极点的关系 如果 0 z 是 f (z) 的 m 级极点, 那末 0 z 就是 ( ) 1 f z 的 m 级零点. 反过来也成立

复变函数2.留数定义如果z为函数f(z)的一个孤立奇点，则沿在z的某个去心邻域0<一zol<R内包含的f(z)dz的值除任意一条简单闭曲线C的积分C以2元i后所得的数称为f(z)在z的留数记作Res[f(z),zol. (即 f(z)在z,为中心的圆环域内的洛朗级数中负幂项c-1(z一zo)-1的系数.)U

10 2. 留数 记作 Res[ ( ), ]. 0 f z z 域内的洛朗级数中负 ( ) .) 1 幂项c−1 z − z0 − 的系数 (即 f (z)在z0为中心的圆环 定义 如果 ( ) 0 z 为函数 f z 的一个孤立奇点, 则沿 在z0的某个去心邻域0  z − z0  R 内包含 0 z 的 任意一条简单闭曲线 C 的积分  C f (z)dz 的值除 2i 后所得的数称为 ( ) . 以 f z 在z0的留数