《复变函数与积分变换》课程教学资源（PPT课件）第五章 留数及其应用 5.3 第三节 留数在定积分计算上的应用

复变函数第三节留数在定积分计算上的应用一、形如Rcose,sine)de的积分二、形如R(x）dx的积分三、形如R(xleidx（a>）的积分四、小结与思考U

一、形如  的积分 2π 0 R(cos ,sin )d 二、形如  R x x 的积分 + − ( )d 三、形如  ( ) d (  0) 的积分 + − R x e x a aix 第三节 留数在定积分计算上的应用 四、小结与思考

复变函数一、形如JR(cosO,sin)de 的积分把定积分化为一个复变函数沿某条思想方法：封闭路线的积分：两个重要工作：1)积分区域的转化2）被积函数的转化u

2 一、形如  的积分 2π 0 R(cos ,sin )d 思想方法 : 封闭路线的积分 . 两个重要工作: 1) 积分区域的转化 2) 被积函数的转化 把定积分化为一个复变函数沿某条

复变函数形如 ( R(cos,sinの)dedz令=eio—d=iedde=izz-1(eio-e-iosin 0-2i2izz°+1io.AcOsO:=(e一+e三22z当 θ 历经变程[0,2元]时,z沿单位圆周z=1的正方向绕行一周U

3 形如 i 令 z = e   d d i z = ie , d d iz z  = ( ) 2 1 sin    i i e e i − = − , 2 1 2 iz z − = ( ) 2 1 cos    i i e e − = + , 2 1 2 z z + = 当  历经变程 [0,2π ] 时,  2π 0 R(cos ,sin )d z 沿单位圆周 z = 1 的正方向绕行一周

复变函数2元R(cos0,sin0)deJ0z-1dzLRt2z2记记z=1ntizl0 f(z)dz =2元Res[f(z),zk)k=1Z=包围在单位圆周z的有理函数，且在内的诸孤立奇点单位圆周上分母不为零，满足留数定理的条件：u

4 (cos ,sin )d 2π 0 R iz z iz z z z R z d 2 1 , 2 1 1 2 2  =       + − = f z z z ( )d 1  = = z的有理函数 , 且在 单位圆周上分母不 为零 , 满足留数定 理的条件 . 包围在单位圆周 内的诸孤立奇点. 2π Res ( ), . 1 = = n k k i f z z

复变函数sin?2元de例1计算积分(a>b>0J。a+bcose解令z=eio，则2°+1z2-1dz = ieiodo,cosasine一2z2zisin?0 (z -1)2dz2元de=iz2z2 +1a+ bcoso-4z[z|=1a+b2z(z - 1)2f-2iz2(b2 +2a2+b)dz.三z=1U

5 例1 计算积分 d ( 0) cos 2π sin 0 2   +  a b a b    解 , i 令 z = e 则 , 2 1 sin 2 zi z −  = , 2 1 cos 2 z z +  = d d , i z = ie iz z z z a b z z a b z d 2 1 1 4 ( 1) d cos sin 2 1 2 2 2 2π 0 2          + +  − − = +   =     = − + + − = 1 2 2 2 2 d 2 ( 2 ) ( 1) z z iz bz az b z

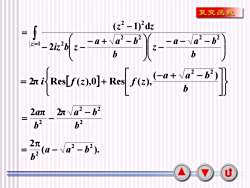
复变函数(z2-1)°dza-Va?-b?Ii-- 2i2"b z --a + a2 -67bb(-a+ Va2-b)= 2元 i Res[f(z),0]+ Res f(z),b2元 Va2 - b22a元62b22元(a- Va2 -b2)u

6 2 2 2 2 2 π 2π b a b b a − = − ( ). 2 2 2 2 a a b b − −  =  =         − − − −         − + − − − − = 1 2 2 2 2 2 2 2 2 ( 1) d z b a a b z b a a b iz b z z z               − + − = + b a a b i f z f z ( ) 2π Res ( ),0 Res ( ), 2 2

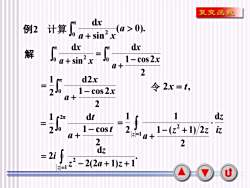
复变函数dxMT计算(a > 0).例2J0a + sin'xdxdx元元解11- cos2xJoJOa + sin'xa+2d2x令 2x=t,二一2J01 - cos2xa+21dzdt2元0二1-(z2 + 1)/2zi记22 Jo1-cost[z]=1 a+a+22dz2i0=2- 2(2a + 1)z +1z=1U

7 例2 计算 ( 0). sin π d 0 2  +  a a x x 解   − + = + π 0 π 0 2 2 1 cos 2 d sin d x a x a x x  − + = π 0 2 1 cos 2 d2 2 1 x a x 令 2x = t,  − + = 2π 0 2 1 cos d 2 1 t a t iz z z z a z d 2 1 ( 1) 2 1 2 1 1 2  − + + =  = . 2(2 1) 1 d 2 1  2 = − + + = z z a z z i

复变函数极点为：z=2a+1-/(2a+1)2-1(在单位圆内)z2=2a+1+V(2a+1)2-1 (在单位圆外)dx元所以JOa +sin'x= 2元 i. 2iRes[f(z),(2a + 1 - V(2a +1)2 -1)2元-/(2a + 1)2 -1u

8 2 1 (2 1) 1 2 极点为 : z1 = a + − a + −  + π 0 2 sin d a x x 所以 . (2 1) 1 2π 2 + − = a (在单位圆内) 2 1 (2 1) 1 2 z2 = a + + a + − (在单位圆外) 2π 2 Res[ ( ),(2 1 (2 1) 1)]. 2 = i  i f z a + − a + −

复变函数cOs20?2元例3计算 / - 1-2p00 0 p 1)的值.解由于0<p<1,1-2pcos + p2 =(1 - p)2 + 2p(1 - cos)在0≤9≤2元内不为零，故积分有意义(e2i0 + e-2i0)0) =(2 + z),由于 cs2O =二(2I = f 2'+2?1dz2izZ+Z[z|=11-2p+p2U

9 例3 d (0 1) . 1 2 cos 2π cos2 0 计算 2   的值 − + =  p p p I    解 由于0  p  1, 1 2 cos (1 ) 2 (1 cos ) 2 2 − p  + p = − p + p −  在0    2π内不为零， 故积分有意义. ( ) 2 1 cos 2 2  2   i i e e − 由于 = + ( ), 2 1 2 −2 = z + z iz z p z z p z z I z d 2 1 2 1 2 2 1 1 2 2  + + −   + = − = − 

复变函数dz1+z7=-1iz2Z+ ZCz=11-2p+p241+ z4dz = ff(z)dz.02iz(1- pz)(z - p)[z=1[z|-11被积函数的三个极点z=0,P,二pz=0,p,在圆周z=1内,且z=0为二级极点，z=p为一级极点，u

10 iz z p z z p z z I z d 2 1 2 1 2 2 1 1 2 2  + + −   + = − = −  z iz pz z p z z d 2 (1 )( ) 1 1 2 4  = − − + = , 1 0, , p 被积函数的三个极点z = p z = 0, p,在圆周z = 1内， 且z = 0为二级极点，z = p为一级极点， ( )d . 1 f z z z  = =