《复变函数与积分变换》课程教学资源（PPT课件）第六章 共形映射 6.0 习题课

复变函数第六章共形映射一、重点与难点二、 内容提要三、典型例题U

复变函数一、重点与难点重点：分式线性变换及其映射特点难点：分式线性变换与初等函数相结合，求一些简单区域之间的映射拉

2 一、重点与难点 重点： 难点： 分式线性变换及其映射特点 分式线性变换与初等函数相结合，求一 些简单区域之间的映射

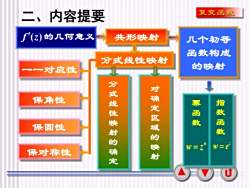
复变函数二、内容提要f(z)的几何意义共形映射几个初等函数构成分式线性映射的映射一对应性分式线性映射的确定对确定区域的映射保角性指数函数幂函数保圆性w=eW=Z保对称性

3 二、内容提要 共形映射 分式线性映射 一一对应性 保角性 保圆性 f (z) 的几何意义 几个初等 函数构成 的映射 分 式 线 性 映 射 的 确 定 对 确 定 区 域 的 映 保对称性 射 幂 函 数 指 数 函 数 z w = e n w = z

复变函数1.f(z）的几何意义设z=z(t)(α≤t≤β)表示z平面内一条有向连续曲线C,正方向为增大方向,z(t)为连续函数.如果z'(t)≠ 0,α<t< β,那么表示z(t)的向量与C相切于点z= z(to)若规定z(z)的方向(起点为z)为C上点z处切线的正向,则有(1）Argz(t)就是C上点z处的切线的正向与x轴正向之间的夹角u

4 1. 的几何意义 ( ). ( ) 0, , ( ) , , ( ) . ( )( ) 0 0 0 0 z z t z t t z t C C t z t z z t t z =      =   于点 那么表示 的向量与 相切 续曲线 正方向为 增大方向 为连续函数 如果 设 表示 平面内一条有向连     正向 则有 若规定 的方向 起点为 为 上点 处切线的 , ( ) ( ) 0 0 0 z z z C z 正向之间的夹角. f (z) (1) Argz (t 0 )就是C上点z0处的切线的正向与x轴

复变函数(2）相交于一点的两条曲线C,与C,正向之间的夹角,就是C,与C,在交点处的两条切线正响向之间的夹角设w=f(z)在区域D内解析,zo E D,且 f(zo)± 0.C：z平面内过的有向光滑曲线参数方程：z= z(t), (α≤t≤β);映射w=,f(z)将C映射成w平面内过wo= f(zo)的一条有向光滑曲线w= f[z(t)],α<z<β， 且u

5 z = z(t), (  t   ); 的一条有向光滑曲线 w = f[z(t)],  z   , 且 (2) 相交于一点的两条曲线C1与C1正向之间 之间的夹角. 的夹角,就是C1与C2在交点处的两条切线正向 ( ) , , ( ) 0. 设 w = f z 在区域D内解析 z0  D 且 f  z0  : , : C z平面内过z0的有向光滑曲线 参数方程 ( ) ( ) 0 0 映射w = f z 将C 映射成w平面内过w = f z

复变函数1）导数f(zo）≠0的幅角Arg,f(zo)是曲线C经过w=f(z)映射后在z.处的转动角2）转动角的大小与方向跟曲线C的形状与方向无关。3)保角性相交于点Z的任意两条曲线C,与C,之间的夹角在其大小和方向上都等同于经过 w= f(z)映射后跟C,与C,对应的曲线I与I,之间的夹角映射w=f(z)具有保持两曲线间夹的大小和方向不变的性质，此性质称为保角性u

6 2) 转动角的大小与方向跟曲线C的形状与方向 无关. ( ) . 1) ( ) 0 Arg ( ) 0 0 0 映射后在 处的转动角 导数 的幅角 是曲线 经过 w f z z f z f z C =    3)保角性 方向不变的性质, 此性质称为保角性. 映 射w = f (z)具有保持两曲线间夹角的大小和 夹角在其大小和方向上都等同于经过 w = f (z) . 映射后跟C1与C2对应的曲线1与2之间的夹角 相交于点z0 的任意两条曲线C1与C2之间的

复变函数4）伸缩率Ao极限f(zo)= lim△s表示C上点Z.与z间的AsZZ0弧长,Ao表示I上对应的w.与w之间的弧长)的值称为曲线C在z的伸缩率f(zo)是经过映射w=f(z)后通过点 Z的的任何曲线C在z的伸缩率,它与曲线C的形状及方向无关.所以这种映射又具有伸缩率的不变性山

7 . , ) ( ) lim ( 0 0 0 0 0 为曲线 在 的伸缩率 弧 长 表 示 上对应的 与 之间的弧长的值称 极 限 表 示 上 点 与 间 的 C z w w s C z z s f z z z       = →   4）伸缩率 f (z0 )是经过映射 w = f (z)后通过点 z0 的 的任何曲线C在 z0的伸缩率,它与曲线C的形状及 方向无关. 所以这种映射又具有伸缩率的不变性

复变函数2.共形映射（保角映射）设函数w= f(z)在区域D内解析,z为D内一点且 f(z)≠ 0,那末映射w = f(z)在zo 具有两个性质：（1）保角性；(2)伸缩率不变性定义设w=f(z)在z的邻域内是解析的在 Zo具有保角性和伸缩率不变性，那末W=f(z）在zo 是共形的，或称w=f(z)在zo 是共形映射.也称为第一类共形映射.仅保持夹角的绝对值不变而方向相反的映射，称为第二类共形映射U

8 2.共形映射（保角映射） 是共形的，或称 在 是共形映射． 具有保角性和伸缩率不变性，那末 在 定 义 设 在 的邻域内是解析的在 0 0 0 0 ( ) ( ) ( ) , z w f z z w f z w f z z z = = = 也称为第一类共形映射.仅保持夹角的绝对值不 变而方向相反的映射, 称为第二类共形映射 且 f (z)  0, 那末映射w = f (z)在z0具有两个性 质: (1) 保角性; (2) 伸缩率不变性. ( ) , , 设函数w = f z 在区域D内解析 z0为D内一点

复变函数3.分式线性映射az + b定义ad-bc± 0,a,b,c,d均为常数W=cz + d称为分式线性映射任一分式线性映射都可看成是由下列三种基本的分式映射复合而成：(1)平移映射 w= z +b;(2)旋转与相似映射w=az;(3)反演映射W=-7u

9 定 义 (ad bc 0, a,b,c,d均为常数.) cz d az b w −  + + = 称为分式线性映射. 任一分式线性映射都可看成是由下列三种基本的 分式映射复合而成: (1)平移映射 w = z + b; 3.分式线性映射 (2)旋转与相似映射w = az; . 1 (3) z 反演映射w =

复变函数分式线性映射的性质1）分式线性映射在扩充复平面上一一对应，2）分式线性映射在扩充复平面上具有保角性如果规定两条伸向无穷远的曲线在8处的夹角,等于它们在映射=二下所映成的通7过原点=0的两条象曲线的夹角，则分式线性映射是保角的U

10 分式线性映射的性质 1）分式线性映射在扩充复平面上一一对应. 2）分式线性映射在扩充复平面上具有保角性. . 0 , 1 , 性映射是保角的 过原点 的两条象曲线的夹角 则分式线 的夹角 等于它们在映射 下所映成的通 如果规定两条伸向无穷远的曲线在 处 = = =    z z