《复变函数与积分变换》课程教学资源（PPT课件）第六章 共形映射 6.1 第一节 共形映射的概念

复变函数第一节共形映射的概念一、两曲线的夹角二、解析函数导数的几何意义三、共形映射的概念四、小结与思考U

第一节 共形映射的概念 一、两曲线的夹角 二、解析函数导数的几何意义 三、共形映射的概念 四、小结与思考

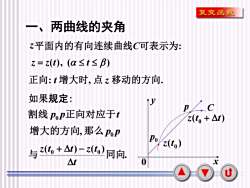
复变函数一、两曲线的夹角z平面内的有向连续曲线C可表示为：z=z(t), (α≤t≤β)正向：t增大时，点z移动的方向如果规定：tyACp割线pop正向对应于tz(t, + △t)增大的方向,那么 PoPPoz(to)与 z(tg + At) - z(tg)同向。x0△tU

2 一、两曲线的夹角 z = z(t), (  t   ) 正向: t 增大时, 点 z 移动的方向. 如果规定: 割线 p p正向对应于t 0 增大的方向,那么 p0 p . ( ) ( ) 与 0 0 同向 t z t t z t  +  − z 平面内的有向连续曲线C可表示为: y 0 x C . . 0 p p ( ) 0 z t ( ) 0 z t + t

复变函数沿C.Po时,当pC上po处切线Popz(to + △t) - z(to)2=z(to)lim方向与C一致△t△t-→01yz(to) PC如果z'(t)≠0,α<to<βz(t. + △t)那么表示z'(t.)的向量Poz(to)与C相切于点z= z(to)x0U

3 ( ) ( ) ( ) lim 0 0 0 0 z t t z t t z t t =   +  −  → 当 p , p0 时 p0 p C上 p0 处切线 ( ) 0, , 如果z  t 0    t 0   那么表示z (t 0 )的向量( ). 0 与C相切于点z = z t 方向与 C 一致. C . . 0 p p ( ) 0 z t ( ) 0 z t + t ( ) 0 z  t y 0 x 沿C

复变函数若规定(t.)的方向(起点为z)为C上点z处切线的正向，则有1.Argz(t)就是C上点z处的切线的正向与tyx轴正向之间的夹角Cz'(to)Argz(to)Zox0U

4 0 0 0 若规定z (t )的方向(起点为z )为C上点z 处切线的正向, 则有 x 轴正向之间的夹角. 1. Argz (t 0 )就是C上点z0处的切线的正向与 C . 0 z y 0 x ( ) 0 z  t Arg ( ) 0 z  t

复变函数2.相交于一点的两条曲线C,与C,正向之间的夹角,就是C,与C,在交点处的两条切线正向之间的夹角. C : z= zi(t), C2 : z= z2(t);CArgz2(to) - Argzi(to)C2zo = zi(to) = z2(to)1

5 C2 C1 2.相交于一点的两条曲线C1与C2正向之间 之间的夹角. Arg ( ) Arg ( ) 2 0 1 0 z  t − z  t . 0 z : ( ), 1 1 C z = z t : ( ); 2 2 C z = z t ( ) ( ). 0 1 0 2 0 z = z t = z t 的夹角,就是C1与C2在交点处的两条切线正向

复变函数二、解析函数导数的几何意义设w= f(z)在区域D内解析,zo D,且 f(z)≠ 0.1.Argf(zo)的几何意义C：z平面内过z的有向光滑曲线参数方程:y (z)z=z(t), (α≤t≤β);z'(to)正向：t增大的方向：c且 Zo = z(to),Zoz'(t)± 0,α<z<β.x0u

6 二、解析函数导数的几何意义 1. Argf (z0 )的几何意义 : , : C z平面内过z0的有向光滑曲线 参数方程 z = z(t), (  t   ); 正向: t 增大的方向; ( ), 0 0 且 z = z t ( ) 0, . z  t 0    z   C 0 z . y 0 x (z) 设w = f (z)在区域D内解析, ( ) 0 z  t , ( ) 0. z0  D 且 f  z0 

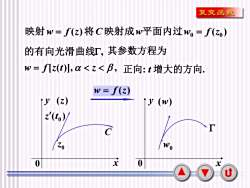
复变函数映射w= f(z)将C映射成w平面内过wo= f(zo)的有向光滑曲线，其参数方程为w=f[z(t)l,α<z<β，正向:t增大的方向,W=f(z)y (z)y (w)z'(to))TcCZowoxx00U

7 的有向光滑曲线, 其参数方程为 w = f[z(t)],  z   , 正向: t 增大的方向. ( ) ( ) 0 0 映射w = f z 将C 映射成w平面内过w = f z C 0 z . y 0 x (z) ( ) 0 z  t y 0 x (w) w0 .  w = f (z)

复变函数因为 w=f[z(t) (α≤t≤β)所以 w'(t)= w(t)l=t= F'(zo)z(to) ± 0,(即I上点wo处切线存在)Argw'(to) = Argf'(zo) + Argz(to)或Argf'(zo)= Argw(to)- Argz(to)T在w处切线的倾角C在zo处切线的倾角定义为：曲线C经w=f（z）映射后在z.的转动角U

8 因为 w = f[z(t)] (  t   ) 0 ( ) ( ) 0 t t w t w t = 所以  =   0 , ( ) 即上点w0 处切线存在 Arg ( ) Arg ( ) Arg ( ) 0 0 0 f  z = w t − z t Arg ( ) Arg ( ) Arg ( ) 0 0 0 w t = f  z + z t 或 在w0处切线的倾角C在z0处切线的倾角 定义为:曲线C经w = f (z)映射后在z0的转动角 ( ) ( ) 0 0 = f  z z t

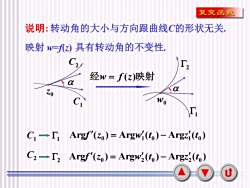
复变函数说明：转动角的大小与方向跟曲线C的形状无关映射W=(z）具有转动角的不变性CI2经w=f(z)映射αaαZoC1woFArgf'(zo) = Argw'(to) - Argz,(to)C→FC2 → I2Argf'(zo) = Argw2(to) - Argz2(to)u

9 2 1 C1 说明: 转动角的大小与方向跟曲线C的形状无关. 映射 w=f(z) 具有转动角的不变性.  . w0  经w = f (z)映射 C1 1 Arg ( ) Arg ( ) Arg ( ) 0 1 0 1 0 f  z = w t − z  t C2 2 C2 0 z . Arg ( ) Arg ( ) Arg ( ) 0 2 0 2 0 f  z = w t − z  t

复变函数则有Argw'(t.) - Argz'(to) = Argw2(to) - Argz2(to)I与I,在wo的夹角C, 与C2 在Z 的夹角结论：相交于点Z的任意两条曲线C,与C,之间的夹角在其大小和方向上都等同于经过w=f(z)映射后跟C,与C,对应的曲线I与I,之间的夹角映射w=f(z）具有保持两曲线间夹的大小和方向不变的性质，此性质称为保角性u

10 则有 Arg ( ) Arg ( ) Arg ( ) Arg ( ) 1 0 1 0 2 0 2 0 w t − z  t = w t − z  t 1 与2 在 w0的夹角 C1 与C2 在 z0的夹角 结论: 的夹角在其大小和方向上都等同于经过 w = f (z) . 映射后跟C1与C2对应的曲线1与2之间的夹角 方向不变的性质, 此性质称为保角性. 映 射w = f (z)具有保持两曲线间夹角的大小和 相交于点z0 的任意两条曲线C1与C2之间