《复变函数与积分变换》课程教学资源（PPT课件）第六章 共形映射 6.2 第二节 分式线性映射

复变函数第二节分式线性映射一、分式线性映射的概念二、几种简单的分式线性映射三、分式线性映射的性质四、小结与思考u

第二节 分式线性映射 一、分式线性映射的概念 二、几种简单的分式线性映射 三、分式线性映射的性质 四、小结与思考

复变函数一、分式线性映射的概念az + b(ad -bc ±0,a,b,C,d均为常数.)w=cz + d称为分式线性映射小知识说明：1）ad一bc≠0的限制，保证了映射的保角性dwad -bc=0,有W=常数否则，由7dz(cz + d)那末整个平面映射成w平面上的一点U

2 一、分式线性映射的概念 (ad bc 0, a,b,c,d均为常数.) cz d az b w −  + + = 称为分式线性映射. 说明: 否则, 由于 0, . d ( ) d 2 = 有  常数 + − = w cz d ad bc z w 那末整个z平面映射成 w平面上的一点. 1) ad − bc  0的限制，保证了映射的保角性. 小知识

复变函数az + b2) 由w=(ad -bc ± 0)cz + ddw+b(ad-bc±0Z:cw-a分式线性映射的逆映射.也是分式线性映射α+β三3)两分式线性映射 W(αs-β±0)ys+α'z + β(αs"-β0)仍复合为分式线性映Cyz+s"az + b射W二(ad -bc = (αs - βy)(α's"-β'r) ± 0)cz + dU

3 分式线性映射的逆映射, 也是分式线性映射. 2) 由 ( −  0) + + = ad bc cz d az b w ( −  0) − − + = ad bc cw a dw b z 3) 两分式线性映射 ( −  0) + + =        w (   −    0)  +   +  =          z z 仍复合为分式线性映 (( − = ( − )(   −  )  0)) + + = ad bc        cz d az b 射 w

复变函数4)分式线性映射α+βasα1β-W=+Y+S0+sY令51= 5 +8,52则w = A5, + B(A,B为常数)2=7S一个一般形式的分式线性映射是由下列三种特殊的简单映射复合而成：(3) w=(1) w= z+ b,(2) w = az,Zα+β对w=的研究可化为对以上映射的研究ys+s1

4 4) 分式线性映射            + +       = − + + = 1 w , 1 , 1 1 2  令 =  +   = 一个一般形式的分式线性映射是由下列三种 特殊的简单映射复合而成: (1) w = z + b, 对 的研究可化为对以上映射的研究.     + + w = ( , ) 则w = A 2 + B A B为常数 (2) w = az, . 1 (3) z w =

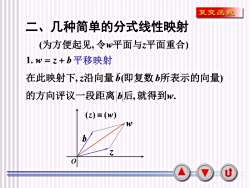
复变函数二、几种简单的分式线性映射(为方便起见，令w平面与z平面重合)1.w=z+b平移映射在此映射下，z沿向量b(即复数b所表示的向量)的方向评议一段距离b后，就得到W(z)= (w)W70u

5 二、几种简单的分式线性映射 1. w = z + b 平移映射 (为方便起见, 令w平面与z平面重合) 在此映射下, z沿向量b(即复数b所表示的向量)  的方向评议一段距离 b后,就得到w. o (z)  (w) z b w

复变函数二、几种简单的分式线性映射(为方便起见，令w平面与z平面重合)1.w=z+b平移映射在此映射下，z沿向量b(即复数b所表示的向量)的方向平移一段距离b后.就得到W(z) = (w)W110u

6 o (z)  (w) z b w 二、几种简单的分式线性映射 1. w = z + b 平移映射 (为方便起见, 令w平面与z平面重合) 在此映射下, z沿向量b(即复数b所表示的向量)  的方向平移一段距离 b后,就得到w

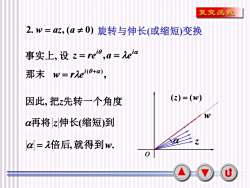
复变函数2. w=az,(a ≠ O)旋转与伸长(或缩短)变换事实上，设z=reio,a=Meiα那末 W=rei(0+α)(z) = (w)因此，把先转一个角度Wα再将z伸长(缩短)到aMα=a倍后,就得到w.0u

7 2. w = az, (a  0) 旋转与伸长(或缩短)变换 事实上, 设    i i z = re ,a = e 那末 , (  )  + = i w r e 因此, 把z先转一个角度 再将 z伸长(缩短)到  = 倍后,就得到w. w  z o (z) = (w)

复变函数3. W =反演变换Z此映射可进一步分解为W=WW=7欲由点作出点W，可考虑如下作图次序Z关于横轴对称关键：在几何上如何由z一→w,?u

8 关于横轴对称 z w 1 3. = 反演变换 此映射可进一步分解为 , 1 1 z w = w = w1 欲由点z作出点w, 可考虑如下作图次序: z → z → w1 → w 关键: 在几何上如何由z → w1 ?

复变函数对称点的定义：设C为以原点为中心.r为半径的圆周.在以圆心为起点的一条半直线上，如果有两点P与P满足关系式OP.Op'=r2,那末就称这两点为关于这圆周的对称点规定：无穷远点的对称点是圆心0.u

9 对称点的定义: 设C为以原点为中心, r为半径的圆周. 在以 圆心为起点的一条半直线上,如果有两点P与P 满足关系式 , 2 OP OP = r 那末就称这两点为关于这圆周的对称点. 规定: 无穷远点的对称点是圆心O

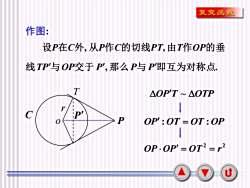
复变函数作图：设P在C外，从P作C的切线PT.由T作OP的垂线TP'与OP交于 P',那么P与 P'即互为对称点TAOP'T ～△OTPCiP'POP:OT = OT : OPO---OP:OP= OT2 = r2u

10 r C o. . P P . 设P在C外, 从P作C的切线PT, 由T作OP的垂 线TP与OP交于 P , 那么P与 P即互为对称点. OPT ~ OTP OP :OT = OT :OP 2 2 OP  OP = OT = r 作图: T