《复变函数与积分变换》课程教学资源（PPT课件）第四章 解析函数的级数表示 4.4 第四节 洛朗级数

复变函数第四节洛朗级数一、问题的引入二、洛朗级数的概念三、函数的洛朗展开式四、典型例题五、小结与思考u

第四节 洛朗级数 二、洛朗级数的概念 三、函数的洛朗展开式 一、问题的引入 五、小结与思考 四、典型例题

复变函数一、问题的引入问题:如果,f(z)在 z 不解析,是否能表示为z一zo的幂级数8c,(z- o)"1.双边幂级数n=-80n=00Zecn(z-zo)" -Ec-n(z-zo)-n +Ecn(z-zo)"n=1n=0n=-80正幂项部分负幂项部分收敛主要部分解析部分同时收敛U

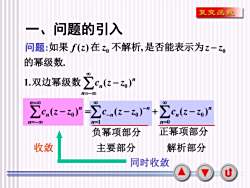
2 一、问题的引入 问题: . ( ) , 0 0 的幂级数 如果 f z 在 z 不解析 是否能表示为z − z n n n 1. c (z z )  − 0  =−  双边幂级数 负幂项部分 正幂项部分 主要部分 解析部分 同时收敛 收敛  − = = =−  n n n n c (z z ) 0 n n n n n n c (z z ) c (z z ) 0 0 0 1  − + −  = −  = −

复变函数82令=(zzo)-1Zc-n(z-zo)-n-nSCn=1n=18收敛半径Zcn(z-zo)"Rn=0SR2：两收敛域无公共部分(2)R<R2：两收敛域有公共部分R<zzo<R2u

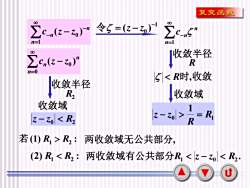
3 n n n c (z z ) 0 0  −  = n n n c z z −  =  − ( − ) 0 1 1 0 ( ) − 令 = z − z n n n c   = − 1 收敛半径   R时,收敛 0 1 1 R R z − z  = 收敛域 收敛半径 R2 0 R2 z − z  收敛域 (1) : 若 R1  R2 两收敛域无公共部分, (2) : R1  R2 两收敛域有公共部分 . 1 0 R2 R  z − z  R

复变函数2.结论：双边幂级数c,(z-zo)"的收敛区域为n=-00R2圆环域R<-Zol<R21R1常见的特殊圆环域：R2100Zo<R R<Zol000<z-zo8u

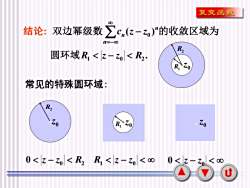
4 结论: 双边幂级数 n的收敛区域为 n n c (z z )  − 0  =−  . 1 0 R2 圆环域R  z − z  R1 R2 . 0 z 常见的特殊圆环域: R2 . 0 z 0 0 R2  z − z  R1 . 0 z R1  z − z0   0  z − z0   . 0 z

复变函数2.问题：在圆环域内解析的函数是否一定能展开成级数？在z=0及z=1都不解析例如，f(z)=z(1 - z)但在圆环域0<<1及0<z-1<1内都是解析的在圆环域0<z<1内：1f(z)=z(1 - z)1-77而1+z+z+..+z"+..z<1二1-zU

5 在圆环域 0  z  1内: 例如， 0 1 (1 ) 1 ( ) = = − = z z z z f z 在 及 都不解析, 但在圆环域 0  z  1 及 0  z − 1  1 内都是解析的. (1 ) 1 ( ) z z f z − = 而 1 , 1 1 1 2 = + + + + +  − z z z z z  n  2. 问题:在圆环域内解析的函数是否一定能展开 成级数? , 1 1 1 z − z = +

复变函数1所以 f(z)==z-1+1+z+z2+...+z"+..z(1 - z)即f(z)在 0<z<1内可以展开成级数,在圆环域0<z一1<1内，也可以展开成级数1f(z) =1-zz(1-z)z1-(1-z)[1 +(1 - z)+(1 - z)? + ...+(1 - z)" +1 - z= (1- z)-l +1+ (1-z) +(1- z)2 +(177山

6 所以 (1 ) 1 ( ) z z f z − = 1 , = z −1 + + z + z 2 ++z n + 即 f (z)在 0  z  1 内可以展开成级数. 在圆环域0  z −1  1内， 也可以展开成级数： (1 ) 1 ( ) z z f z − = (1 ) 1 (1 ) (1 ) (1 ) . = − z −1 + + − z + − z 2 + − z n−1 +  + − + − ++ − + − = n z z z z 1 (1 ) (1 ) (1 ) 1 1 2       − − − = 1 (1 ) 1 1 1 z z

复变函数二、洛朗级数的概念定理设 f(z)在圆环域R<-zol<R,内处处解析,那末f(z)在D内可展开成洛朗级数8Zf(z) =Cn(z - Zo)",n=-80f()其中2mi (c-20)m dsCn为洛朗系数(n=0,±1,..)C为圆环域内绕的任一正向简单闭曲线U

7 二、洛朗级数的概念 定理 设 f (z)在圆环域R1  z − z0  R2内处处解析， ( ) ( ) , 0 n n n f z = c z − z  =−   + − = C n n z f i c    d ( ) ( ) 2π 1 1 0 其 中 (n = 0, 1, ) C为圆环域内绕 0 的任一正向简单闭曲线. z 为洛朗系数. 那末 f (z)在 D内可展开成洛朗级数

复变函数()d5 -f()ds1证f(z)-2元iJK2- z2元iJKl- zR2对于第一个积分1K因为R,-(-zo)-(z-zo)R1.07-1 1Z-Z0<1-S5- ZoZ-Zoz - zoK5-Zo118(z- Zo)nXz -Zo22(5 - z0)n+1)- zo n=20n=0U

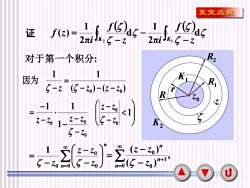
8 ( ) ( )       d 2π 1 d 2π 1 ( ) 2 1   − − − = K K z f z i f i 证 f z ( ) ( ) 1 1 0 0 z − z − z − z =  −  因为 对于第一个积分:   =       − − − = 0 0 0 0 1 n n z z z  z           − − − − −  − − = 1 1 1 1 0 0 0 0 0 z z z z z z z z   0 R z r R2 .z K1 K2 R1 . .  , ( ) ( ) 0 1 0 0   = + − − = n n n z z z 

复变函数ihad所以180f(5)Z[2m f.(-(z- Zo)nds=n+1n=080Z(z- Zo)"=6?n=0f()ds对于第二个积分：2元iJK1-z1-1[≤-α<1因为S-Zo(z)-(z)Z-Zoz - zoZ-ZoU

9 n n n c (z z ) 0 0 =  −  =    d ( ) 2π 1 2 K − z f i 所以 对于第二个积分:    d ( ) 2π 1 1 K − z f i ( ) ( ) 1 1 0 0 z − z − z − z =  −  因为          − − 1 0 0 z z  z n n K n z z z f i d ( ) ( ) ( ) 2π 1 0 0 1 0 2 −       − =    = +    0 0 0 1 1 1 z z z z z − − −  − − = 

复变函数=-(5 -20)"-1800-2( -z0)-n+1(z- zo)",(z -Zo)"n=14 ()ds则2元iJK15- zN-f(S)Z[2f.dg[(z - Zo)-n + R(z)-n+1n=1A[26-21(6)]其中dR(z)=2元iJK(z-Zo)"n=NU

10 = − −− = − 1 0 1 0 ( ) ( ) n nn z z  z ( ) , ( ) 1 0 1 1 0 n n n z z z − = − + − − = −     d ( ) 2π1 1  − − K z f i 则 其中 R N ( z ) =    d ( ) ( ) ( ) 2π1 1 01 0     − − = − K n N n n z z z f i d ( ) ( ) ( ) ( ) 2π1 0 11 1 0 1 z z R z zf i N n Nn K n − +   − = − −=  − +   