《复变函数与积分变换》课程教学资源（PPT课件）第一章 复数与复变函数 1.2 第二节 复数的几何表示

复变函数第二节复数的几何表示一、复平面二、复球面三、小结与思考u

第二节 复数的几何表示 一、复平面 二、复球面 三、小结与思考

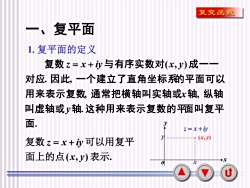
复变函数一、复平面1.复平面的定义复数z=x+i与有序实数对(x,y)成一一对应.因此，一个建立了直角坐标的平面可以用来表示复数，通常把横轴叫实轴或x轴，纵轴叫虚轴或√轴.这种用来表示复数的平面叫复平面.yz=x+iy1(x,y)复数z=x+i可以用复平面上的点(x,)表示+xX0u

2 一、复平面 1. 复平面的定义 . . , , . , ( , ) 面 叫虚轴或 轴 这种用来表示复数的平面叫复平 用来表示复数 通常把横轴叫实轴或 轴 纵 轴 对 应 因 此 一个建立了直角坐标系的平面可以 复 数 与有序实数对 成一一 y x z = x + iy x y 面上的点( , )表示. 复数 可以用复平 x y z = x + iy  (x, y) x y x y o z = x + iy

复变函数2.复数的模（或绝对值）复数z=x+i可以用复平面上的向量OP表示向量的长度称为的模或绝对值义记为z=r=/x2+y2.Pz=x+iy1显然下列各式成立+xx0[≤,x≤z,z·z==z2z≤x+yu

3 2. 复数的模(或绝对值) 向量的长度称为z的模或绝对值, 复数 z = x + iy 可以用复平面上的向量OP 表示, . 2 2 记为 z = r = x + y x y x y o z = x + iy P 显然下列各式成立 r x  z, y  z, z  x + y , . 2 2 zz = z = z

复变函数3.复数的辐角在z≠0的情况下，以正实轴为始边以表示z的向量OP为终边的角的弧度数0称为z的辐角记作 Argz=θ.说明任何一个复数z≠0有无穷多个辐角那么z的全部辐角为如果θ 是其中一个辐角Argz=,+2k元(k为任意整数)特殊地，当z=0时，z=0,辐角不确定u

4 3. 复数的辐角 Arg . , 0 , ,   =  z z OP z z 记 作 的向量 为终边的角的弧度数 称 为 的辐角 在 的情况下 以正实轴为始边 以表示 说明 任何一个复数 z  0有无穷多个辐角, , 如果1 是其中一个辐角 Arg 2 π ( ). z =  1 + k k为任意整数 特殊地, 当 z = 0时, z = 0, 那么z的全部辐角为 辐角不确定

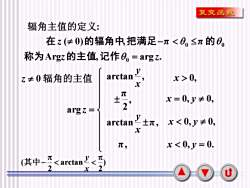
复变函数辐角主值的定义：在(0)的辐角中,把满足一元0,z≠0辐角的主值x元x = 0,y 0,2argz =3yx< 0,y± 0,±元，arctanxx<0,y= 0.元,元V元(其中.2arctan2XU

5 辐角主值的定义: Arg , arg . ( 0) , π π 0 0 0 z z z =  −      称 为 的主值 记 作 在 的辐角中 把满足 的 x  0, ) 2 arctan 2 (     − x y 其中 z  0 辐角的主值          arg z = x = 0, y  0, x  0, y  0, x  0, y = 0. arctan , x y , 2 π  arctan π, x y π

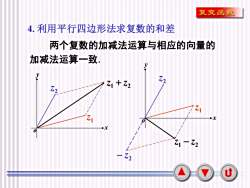
复变函数4.利用平行四边形法求复数的和差两个复数的加减法运算与相应的向量的加减法运算一致J215Z1 + Z2L7.1Z1+x+x1Z1-Z2Z.2U

6 4. 利用平行四边形法求复数的和差 x y o 1 z 2 z 1 2 z + z x y o 1 z 2 z 1 2 z − z 2 − z 两个复数的加减法运算与相应的向量的 加减法运算一致

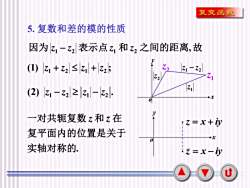
复变函数5.复数和差的模的性质因为2表示点 和 之间的距离,故2Z.2(1) 1 +z2≤+2;Z1 - Z2Z1Z2Z1(2) - 2[≥1-32+x0y一对共轭复数z和z在Iz=x+iy复平面内的位置是关于-x0实轴对称的z=x-iyU

7 5. 复数和差的模的性质 (1) ; 1 2 1 2 z + z  z + z (2) . 1 2 1 2 z − z  z − z , 因为 z1 − z2 表示点 z1 和 z2 之间的距离 故 1 z 2 z 1 2 z − z x y o 1 z 2 z . 实轴对称的 复平面内的位置是关于 一对共轭复数 z 和 z 在 x y o  z = x + iy  z = x − iy

复变函数6.复数的三角表示和指数表示x = rcoso.利用直角坐标与极坐标的关系y=rsine,复数可以表示成z=r(cos+isine)复数的三角表示式欧拉介绍再利用欧拉公式eio =cos+isinの,z=reie复数可以表示成复数的指数表示式u

8 利用直角坐标与极坐标的关系    = = sin , cos ,   y r x r 复数可以表示成 z = r(cos + isin ) 复数的三角表示式 再利用欧拉公式 cos sin ,  e i i = + 复数可以表示成 i z = re 复数的指数表示式 欧拉介绍 6.复数的三角表示和指数表示

复变函数例1将下列复数化为三角表示式与指数表示式元元(1) z = -~12 - 2i;(2) z = sin I-+icos155(cos5p + isin5)2(3) z :(cos3p-isin3p)3解(1)r=z=/12+4=4，因为z在第三象限V35-2所以θ = arctan元，一元 =arctan元=-菜-36- V12故三角表示式为 =4[cos(-~) isi(1元U

9 例1 将下列复数化为三角表示式与指数表示式: ; 5 cos 5 (1) 12 2 ; (2) sin  +  z = − − i z = i . (cos 3 sin 3 ) (cos 5 sin5 ) (3) 3 2     i i z − + = 解 (1) r = z = 12 + 4 = 4, 因为z 在第三象限, π 12 2 arctan  −      − − 所以 = = −  3 3 arctan , 6 5 = −  故三角表示式为 , 6 5 sin 6 5 4 cos              + −       z = −  i

复变函数5指数表示式为z= 4e元元显然r=z=1,(2) z = sin+icos一1553元元元元sin=coscOs一=105523元元元元sinsin=ScOS15三10523元3元”故三角表示式为+ isin=CoS10103元i指数表示式为 z=elo"U

10 指数表示式为 4 . 6 5 i z e −  = 5 cos 5 (2) sin  +  z = i 显然r = z = 1,        −  =  2 5 cos 5 sin , 10 3 cos  =        −  =  2 5 sin 5 cos , 10 3 sin  = 故三角表示式为 , 10 3 sin 10 3 cos  +  z = i 指数表示式为 . 10 3 i z e  =