《复变函数与积分变换》课程教学资源（教材讲义）第一章 复数与复变函数

目录(1)第二版前·(3)第版前言(1)第一章复数与复变函数(1)$1.1复数$1.2(5)复数的三角表示$1.3平面点集的般概念(15)$1.4(19)无穷大与复球面·81.5(22)复变函数·本章小结(27)思考题(28)习题-(28)第二童解析函数(31)$2.1解析函数的概念(31)$2.2(37)解析函数和调和函数的关系$2.3初等函数.(41)本章小结(51)思考题(52)习题二(52)第三章 复变函数的积分(55)$3.1复积分的概念(55)83.2柯西积分定理(60)$3.3柯西积分公式·(67)$3.4(72)解析函数的高阶导数本章小结(76)思考题(77)

目录2习题三(77)第四章解析函数的级数表示(79)-84.1复数项级数(79)84.2复变函数项级数..(82)$4.3泰勒级数(88)$4.4洛朗级数(94)本章小结(99)思考题·(100)习题四(100)第五章留数及其应用…(102)5.1孤立奇点...(102)$ 5. 2留数(11)5.3留数在定积分计算中的应用(120)*5.4对数留数与辐角原理.(126)本章小结(132)思考题(132)习题五(133)第六章共形映射(135)6.1共形映射的概念(135)$6.2共形映射的基本问题-(139)$6.3分式线性映射(142)$6.4几个初等丽数构成的共形映射(155)本章小结(164)习题六(165)·第七章解析函数在平面场的应用..(167)$ 7. 1复势的概念(167)$7.2复势的应用(173)$7.3用共形映射的方法研究平面场(178)本章小结(181)思考题(182)

录目3习题七(182)(183)第八章傅里叶变换8.1傅里叶变换的概念(183)88.2单位脉冲丽数（函数）(192)$8.3傅里叶变换的性质(197)本章小结(209)习题八(210)第九章拉普拉斯变换(213)$9.1拉普拉斯变换的概念(213)$ 9. 2拉氏变换的性质(217)89.3拉普拉斯逆变换(227)$9.4拉氏变换的应用及综合举例(230)本章小结(234)习题几(235)附录 1傅氏变换简表.(238)附录2拉氏变换简表(241)习题管案(246)

第一章复数与复变函数复变函数论中所研究的函数的自变量与因变量均取复数，因此，首先对于复数域以及复变量的函数要有清晰的认识，本章论述复数的基本概念、复数的四则运算、复数的三角表示、平面点集的一般概念及其复数表示，以及复变量连续函数.复数的概念、四则运算以及三角表示在现行中学数学课本中已经涉及，们可能有的读者未曾学到，因此这里仍从头开始，由于复数全体可以同平面上的点的全体作成一一对应，所以平面点集以后经常要用到.这甩仅介绍平面点集的-般概念，学习将某些简单的平面点集用含复变数的等式或不等式来表示的方法，关于复变函数，本章主要讨论连续函数的性质.许多定义与结果形式上看与高等数学中所学的颇为相似，但意义已不尽相同.希望读者在开始学习时就特别留意81.1复数$1.1.1复数的基本概念我们将形如=十i的数称为复数，其中i称为虚数单位，并规定ii.i一l.或i==i，与是任意实数.依次称为的实部（Real）与虚部（lmaginary），分别表小为Rez=a, Im z- y,例如，对复数一V2十i,有Re2=2,Im2=1.当y=0时，=+iy=十i0，我们就认为它是实数r；当r=0时，2=r十iy=0+iy，我们称它为纯虚数，并且就写作iy.例如2+i0就是实数2；0+3i是纯虚数，可以写成3；而0+0i即可看作实数0，也可

第一章复数与复变函数: 2:以着作纯虚数0i.设=，+iy与2十i是两个复数，如果=2.=则称与相等.由此得出，对于复数=十iy=0当且仅当#9=0.设=十iy是一个复数，称i为的共轭复数，记作.易知（）一之.共轭复数有很多用处，后文将逐步介绍81.1.2复数的四则运算设，=，+iy1，22一2+iy2是两个复数，定义复数的加法为：(1.1): + z = (r) + r2) +i(y + y2).复数的减法是加法的逆运算。如果存在复数使二十，则2=21—22.因此得到(1.2)2, -- z2 = (, xa) +(31 - y2).定义复数的乘法为：(1.3)zr22= (ix2 - yiy2) +i(riye + rzy).例如(2—3i)(4 + 5i)=[2·4-(—3)·5)+i[25+(-3)4]23 - 2i.由乘法定义可验证ii= (0 +1.i)(0+1.i) =--1.复数的除法是乘法的逆运算.当0时，我们说：“除以得到商”，意思就是21-22-2.从这个式子我们来求，记&一十iy.由于r, +iyi= (r + iy2)(r + iy)= (r-y2y)+i(ry+ry)根据两个复数相等的定义，得到=ty2y,yry+ry2

.4.第一章复数与复变函数(2+2)，Im2=1(2 —2).Rez=2i1例1.1设21，22是任意两个复数，求证：2Re(2122) = 2:22 + 2122.(2+2)可算得证利用公式Re222Re(2122)=2)22+(2122)=222+2232+2122学习了以上两段以后，读者可仔细体会，以加深对复数的认识，最初当给出复数概念时，我们所知道的复数是什么？复数无非是一个实数同另一个实数用""及“+”连接而写成"十i”这样一个形式的东西，“”是什么，“十”是什么意思，都未加说明.后来，介绍了复数与实数的关系，复数与纯虚数的关系，又介绍了复数加法的定义，这样，我们也就可以把r十iy看成实数z同纯虚数iy相加.其后，又定义了复数乘法，利用复数的加法与乘法，现在已可将复数&一十i真正理解为虚数i乘y，然后再加上r的结果（注意r=r+i0，y=y+i0,i=0+1i)：z=(+Oi)+(0+1i)(y+0i)-r+iy历史上，当人们第一次引进1的平方根并把它当作“数”的时候，是把它作为想像中的数，所以称为“虚数”后来就把形如，十iy的数叫做复数，意思是“复合”起来的数，81.1.3复平面一个复数十iy可唯一地对应一个有序实数对（r,y).而有序实数对与坐标yi平面上的点是一一对应的.所以，复数2xtiy全体与坐标平面上的点的全体形成一对应。现在我们直截了当地把坐标平面上0的点写成十iy（图1.1)，那么，横轴上的点就表示实数·纵轴上的点就表示纯虑图1.1数.整个坐标平面可称为复（数）平面：今

31.2复数的三角表示后我们索性将复数与复平面的点不加区分，这种点，数等同将给我们带来许多方便，在点、数等同的观点下，一个复数集合就是一个平面点集，因此，很自然地.某些特殊的平面点集就可以用复数所满足的某种关系式来表示，例如、izIm0!与z:0<Re21.0≤im2≤1分别表示上半平面与以0,1.1+i.i为顶点的正方形81.2复数的三角表示81.2.1复数的模与辐角上面说过，复数与平面上的点作成一一·对应，这是将复数实部与虚部分别看作直角坐标系下点的横坐标与纵坐标.除此以外.复数还可以同平面向量作成对应，只要将复数的实部与L虚部分别看作向量的水平分量与铅垂分量就行了.所以我们也可以把复数与平面向量等x+iy同起来.不过要注意，向量其有平移不变性即其起点可安放在任意·一点，如果把向量的起点放在（复乎面的）坐标原点，则此向量及向量的终点在上述两种对应下恰好对应同一。图 1. 2 个复数（图1.2）.如果是一个不为0的复数，我们把它所对应向量的长度叫做之的模，记作；把它所对应向量的方向角叫做2的辐角，辐角有无穷多个值，其中任意两个值相差2元的整数倍.今后，我们用记号AIg作为之的辐角的一般表示.意思是它可以不受限制地取的辐角的任意值，再用记号arg表示的所有辐角中介于一与之间（包括元）的那--个角，并把它称为≥的主辐角，即一元<arg之元（顺便指出，有的书

*6+第一章复数与复变函数把之的所有辐角中的非负最小值作为主辐角，也用记号ar之表示，这样便有0<aig2<2元）.所以Arg z = arg z+ 2k元,Y4AIg3argz(2)图1.3k是任意的整数（图1.3).当之=0时，2|=0，这时辐角没有意义.对于共轭复数，我们有1|以及arg一arg（2≠0且不为负实数，对负实数有arg=arg=).对=十iy易验证=V+因此[212 = 2 + 32 = zz.由此推出1-22对于一个不为0的复数=十iy，它的实部与虚部同它的模与辐角之间有如下的关系，一方面有=-izlcos Arg 2,y=lisin Arg 2;另一方面，反过来有12l=V+y.从而有明显的不等式Iα/≤z/, (y/≤[z],(z/≤+(y]

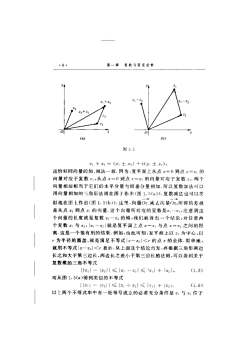
第一章-8.复数与复变函数.2Jo-(a)(b)图1. 52 + z2 =(r ±r2) +i(y ± ),这恰好同向量的加、减法一致，因为，复平面上从点一0到点=的向量对应于复数从点之=0到点2一的向量对应于复数两个向量相加相当于它们的水平分量与铅垂分量相加.所以复数加法可以用向量相加的三角形法则在图上作出（图1.5（a））.复数减法也可以类似地在图七作出（图1.5（b））.这甩向量0减去向量（)22所得的差就是从点22到点2，的向量，这个向量所对应的复数是21-2：，注意到这个向量的长度就是复数，一22的模，我们就得出一个结论：对任意两个复数与2，121—21就是复平面上点=与点=之间的距离.这是一个很有用的结果，例如，由此可知，复平面上以，为中心，以为半径的圆盘，就是满足不等式一2<r的点的全体，简单地，就用不等式|2一2<r表示.从上面这个结论出发.再根据三角形两边长之和大于第三边长，两边长之差小于第三边长的法则，可以得到关于复数模的三角不等式z/122/≤z-2/≤12+ 1z1,(1.5)而从图1.5（a）得到类似的不等式二2—22-【12-十22——2=+22](1. 6)以E两个不等式串中有一处等号成立的必要充分条件是与位于

:9S1.2复数的三角表示通过原点的同一直线上，（1.5）式与（1.6）式可以用共轭复数的性质来证明.我们以（1.6）式为例.[2+21=(2+2)(+2)212+222+222+222= 121/2 + [2,13 + 2Re(2:22),又因为[Re(2,2)1≤[z.2,1-[ [1z21=12,iz.1.所以就有[2+2≤1.1++ 21111=(.1+12),以及[,+[[22（因此（1.6）式成立，将（1.6）式中的用一替代.就得到（1.5）式，请读者留意：不等式（1.5）及（1.6）都是对复数的模而言的.复数本身不能比较大小，故不存在形如≤2的不等式81.2.3复数的三角表示设是一个不为0的复数，是的模，是的任意一个辐角，则z = r(cos 0 - i sin 0).上式右端称为复数的三角表示.反过来，对于任意的正数与实数6，r（cos+isin）·定是某个复数的一角表小.事实上，该复数一r(cos g+i sin g).一个复数的三角表示不是唯一的，因为其中的辐角有无穷多种选择.如果有两个一角表示相等：r,(cos 0.+ i sin e,)=r2(cos 0, -i sin 0,)则可推出=2.002+2k,其中，为某个整数例1.2写出复数1十1i的角表示式