《概率论与数理统计》课程教学课件（PPT讲稿）第五章 随机变量的数字特征 5.2 方差

方差5.2如果从一批灯泡抽得10个灯泡的寿命分别头700.750.750.800.800.800.850.850.900.900而从另一批灯泡抽得的10个灯泡的寿命分别为0,300,300,350,350,400,700.1900.1900.1900则不难求得这两批灯泡的平均寿命均为EX-810但第一批灯泡寿命明显稳定，因此质量好容易看到，EIX-EX)或E(X-EX)?就能度量随机变量X的稳定程度.故引入下面的定义场

如果从一批灯泡抽得10个灯泡的寿命分别为 700, 750, 750, 800, 800, 800, 850, 850, 900, 900 5.2 方差 而从另一批灯泡抽得的10个灯泡的寿命分别为 0, 300, 300, 350, 350, 400, 700, 1900, 1900, 1900 则不难求得这两批灯泡的平均寿命均为EX=810, 但第一批灯泡寿命明显稳定，因此质量好. 容易看到, E(|X-EX|)或E(X-EX) 2就能度量随机 变量X的稳定程度. 故引入下面的定义

定义1设X是一个随机变量，则称E(X一EX)(当其存在时）为X的方差，记为D(X)或DX，即DX = E(X-EX)而称√/DX为X的标准差或均方差对分布律为p的离散型随机变量，有DX = E(X - EX)° =E(x - EX)" pkk=1对密度为f(x）的连续型随机变量X,有DX = E(X - EX) = ( (x - EX)" f(x)dx

定义1 (当其存在时)为X D X DX 的方差, ( ) , 记为 或 即 对分布律为{pk }的离散型随机变量, 有 2 2 DX E X EX x EX f x x ( ) ( ) ( )d + − = − = −  2 设X E X EX 是一个随机变量,则称 ( ) − 2 DX E X EX = − ( ) 而称 DX X 为 的标准差或均方差. 对密度为f (x)的连续型随机变量X, 有 2 2 1 ( ) ( ) k k k DX E X EX x EX p + = = − = − 

方差的性质：性质1.D(C)=0.其中C为常数性质 2. DX = EX2 -(EX)性质 3. D(cX)=c2D(X).性质 4. D(X±Y)= D(X)+ D(y)±2E[X - E(X)IY - E(Y)特别，当x与Y 相互独立时，D(X±Y)=D(X)+D(y),推广: D(X+ +X, +..+ X,)-ZD(x,)+2 ZE[xX, -E(x,)[x, -E(x,)ISi<jSn特别，若X,X,,X,相互独立，则D(X, +X, +.+X,)=D(X)性质5.设X是随机变量，则DX=0的充要条件是X以概率1取常数C即 P(X =C)=1， 显然，这里C= EX.咖

方差的性质： 性质１． D C( ) = 0．其中C 为常数 性质 2． 2 2 DX EX EX = − ( ) 性质 3． D(cX ) c D(X ) 2 = ． 性质 4． D(X Y) = D(X)+ D(Y) 2EX − E(X)Y − E(Y)． 特别，当 X 与Y 相互独立时， D(X Y) = D(X )+ D(Y)． 推广： ( )  ( )   ( ) ( ) =    + + + = + − − i j n i i j j n i D X X Xn D Xi E X E X X E X 1 1 1 2  2 特别，若 X X Xn , , , 1 2  相互独立，则 ( )  ( ) = + + + = n i D X X X n D Xi 1 1 2  性质 5．设 X 是随机变量，则 DX = 0的充要条件是 X 以概率 1 取常数C ， 即 P X C  = = 1， 显然，这里C EX = ．

证明：性质1的结论显然成立：性质5的证明从略.下面证明性质2和性质4，由方差的定义及期望的性质即可推得性质 2: DX = E(X-EX) = E[X?-2X(EX)+(EX)= EX?-2(EX)(EX)+(EX)= EX?-(EX)性质 4: D(X±Y)=E[X±Y-E(X±Y)]- E[(X - EX)° +(Y - EY) ±2(X -EX)(Y - EY)= DX + DY ±2E[(X - EX)(Y - EY))特别，当X与Y相互独立时，有E[(X - EX)(Y - EY)]= E(X - EX)E(Y - EY) = 0所以D(X ±Y) = DX + DY

证明： 性质 1 的结论显然成立；性质 5 的证明从略.下面 证明性质 2 和性质 4，由方差的定义及期望的性质即可推得 性质 2： 2 2 2 DX E X EX E X X EX EX = − = − + ( ) 2 ( ) ( )     2 2 = − + EX EX EX EX 2( )( ) ( ) 2 2 = − EX EX ( ) 性质 4：   2 D X Y E X Y E X Y ( ) ( )  =  −  2 2 = − + −  − − E X EX Y EY X EX Y EY   ( ) ( ) 2( )( )   = +  − − DX DY E X EX Y EY 2 ( )( )   特别，当 X 与Y 相互独立时，有 E X EX Y EY E X EX E Y EY ( )( ) ( ) ( ) 0 − − = − − =  所以 D X Y DX DY ( )  = +

例 1求泊松分布X～P(2)的方差DX解泊松分布的分布律为?akPXkk = 0,1,2,..k!ak80(k-1) +1Z21EX2Z所以元K-K2ek!(k -1)!k=0k=181Z2k-222e(k-2)(k-1)= ae-"[ae"+e] = + a故DX = EX-(EX)=+- =

例1 e , 0,1,2, ! { = } = = − k k P X k k   所以   = − =  0 2 2 e ! k k k EX k     = − − − − + = 1 1 ( 1)! ( 1) 1 e k k k k    =  +  2 求泊松分布X～P(λ)的方差DX. 解 泊松分布的分布律为       − + − =    = −  = − − 1 1 2 2 ( 1)! 1 ( 2)! 1 e k k k k k k           =  e  e + e − = − =  +  −  =  2 2 2 2 故 DX EX (EX)

例2求正态分布X～N(u的方差DX解 正态分布V(u,c")的期望为EX=μ,密度为(x-u)212g2f(x)-8<x<+8-12元0(x-u)22g2故DX=dx2元022dt?2元

正态分布N(μ,σ 2 )的期望为EX = ,密度为 故 x σ DX x σ x μ e d 2 1 ( ) 2 2 2 ( ) 2 − + − − = −          = − t σ x μ 令 = −    +  − − x σ f x σ x μ e , 2 1 ( ) 2 2 2 ( )  例2 求正态分布 ~ ( , ) 的方差DX. 2 X N μ σ 解 2 t =  σ t t t e d 2 e 2 2 2 2 2 2 2  + − − +  − − = − +    t t t e d 2 2 2 2 2 + − − =  

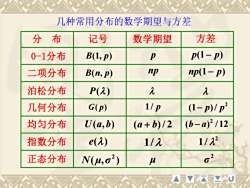
上两例表明：泊松分布P(2)的数学期望或方差完全决定了泊松分布；正态分布N(u,）的数学期望和方差完全决定了正态分布利用同样的方法亦可求得其他几种重要分布的数学期望与方差，其结果见附表1附表1列出了概率论与数理统计中几种常用的概率分布的数学期望与方差

上两例表明： 泊松分布P(λ)的数学期望或方差完全决定了泊 松分布; 正态分布N(μ,σ 2 )的数学期望和方差完全决定 了正态分布. 利用同样的方法亦可求得其他几种重要分布 的数学期望与方差, 其结果见附表1. 附表1列出了 概率论与数理统计中几种常用的概率分布的数学 期望与方差

几种常用分布的数学期望与方差方差记号分布数学期望p(1- p)B(1, P)p0-1分布npnp(1- p)二项分布B(n, p)元2P(a)泊松分布1 / pG(p)(1-p) / p2几何分布均匀分布U(a,b)(b-a)~ / 12(a + b) / 21 / 22e(a)1 / 2指数分布9正态分布N(u,o")μAKU

分 布 记号 数学期望 方差 0-1分布 二项分布 泊松分布 均匀分布 指数分布 正态分布 几何分布 B(1, p) p p(1− p) B(n, p) np np(1 − p) P( )   U(a,b) (a + b)/ 2 ( ) /12 2 b − a e() 1/  2 1 /  ( , ) 2 N μ σ μ 2 σ G( p) 1/ p 2 (1− p)/ p 几种常用分布的数学期望与方差