《复变函数与积分变换》课程教学资源（教材讲义）第八章 傅里叶变换

第八章傅里叶变换人们在处理与分析工程实际中的一些问题时，常常采取某种手段，将问题进行转换.从另个角度进行处理与分析，这就是所谓的变换为此，变换的口的无非有两个：第，，使可题的性质更清楚，更便于分析问题；第二，使问题的求解史方便，便于解决问题.但变换不同于化简它必须是可逆的，即必须有与之匹配的逆变换.由于工程实际中的问题往往是复杂的、因此变换是一种常用的手法而数学上则更是如此，直角坐标与极坐标之间是-种变换，它使我们能更灵活、更方便地处理一些问题，对数也是一种变换，它能将乘法运算化为加法运算，从而能用来求解一些复杂的代数方程.本章将要介绍的傅里叶（Fourier）1变换·则是·一种对连续时间函数的积分变换，即通过某种积分运算，把一个函数化为另一个函数，同时还具有对称形式的逆变换，它既能简化计算，如求解微分方程，化卷积为乘积等等，又具有非常特殊的物理意1义，因而在许多领域被广泛地应用.而在此基础上发展起来的离散傅里叶变换，在当今数字时代更是显得尤为重要T88.1傅里叶变换的概念1在讨论傅里叶变换之前，我们有必要先来回顾一下傅里叶级数展开，188.1.1傅里叶级数11804年，傅里叶首次提出“在有限区间上由任意图形定义的任意1函数都可以表示为单纯的正弦与余弦之和”，们并没有给出严格的证明.1829年，出法国数学家狄利克雷（Dirichlet）证明了下面的定理，为傅里叶级数奠定了理论基础1T

第八章博里叶变换184.TT定理8.1设f（t)是以T为周期的实值函数，且在[2211TT-满足狄利克雷条件（简称狄氏条件），即r（t）在门上满足22（1）连续或只有有限个第类间断点，（2）只有有限个极值点则在f(t)的连续点处有a0+f(t) = 9E(a,cas nwot + b,sin nwot),(8.1)2其中2元Wo2fr(t)cosnaotdt(n=0,l,2,...),T122b.fr(t)sin nwotdt(n -1,2,)T1在间断点t处，（8.1)式左端为号[fr(to+o)+f-(to-o)]由于正弦函数与余弦函数可以统一地由指数函数表出，因此我们可以得到另外一种更为简洁的形式.根据欧拉公式可知（其中jLV-1):1(emat+e-me)cos naot:1sin nwotnao —enen2代入（8.1)式得Zn = jbrewas + a + ibrea.aofr(t) =2222令an-jb-a+b (n = 1.2..),aoCo=Cr.222①数学中按国标规定用""表示虚数单位，这里用"j"是按照I.程中通常的习惯

$8.1傅里叶变换的彻念.183.可得ejwyfr() =(8. 2)7fr()e-'dt (n - 0, ± l, -t: 2,).(8.3)L这里系数c，既叫直接由（8.2)式以及函数族e")的正交性得到也可根据c与α，b，的关系以及α.，的计算公式得到，且c,具有唯一性，我们称（8.1）式为傅里叶级数的三角形式，而称（8.2）式为傅里叶级数的复指数形式.工程上一般采用后一种形式，傅里叶级数有非常明确的物理含义.事实上，在（8.1)式中，令A=.A=Va+,2cos 0.=半sin g,=二b(n =1,2,),AA.则(8.1)式变为ZA.(cos 9.con nwst - sin g,sin nwat)fr(t)= A+= A, + EA.cos (nout + o.).如果以f（t代表信号，则上式说明，一个周期为T的信号可以分解为简谐波之和.这些谐波的（角）频率分别为-个基频的倍数，换句话说，信号f-（t）并不含有各种频率成分，而仅由一系列具有离散频率的谐波所构成，其中A反映了频率为nw的谐波在fr（t）中所占的份额，称为振幅，，则反映了频率为n的谐波沿时间轴移动的大小，C.A,Ica!bran228B图 8. 1

第八章博里叶变换·186-称为相位，这两个指标完全刻画了信号1（1）的性态，再来看着（8.2）式，由cm与α及6的关系可得（图8.1)Ce,argc-argOVa+=Ica1lc-,1=(n = 1,2,).2因此c，作为~个复数，其模与辐角正好反映了信号（！）中频率为n的简谐波的振幅与相位，其中振幅A，被平均分配到正负频率上，而负频率的出现则完全是为了数学表示的方便，它与止频率一起构成一个简谐波，出此可见，仅由系数C就可以完全刻画信号（t）的频率特性.因此，称c为周期函数f（t)的离散频谱，c,l为离散振幅谱，argc，为离散相位谱，为了进一步明确c，与频率na，的对应关系，常常记F(nd)=cm例8.1求以T为周期的函数10,-T/2<10fr(t) =12,0<t<T/2的离散频谱和它的傅里叶级数的复指数形式解令一2元/，当n=0时，11Co=F(0) —Ifrudt =2dt=1;T示当n#0时，Ttc,= F(nw) =fr(t)e inao'dzg.,2/T-2L(e-ne"m'dt =-1)nrro,当为偶数，ie12jn元当n为奇数，元f（t)的傅里叶级数的复指数形式为2- 2ja2n130fr(t)=1+(2n— 1)元振幅谱为

88.1博里叶换的概念187[1,n=o,0,n=±2、±4..[F(no,)i2n=±1.±3.n元”相位谱为10,n二0,±2.±4，--元/2,argF(nw,)=n = 1,3,5,1元/2,n=1,-3、-5,其图形如图8.2所示。$R0)F(n0a)+ arg F(ngg)220030,RT-3003003000to00@2x2图8.288.1.2傅氏积分与傅氏变换通过前面的讨论，我们知道了一个周期函数可以展开为傅里叶级数，那么，对非周期函数是否同样适合呢?下面先直观地分析下.从物理意义上讲，傅里叶级数展开说明了周期为T的函数（t）仅包含离祭为间隔的离散频率所形成的散的频率成分，即它可由一系列以二简谐波合成（求和），因而其频谱以为间隔离散取值.当T越来越大时，取值间隔越来越小，当T趋间于无穷大时，周期函数变成了非周期函数，其频谱将在1连续取值.即·个非周期函数将包含所有的频率成分，这样离散函数的求和就变成连续函数的积分了

1第八章傅里叶变换.188-1.傅里叶积分公式我们按照上面的分析方式（即令T→+cx-），由周期函数的傅里叶级数来推导非周期函数的傅里叶积分公式，这里只是形式推导，并不是严格的证明.有关严格证明可参考数学分析方面的相关教材将非周期函数f(t)看成是由周期函数（t)当T→×时转化米的，由（8.2）式与（8.3）式有f(t)= lim f-(t)fr(r)c mad)limFCL将间篇 a记为 Aw,节点 n。 记为 α,并由 T=2=,得wuAa1limf(t) =fr(t)ewdr.elaAu-2元／e这是一个和式的极限，按照积分定义，在一定条件下，上式可写为F() = J[f(r)e-mdt Jerda.(8.4)由此得到下面的定理定理8.2（傅氏积分定理）如果f（t）在（一α0，十0）上的任一有限区间满足秋氏条件，且在（一，十）上绝对可积（即If(t) /dt<十），则（8.4)式成立.在f（)的间断点处，（8.4)式的左端应为[f(t+0)+ f(t-0)].称（8.4）式为傅里叶积分公式，简称傅氏积分。2.傅里叶变换从（8.4)式出发，令F(w) :f(t)e-mdt.(8.5)则有f(t) =I{*" F(o)erdo.(8. 6)2T

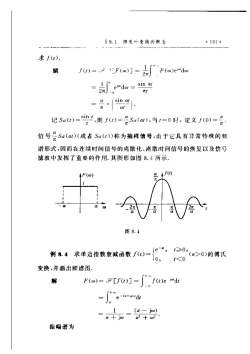
$8. 1您里听变换的概念.191.求f (t).f(1)=.21F(w)) =F(w)e"da)解sin αlemdw=2元元tin.esintaL,则f(t)二记Sa(t):Su(at)，当t=0时，定义f(0)=t7信号~Sa（αt）（或者Su（t））称为抽样信号，由于它具有非常特殊的频谱形式，因而在连续时间信号的离散化、离散时间信号的恢复以及信号滤波中发挥了重要的作用，其图形如图8.4所示，αf(t)F(0)at02元元图8.4t0例8.4求单边指数衰减函数f（）（α>0）的傅氏t<o10.变换，并画出频谱图解f(t)e mdtF(w)= Frf() =a+jadt(α - jo)1+jwa2+振幅谱为

:193:88.2单位脉冲函数（函数）x, x=0,(8. 8)p(r) = limp(r) =0,r0.显然，仅用（8.8）式这种“常规”的函数表述方式，并不能反映出质点本身的质量，必须附加一个条件p(）d=m，为此我们需要引人一个新的函数，即所谓的单位脉冲函数，又称为狄拉克函数或者函数，38.2.1单位脉冲函数的概念及其性质依照上面的例子，我们可以简单地定义单位脉冲函数（t）是满足下面两个条件的函数：(1）当t#0时，8（t）=0;8(t)dt= 1.(2)这是由狄拉克给出一种直观的定义方式，按照此定义，则例8.5中的质点的密度函数为o(r）=mo（）这里需要指出的是，上述定义方式在理$5e(0)论上是不严格的，它只是对函数的某种描述，事实上，函数并不是经典意义上的函数，而是一个广义函数，因此，关于函数的严格定义可参阅有关广义函数方面的书籍另外，函数在现实生活中也是不存在的，它是数学抽象的结果.有时入们将函数直观图8.6的理解为（t）=limo.（t），其中（t)是宽度为e高度为1/e的矩形脉冲函数（图8.6）下面我们不加证明地直接给出函数的几个基本性质，性质8.1设f(t）是定义在实数域R上的有界函数，且在1=0处连续，则?(t)f(t)dt=f(o),(8.9)一般地，若f（t）在t一点连续，则

第八章傅里叶变换,194.s( -tn)f(t)dt =f(t)(8.10)此性质称为筛选性质.其中（8.9)式给出了函数与其它函数的运算关系，它也常常被人们用来定义函数，即采用检验的方式米考察菜个函数是否为函数性质8.28函数为偶函数，即（)一8（-t)性质8.3设u（t）为单位阶跃函数，即I1.t>o.u(t)=lo.10IF(o)A解函数F(u)r((一）(w十））在与一。的冲激强度分别为元Ont和一元，其图形如图8.9所示.本例显示，利用单位脉冲函数可以将离散值以连续形式表达，从而可以统一地进行处理图 8. 9

8.2单位脉冲函数（8函数）·195.88.2.2函数的傅氏变换根据函数的定义，我们可以容易地得出函数的傅氏变换为d()edt=e-mF(w) =Sr[o(t)]-即单位脉冲函数包含各种频率分量且它们具有相等的幅度，称此为均匀频谱或白色频谱.由此我们得出，（t）与1构成傅氏变换对，按逆变换公式有1"-"[1] =1"edw = 8(t).(8.11)2元这是个关于函数的重要公式。需要注意的是，这里（）的傅氏变换仍采用傅氏变换的古典定义，但此时的广义积分是根据。函数的定义和运算性质直接给出的，而不是普通意义下的积分值，故称（t）的傅氏变换是一种广义的傅氏变换.运用这概念，我们可以对-一些常用的函数，如常数、单位阶跃函数以及正、余弦函数进行傅氏变换，尽管它们并不满足绝对可积条件.下面通过几个例子给予说明，例8.7分别求函数f（t)=1与f（t)=c的傅氏变换解由傅氏变换的定义以及（8.11)式有F.(w)=g[f()T= e-rdterdr 2元0(0),F2()= [f,(t)] - ee-mdeeg-adt - 2元o(w - w)- 2元8( - w)1+(w)例8.8试证单位阶跃函数u（t）的傅氏变换为J&