《概率论与数理统计》课程教学课件（PPT讲稿）第三章 随机向量及其分布 3.4 随机变量的独立性

3.4 随机变量的独立性利用两个事件相互独立的概念，我们自然引入两个随机变量相互独立的定义：定义1设X,Y是两个随机变量，如果对任意二实数集S,T由(XES)与YeT}构成的可能事件相互独立，则称这两个随机变量是相互独立的，简称是独立的设F(xy)及Fx(x),F)分别是随机变量X与Y的联合分布函数和边缘分布函数.则不难证明，关于两个随机变量相互独立有如下两个等价定理

定义1 设X,Y是两个随机变量, 如果对任意二 实数集S,T, 由 与 构成的可能事件相互 独立, 则称这两个随机变量是相互独立的, 简称是 独立的. 3.4 随机变量的独立性 利用两个事件相互独立的概念, 我们自然引入 两个随机变量相互独立的定义 ： 设F(x,y)及FX(x),FY (y)分别是随机变量X与Y 的联合分布函数和边缘分布函数.则不难证明,关 于两个随机变量相互独立有如下两个等价定理. { } X S  { } Y T 

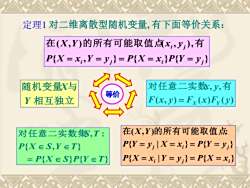
定理1对二维离散型随机变量，有下面等价关系：在(X,Y)的所有可能取值点x,,J,),有P[X =X,Y = y,}= P(X = x,}P[Y = y,}对任意二实数，y有随机变量X与等价F(x,y)=Fx(x)F(y)Y相互独立在X,Y）的所有可能取值点对任意二实数集S，T：P(Y =y; IX =x,}= P(Y = J,)PXES,YET!P(X=X,IY=y,=P(X=X,)=PXESPYE二

定理1 对二维离散型随机变量, 有下面等价关系： { | } { } { | } { } ( , ) : i j i j i j P X x Y y P X x P Y y X x P Y y X Y = = = = = = = = 在 的所有可能取值点 { , } { } { } ( , ) ( , ), i j i j i j P X x Y y P X x P Y y X Y x y = = = = = 在 的所有可能取值点 有 { } { } { , } , : P X S P Y T P X S Y T S T =     对任意二实数集 ( , ) ( ) ( ) , , F x y F x F y x y = X Y 对任意二实数 有 相互独立 随机变量 与 Y X 等价

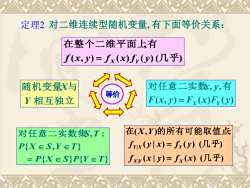
定理2对二维连续型随机变量，有下面等价关系：在整个二维平面上有f(x,y)=fx(x)f(y)(几乎)对任意二实数，y有随机变量与等价F(x,y)=Fx(x)F(y)Y相互独立在（X，Y）的所有可能取值点对任意二实数集S，T：fyx(yx)=f(y)(几乎）PXES,YET!fxr(xly)=fx(x)(几乎）=PXESPYEET

定理2 对二维连续型随机变量, 有下面等价关系： ( | ) ( ) ( ) ( | ) ( ) ( ) ( , ) : | | 几 乎 几 乎 在 的所有可能取值点 f x y f x f y x f y X Y X Y X Y X Y = = ( , ) ( ) ( ) ( ) , 几 乎 在整个二维平面上有 f x y f x f y = X Y { } { } { , } , : P X S P Y T P X S Y T S T =     对任意二实数集 ( , ) ( ) ( ) , , F x y F x F y x y = X Y 对任意二实数 有 相互独立 随机变量 与 Y X 等价

例1在3.1节例1中定义的X与Y是否相互独立？解在3.1节和3.2节已求得Y2314Pi.X001/ 40101/8021/81741/121/121/1231/401/161/161/41/161/1641332571P.j484848487由于 P(X =2)P(Y =3} =P(X = 2,Y = 3} = 0448所以，X与Y不是相互独立的

解 例1 在3.1节例1中定义的X与Y是否相互独立？ 在3.1节和3.2节已求得 P{X = 2,Y = 3} = 0 48 7 4 1 由于 P{X = 2}P{Y = 3} =  所以, X与Y 不是相互独立的.  j 1 p• 48 25 48 13 48 7 48 3 pi • 1/ 4 1/ 4 1/ 4 1/ 4 X Y 1/ 4 1/ 8 1/12 1/16 0 1/ 8 1/12 1/16 0 1/12 1/16 0 0 1/16 1 2 3 4 1 2 3 4 0 0

例2在3.1节例2中定义的X与Y是否相互独立？[2e-(2x+y), x >0,y>0解由3.1节知f(x,y)=其它[0,2e-2xe-", y>0,x>0,1 fx(x)由3.2节知f(y)=0,x≤0,0,y≤0由于对任意的(x,y)(x>0,y>0),都有fx(x)fr(y)=2e-2*e-"= f(x, J)而在其它点，都有fx(x)f,(y)= 0. 0= f(x,y)所以，X与Y是相互独立的

解 例2 由3.1节知      = − + 0, 其它 2e , 0, 0 ( , ) (2 ) x y f x y x y      = − 0, 0, 2e , 0, ( ) 2 x x f x x X      = − 0, 0 e , 0 ( ) y y f y y 由3.2节知 Y 在3.1节例2中定义的X与Y是否相互独立？ 由于对任意的(x, y) (x>0, y>0), 都有 所以, X与Y 是相互独立的. f X (x) f Y ( y) = − x − y 2e e 2 = f (x, y) 而在其它点, 都有 f X (x) f Y ( y) = 00= f (x, y)

例3讨论3.2节例3中定义的X与Y的独立性解由3.2节原题知(x-u)(x-u)(y-μ,)(y-u,)2pexp2(1-p2)a20102f(x,J)=2元,2/1-p2由3.2节知(x-u)2(y-u2)22210fx(x)fr(y) :12元012元02[a -]]22a.当且仅当=0f(x,y)2元002所以,X与Y是相互独立的充要条件是 β = 0

例3 2 1 2 2 2 2 2 1 2 1 2 2 1 2 1 2 2 1 ( )( ) ( ) 2 ( ) 2(1 ) 1 exp ( , ) σ σ ρ σ y μ σ σ x μ y μ ρ σ x μ ρ f x y −             − + − − − − − − =  讨论3.2节例3中定义的X与Y的独立性. f X (x) f Y ( y) = 2 1 2 1 2 ( ) 1 e 2 1 σ x μ σ − −  由3.2节知 解 2 2 2 2 2 ( ) 2 e 2 1 σ y μ σ − −   1 2 2 2 2 2 2 1 2 1 2 ( ) ( ) 2 1 exp σ σ σ y μ σ x μ              − + − − = f ( x, y) 当且仅当 = 0 由3.2节原题知 所以, X与Y 是相互独立的充要条件是  = 0

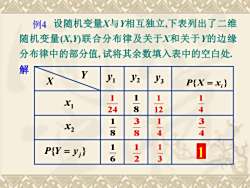
设随机变量X与Y相互独立，下表列出了二维例4随机变量X.Y联合分布律及关于X和关于Y的边缘分布律中的部分值，试将其余数填入表中的空白处解YJ1Y2y3XP(X = x,1Xi184122431831X244811P(Y = y;)236

解 设随机变量X与Y相互独立,下表列出了二维 随机变量(X,Y)联合分布律及关于X和关于Y的边缘 分布律中的部分值, 试将其余数填入表中的空白处. 例4 { } P X = xi { }j P Y = y 8 1 1 x 2 x 1 y 2 y 3 y 8 1 6 1 4 3 X Y 24 1 4 1 2 1 8 3 12 1 3 1 4 1 1