《概率论与数理统计》课程教学课件（PPT讲稿）第一章 随机事件及其概率 1.3 古典概型与几何概型

1.3古典概型与儿何概型一.古典概型古典概型满足的条件：1、样本空间包含有限个样本点2、每个样本点发生的概率是等可能的古典概型随机事件概率的计算公式定理1：设试验E为古典概型，n是其样本空间?包含的样本点数，A是E的包含k个样本点的随机事件，则事件A的概率为kA中样本点的个数P(A)=:2中样本点的个数n称此公式为古典概型的概率计算公式（或定义NKD)Probabilityand Statistics

Probability and Statistics （NKD） 一 .古典概型 古典概型满足的条件： 1、样本空间包含有限个样本点 2、 每个样本点发生的概率是等可能的. 古典概型随机事件概率的计算公式 定理1：设试验E为古典概型，n是其样本空间Ω包含的样本点 数，A是E的包含k个样本点的随机事件, 则事件A的概率为 ( ) k A P A n Ω = = 中样本点的个数 中样本点的个数 称此公式为古典概型的概率计算公式(或定义) 1.3 古典概型与几何概型

古典概型举例例1：上抛两枚硬币，出现一正一反的概率为多少解：样本空间Q=HH,HT,TH,TT其中：H表示出现正面，T表示出现反面.A表示“出现一正一反”事件，则A={HT,TH?21由于是古典概型，所以：P(A)=4-2注意：1、本题中如果样本空间认为Q={HH,TH,TT则它不是古典概型2、在求样本空间样本点的个数n及事件包含的样本点的个数k时，常常用到排列与组合的基本知识NKDProbabilityand Statistics

Probability and Statistics （NKD） 古典概型举例 例1：上抛两枚硬币，出现一正一反的概率为多少.  = { HH ,HT ,TH ,TT } A { HT ,TH } = 2 1 4 2 P( A ) = = 解：样本空间 其中：H表示出现正面，T表示出现反面.A表示 “出现一正一反”事件，则 由于是古典概型，所以： 注意：1、本题中如果样本空间认为  = { HH ,TH ,TT } 则它不是古典概型. 2、在求样本空间样本点的个数n及事件包含的样 本点的个数 k时，常常用到排列与组合的基本知识

例2：袋内有三个白球与两个黑球，从其中任取两只，求取出的两个球是白球的概率解：样本空间Q所含样本点数共C2=10个且是古典概型（等可能的），而取到两个白球的样本点的个数是C2个，则取出两个球是白球的概率：230.3p210例3：（抽球问题）袋内有a个白球与b个黑球，每次从袋中任取一个球，取出的球不再放回，接连取k(k≤α+b）个球，求第k次取出的是白球的概率NKDProbabilityand Statistics

Probability and Statistics （NKD） 例2：袋内有三个白球与两个黑球，从其中任取两只， 求取出的两个球是白球的概率.  2 5 C =10个， 2 C3 2 3 2 5 3 0 3 10 C p . C = = = 解：样本空间 所含样本点数共 且是古典概型（等可能的），而取到两个白球的样本 点的个数是 个，则取出两个球是白球的概率： 例3：（抽球问题）袋内有a个白球与b个黑球，每次 从袋中任取一个球，取出的球不再放回，接连取 k( k a b )  + 个球，求第k次取出的是白球的概率

解：由于考虑到取球的顺序，这相当于从a+b个球中任取k个球作排列，每一种取法是一基本事件，其基本事件的总和为 Pk，=（α+b）（a+b-1)：.（a+b-k+1)而第k次取得的白球可以是a个白球中的任意一个其余k-1个球是从a+b-1个球中顺次任意取出，一共有 apk-apk-aa+b-因此所求概率为ppha+ba+b可见：取得白球的概率与先后次序k无关在上例中如果是改为放回取球，结果又怎样？NKDProbability and Statistics

Probability and Statistics （NKD） 解：由于考虑到取球的顺序，这相当于从a+b个球 中任取k个球作排列，每一种取法是一基本事件， 其基本事件的总和为 k P ( a b a b+ = + ）(a+b-1).(a+b-k+1) 而第k次取得的白球可以是a个白球中的任意一个， 其余k-1个球是从a+b-1个球中顺次任意取出，一 共有 1 1 k a b aP − + − 因此所求概率为 1 P 1 P k a b k a b a a p a b − + − + = = + 可见:取得白球的概率与先后次序k无关. 在上例中如果是改为放回取球，结果又怎样?

例4：（随机取数问题）从1.210共10个数字中任取7个（可以重复），求下列各事件的概率：A：取出的7个数字全不相同：B：取出的7个数字中不含1与10C：取出的7个数字中恰好出现两次10解：从10个数字中取出7个数的每一种取法构成一基本事件.根据乘法公式：共有107种取法（与顺序有关）.则：Po870.2097P(A=0.0605,P(B107107C2.95=0.1240P(C)107（NKD)Probability and Statistics

Probability and Statistics （NKD） 例4：（随机取数问题）从1,2,···,10共10个数字中任取7个 （可以重复），求下列各事件的概率： A：取出的7个数字全不相同； B：取出的7个数字中不含1与10； C：取出的7个数字中恰好出现两次10. 解：从10个数字中取出7个数的每一种取法构成 一基本事件.根据乘法公式：共有107种取法 （与顺序有关）.则： 7 7 10 7 7 2 5 7 7 8 0 0605 0 2097 10 10 9 0 1240 10 P P( A ) . P( B ) . C P(C ) . = = = =  = =

例5：（生日问题）n个球,N个盒子(n<M），每个球等可能的被放入N个盒中，试求：（1）：指定的n个盒子中各有一球的概率（2）：恰好有n个盒子中各有一球的概率.n!n(n -1)...2.1解：(1) PNnNnPNN!.n!CN(2)P2NnNnN"(N-n)!注：“n个人生日全不相同”的概率应为：PnC36s n!365365n365n(NKD)Probability and Statistics

Probability and Statistics （NKD） 例5：（生日问题）n个球,N个盒子(n≤N) ，每个球等可能的 被放入N个盒中,试求： （1）：指定的n个盒子中各有一球的概率 ； （2）：恰好有n个盒子中各有一球的概率 。 1. p 2 p 解 ： 1 ( 1) 2 1 ! n n n n n P N N −  （1） = = ； 2 n n N N n n n C n! P N ! p N N N ( N n )!  = = = − （2） 注： “ n个人生日全不相同”的概率应为 ： 365 365 365 365 n n n n C n! P  =

解释：把n个人看成n个球（它们的生日还未知道）365天看成365个盒子，当他们的生日已知时，就看成n个人落在365个盒子中例如：n=50，p=0.0349,其相反事件"50个人中生日至少有两个人生日相同”的概率为0.9651，当n=60时概率为：0.9922NKDProbabilityand Statistics

Probability and Statistics （NKD） 解释：把n个人看成n个球（它们的生日还未知道）， 365天看成365个盒子，当他们的生日已知时，就看 成n个人落在365个盒子中. 例如：n=50，p=0.0349,其相反事件“50个人中生日 至少有两个人生日相同”的概率为0.9651，当n=60时， 概率为：0.9922

例6.任取一个两位数，求这个数能被2或3整除的概率解：设A：“取出的两位数能被2整除B：“取出的两位数能被3整除则AB表示取出的两位数能被2*3=6整除，两位数共有90个，能被2整除的有45个，能被3整除的有30个能被6整除的有15个，故由加法公式P(AUB)= P(A)+P(B)-P(AB)21545303909090NKDProbability and Statistics

Probability and Statistics （NKD） 解： 设A:“取出的两位数能被2整除” B:“取出的两位数能被3整除” 则AB 表示取出的两位数能被2*3=6整除， 两位数共有90个，能被2整除的有45个，能被3整除的有30个， 能被6整除的有15个，故由加法公式 45 30 15 2 90 90 90 3 P( A B ) P( A ) P( B ) P( AB ) = + − = + − = 例6.任取一个两位数，求这个数能被2或3整除的概率

二.几何概型几何概型的两大特点：1、样本空间的样本点充满某个区域Q，月Q是可测的（即样本空间Q的测度m（Q）可用长度、面积或体积等几何度量来度量其“大小值））2、试验中等测度的事件发生的概率相等定理设E是按测度等可能概型（几何概型），m(Q）是样本空间的测度，m(A）是事件A的测度，则事件A发生的概率 : P(A)= m(A)m(2)NKDProbabilityand Statistics

Probability and Statistics （NKD） 二.几何概型 1 m “ ” .     、样本空间的样本点充满某个区域 ，且 是可测的 （即样本空间 的测度（ ）可用长度、面积或体积 等几何度量来度量其 大小 值）） 几何概型的两大特点： . 2、 试验中等测度的事件发生的概率相等. m( )  m( A ) 定理设E是按测度等可能概型（几何概型）， 是样本空间的测度， 是事件A的测度，则事件A 发生的概率： ( ) ( ) ( ) m A P A m = 

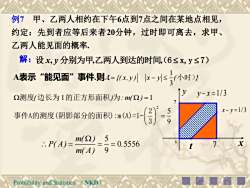
例7甲、乙两人相约在下午6点到7点之间在某地点相见，约定：先到者应等后来者20分钟，过时即可离去，求甲、乙两人能见面的概率解：设x,分别为甲,乙两人到达的时间,（6≤x,y≤7)A表示“能见面”事件.则A=(x,y)|x-≤(小时))yy-x=1/3Q测度(边长为1的正方形面积)为:m(Q)=17(2)5x-y=1/3事件A的测度（阴影部分的面积）：m（A）=1395m(2)6x=0.5556P(Af9m(A)NKDProbabilityand Statistics

Probability and Statistics （NKD） 例7 甲、乙两人相约在下午6点到7点之间在某地点相见， 约定：先到者应等后来者20分钟，过时即可离去，求甲、 乙两人能见面的概率. 解： 设 x y, , , 分别为甲乙两人到达的时间（6 x,y 7   ） A表示“能见面”事件.则： 1 3 A {( x, y ) x y ( } = −  小时） 2 1 1 5 9   = ( ) : m( )     =   测度 边长为 的正方形面积 为 2 事件A的测度(阴影部分的面积):m(A)=1- 3 5 0 5556 9 m( ) P( A ) . m( A )   = = = x 6 y y x − =1/ 3x y − =1/ 3 • t 7 7