《概率论与数理统计》课程教学课件（PPT讲稿）第三章 随机向量及其分布 3.1 二维随机变量的概率分布

第三章随机向量及其分布3.1二维随机变量的概率分布3.2 边缘分布3.3条件分布3.4 随机变量的独立性

3.1 二维随机变量的概率分布 3.2 边缘分布 3.4 随机变量的独立性 3.3 条件分布 第三章 随机向量及其分布

二维随机向量同一维随机变量一样，为了把某些试验的结果数量化有时需要用二维随机变量或二维随机向量（XY来描述。如实例1炮弹的弹着点的位置(X,Y就是一个二维随机变量。实例2考查某一地区学龄前儿童的发育情况，则儿童的身高H和体重W就构成二维随机变量（H,W）

同一维随机变量一样, 为了把某些试验的结果数量化, 有时需要用二维随机变量或二维随机向量(X,Y)来描述．如 二维随机向量 实例1 炮弹的弹着点 的位置(X,Y)就是一个二维 随机变量. 实例2 考查某一地区学龄前儿童的 发育情况, 则儿童的身高H和体重W就构 成二维随机变量(H,W)

1定义：设E是一个随机试验(x(e),Y(e)样本空间S=lel：设X-X（e）和Y-Y（e）是定义在S上的随机变量，由它们构成的向量exS(XY)叫做二维随机向量或二维随机变量。思考：根据这个定义，上例中张三的身高X和李四的体重Y能构成二维随机向量XY）吗？

定义：设E是一个随机试验， 样本空间S={e}；设X=X (e) 和Y=Y (e)是定义在S上的随 机变量，由它们构成的向量 (X,Y)叫做二维随机向量或二 维随机变量。 S e y ( X e Y e ( ), ( )) x 思考：根据这个定义，上例中张三的身高X和 李四的体重Y能构成二维随机向量(X,Y)吗？

3.1 二维随机变量的概率分布二维随机变量的分布函数二、二维离散型随机变量及其分布三、二维连续型随机变量及其分布

一、二维随机变量的分布函数 二、二维离散型随机变量及其分布 三、二维连续型随机变量及其分布 3.1 二维随机变量的概率分布

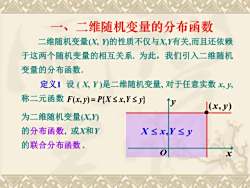
一、二维随机变量的分布函数二维随机变量(X，Y的性质不仅与X,Y有关，而且还依赖于这两个随机变量的相互关系.为此，我们引入二维随机变量的分布函数定义1设（X,Y)是二维随机变量，对于任意实数x,y，称二元函数F(x,y)=P(X≤x,Y≤)TyI(x,y)为二维随机变量（X,Y）的分布函数，或X和YX<x,Y≤y的联合分布函数O

二维随机变量(X, Y)的性质不仅与X,Y有关,而且还依赖 于这两个随机变量的相互关系. 为此，我们引入二维随机 变量的分布函数． 定义1 设 ( X, Y )是二维随机变量, 对于任意实数 x, y, 称二元函数 为二维随机变量(X,Y) 的分布函数, 或X和Y 的联合分布函数． F(x, y) = P{X  x,Y  y} O x y (x, y) • X  x,Y  y 一、二维随机变量的分布函数

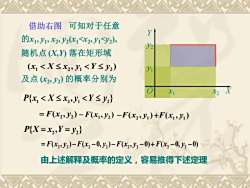
可知对于任意借助右图Y的x1, J1, X2, y2(xiy2),y2随机点（X,Y）落在矩形域(x<X≤x2,y<Y≤y2)Ji及点（x2,y2）的概率分别为 XOxiP(x, <X≤x,y<Y≤y2)= F(x2,y2) -F(xi,y2) -F(x2,y/)+F(X1,yr)P(X =X2,Y = y2)=F(x2,J2)-F(x2 -0, y2)-F(x2,J2 -0)+F(x2 -0, y2 -0)由上述解释及概率的定义，容易推得下述定理

2 1 −F x y ( , ) 及点 (x2 , y2 ) 的概率分别为 的x1 , y1 , x2 , y2 (x1<x2 , y1<y2 ), 随机点 (X,Y) 落在矩形域 借助右图 ( , ) 1 2 1 2 x  X  x y Y  y { , } 1 2 1 2 P x  X  x y  Y  y ( , ) 2 2 = F x y 可知对于任意 { , } 2 2 P X = x Y = y ( , ) ( 0, ) ( , 0) ( 0, 0) = F x2 y2 −F x2 − y2 −F x2 y2 − + F x2 − y2 − ( , ) 1 2 − F x y 1 1 +F x y ( , ) Y y2 y1 O x1 x2 X 由上述解释及概率的定义，容易推得下述定理

定理1分布函数F（xJ）具有下列性质：1°（有界性）对任意的实数x.y有0≤F(x,y)≤1, F(+0,+o) =1F(-00, y) = F(x,-00) = F(-00,-00) = 02°（单调性）F(xy）是x和y的单调不减函数Vy,有F(xi,y)≤F(x2,y)(x) <x2)Vx, 有F(x, y)≤F(x, y2) (yi< y2)3°（右连续性）F（x,）关于x和y都是右连续的：Vx, y,有F(x+0, y) = F(x, y), F(x, y+O)= F(x,y)反过来，满足上述性质的F（x，）也必定是某个二维随机变量的分布函数，因此：函数F(x，J）完整地描述了二维随机变量的概率分布

定理1 0 ( , ) 1, ( , ) 1 ( , ) ( , ) ( , ) 0 F x y F F y F x F   + + = − = − = − − = 分布函数 F (x, y) 具有下列性质： 1（有界性） 对任意的实数 x, y, 有 2（单调性）F(x, y) 是 x 和 y 的单调不减函数: 3（右连续性）F(x, y) 关于 x 和 y 都是右连续的: , ( , ) ( , ) ( ) , ( , ) ( , ) ( ) 1 2 1 2 1 2 1 2 x F x y F x y y y y F x y F x y x x       有 有 x, y,有F(x + 0, y) = F(x, y), F(x, y + 0) = F(x, y) 反过来, 满足上述性质的 F (x, y) 也必定是某个二维随 机变量的分布函数, 因此： 函数 F(x, y) 完整地描述了二维随机变量的概率分布

二、二维离散型随机变量及其分布若二维随机变量（X，Y）所取的可能值是有限对或可列多对，则称（X，Y）为二维离散型随机变量设(X,Y)所有可能取的值为(x,,y,),i,j=1,2,,记P(X = xi, Y = y,} = Pij, i, j=1,2,...则称此为(X,Y）的分布律,或X与 Y的联合分布律同一维一样，二维随机变量的分布律满足：P,≥0Pi,是某个二维随机变量（X,Y)的分NMPi =1布律通常我们用分布律表示二维随机变量的概率分布

设(X,Y )所有可能取的值为(xi , y j ),i, j = 1,2,  ,记 若二维随机变量 ( X, Y ) 所取的可能值是有限对或可列 多对,则称 ( X, Y ) 为二维离散型随机变量 二、二维离散型随机变量及其分布 则称此为(X, Y ) 的分布律,或X与 Y 的联合分布律 pi j 是某个二维随 机变量(X,Y)的分 布律 1 0 1 1 =    =  i j= ij ij p p P{X = xi ,Y = y j } = pi j , i, j = 1,2,  同一维一样, 二维随机变量的分布律满足： 通常我们用分布律表示二维随机变量的概率分布

二维随机变量（XY）的分布律也可用表格表示为：YyiJ2yiX有了二维离散XPi1P12Puj型随机变量的X2P21P22P2j...三三分布律 pij,就x;PiiPi2Pij能容易的得到..1..ZPI(X,Y) eG) =P(X=X,,Y=y,}=Pij(xy,)EG(Xy,)EGMF(x,J)=P(X=X,,Y=y,=Pijx,Sx,yjSyx,Sx,yjSyPij, =F(x,J,)-F(x, -0,y,)-F(x,J, -0)+F(x, -0,y, -0)

二维随机变量( X,Y ) 的分布律也可用表格表示为： X Y y1 y2  yi    xi x x 2 1 p11 p12  p1 j  p21 p22  p2 j  pi1 pi 2  pi j     , , ( , ) { , } i j i j i j i j x x y y x x y y F x y P X x Y y p     = = = =   ( , ) ( 0, ) ( , 0) ( 0, 0) p F x y F x y F x y F x y i j i j i j i j i j = − − − − + − − ( , ) ( , ) {( , ) } { , } i j i j i j i j x y G x y G P X Y G P X x Y y p    = = = =   有了二维离散 型随机变量的 分布律 pij , 就 能容易的得到

例从一个装有3支蓝色、2支红色、3支绿色圆珠笔的盒子里，随机抽取两支，若X、Y分别表示抽出的蓝笔数和红笔数，求（XY）的分布律解（X,Y）所取的可能值是(0,0), (0,1),(1,0), (1,1), (0,2),(2,0)故所求分布律为YT2XP(X =i,Y =j)03/281/286/28CiC,c2-i-j19/286/280C0023/28(i+ j≤2,i, j=0,1,2)

例 ( X,Y ) 所取的可能值是 (0,0), 解 (0,1),(1,0), (1,1),(0,2),(2,0) P X i Y j { , } = = 2 3 2 3 2 8 i j i j C C C C − − = 从一个装有3支蓝色、2支红色、3支绿色圆珠笔 的盒子里, 随机抽取两支, 若 X、Y 分别表示抽出的蓝笔 数和红笔数,求(X,Y )的分布律. ( 2, , 0,1,2) i j i j +  = 3 28 9 28 3 28 6/ 28 0 1 28 0 0 X Y 0 1 2 0 1 2 6/ 28 故所求分布律为