《概率论与数理统计》课程教学课件（PPT讲稿）第六章 大数定律和中心极限定理 6.2 中心极限定理

中心极限定理6.2测人们发现：大量的随机变量都服从正态分布，例如：量误差、身高、体重、产品的直径、长度、重量、高度等都近似服从正态分布因此，人们自然要问：为什么这些变量会服从正态分布呢？这是因为这些变量是由大量的相互独立的随机因素的综合影响所形成的，而其中每一个因素在总的影响中所起的作用都是微小的。在概率论中，我们把有关论证随机变量之和的极限分布的一系列定理叫做中心极限定理

人们发现：大量的随机变量都服从正态分布, 例如：测 量误差、 身高、体重 、 产品的直径、长度、重量、高度 等都近似服从正态分布. 6.2 中心极限定理 在概率论中，我们把有关论证随机变量之和的极限分 布的一系列定理叫做中心极限定理. 因此, 人们自然要问：为什么这些变量会服从正态分 布呢？ 这是因为这些变量是由大量的相互独立的随机因素的 综合影响所形成的，而其中每一个因素在总的影响中所起 的作用都是微小的

定理1（林德伯格-列维中心极限定理设随机变量X,X,.,X相互独立，服从同一分布，且具有数学期望和方差E(X,)= μ,D(Xr) =α >0 (k =1,2,...)则随机变量和Y,=ZX,的标准化和k=12xx-nY,-EYk=lDYNng的分布函数F（x）的极限是标准正态分布函数@（x）.即对任意的x有-e2dtlim F,(x)= lim P(Z, ≤ x) = @(x) = J。-Ln-0n80

定理1 ( ) ( ). F n 的 分 布 函 数 x 的 极 限 是 标 准 正 态 分 布 函 数  x 即 对 （林德伯格-列维中心极限定理） 1 2 , , , , , , 设随机变量 X X  X n 相互独立 服从同一分布 且具有数学期望和方差 n n n n Y EY Z DY     n X n n k k   1 则随机变量和 ( ) , ( ) 0 ( 1,2, ) E Xk   D Xk   2  k    的标准化和   n k Yn Xk 1 任意的 x 有 lim F (x) lim P{Z x} (x) n n n n      2 2 1 e d 2π t x t    

定理1表明：无论各个随机变量X，X，服从什么分布，只要它们服从同一分布且相互独立，那么它们的和，当n很大时，就近似地服从正态分布。即有ZX,-nu近似近似N(O,1), Y, =Zx, N(nμ,ng")Eavn咖

定理1表明:无论各个随机变量 X1 , X2 , . 服从什么分 布, 只要它们服从同一分布且相互独立, 那么它们的和, 当n 很大时, 就近似地服从正态分布．即有 1 2 1 ~ (0 ,1), ~ ( , ) n k n k n n k k X n Z N Y X N n n n            近似 近似

例1：计算机进行加法计算时，把每个加数取为最接近于它的整数来计算。设所有的舍入误差是相互独立的随机变量，并目都在区间（-0.5.0.51上服从均匀分布，求300个数相加误差总和的绝对值不超过10的概率。解设随机变量X表示第i个加数的舍入误差，则在区间(-0.5,0.51上服从均匀分布，从而EX, = 0, DX,(i = 1,2, ...)12300Zx,-0由定理1知近似成立X~ N(0,1)5/300/12i=l300300P≤10/=P)-2≤ZZX所以X≤25=i=l~ Φ(2)- Φ(- 2) = 2Φ(2)-1 = 0.9544U

例1：计算机进行加法计算时，把每个加数取为最接近于它的 整数来计算。设所有的舍入误差是相互独立的随机变量，并且 都在区间 上服从均匀分布，求300个数相加误差总和 的绝对值不超过10的概率。 解 设随机变量 表示第 个加数的舍入误差，则在区间 上服从均匀分布，从而 由定理1知 近似成立 所以 (0.5,0.5] Xi i (0.5,0.5] ( 1,2, ) 12 1 EX i  0 , DX i  i   ~ (0,1) 300 12 0 5 1 300 1 300 1 N X X i i i i                           2 5 1 10 2 300 1 300 1 i i i P X i P X  2   2  22  1  0.9544

如果把定理1中的X看成n重伯努利试验中第i次试验时A发生的次数（即X,服从0-1分布）并记P(A)=P，则Y, = EX, ~ B(n, p), EY, = np, DY, = np(1- p)k=1于是定理1可表现为如下的定理2的形式

如果把定理1中的Xi看成 n重伯努利试验中第 i 次试验 时A发生的次数（即Xi服从0-1分布）并记 P(A)=p, 则 于是定理1可表现为如下的定理 2的形式 1 ~ ( , ), n n k k Y X B n p    EY np, n  DY np(1 p) n  

定理2（棣莫弗一拉普拉斯定理设随机变量Y,~B(n,p)则对于任意x，恒有Y, - nplim P dt =@Φ(x)-0<xn-00Vnp(1- p)T定理2表明：二项分布的极限分布是正态分布，当n充分大时，可以利用该定理来计算二项分布的概率亦即，若X~Bn，p），则当n充分大时近似近似X-np或X~N(np,np(l-p))N(O,1)np(1-p)X-npD≤b=@(b)-Φ(a)a/np(1-p)

定理（2 棣莫弗－拉普拉斯定理） 则 对于任意 x, 恒有 2 2 1 lim d ( ) (1 ) 2π t x n n Y np P x e t x np p                   ~ ( , ), 设随机变量Y n B n p 亦即,若X ~ B(n , p ), 则当n充分大时 定理2表明: 二项分布的极限分布是正态分布, 当n充分 大时, 可以利用该定理来计算二项分布的概率. X ~ N(np ,np(1  p)) 近似 ~ (0 ,1) 或 (1 ) X np N np p   近似 ( ) ( ) (1 ) X np P a b b a np p                

例2：某工厂有200台同类型的机器，每台机器工作时需要的电功率为O千瓦。由于工艺等原因，每台机器的实际工作时间只占全部工作时间的75%。假定各台机器能否正常工作是相互独立的，求：任一时刻有144--160台机器正在工作的概率；解设X表示任意时刻正在工作的机器数，则X～B(n,p）故由定理2及n =200，P=0.75知X-npX -150~N(0,)近似成立V37.5/np(1 - p)从而有任意时刻有144160台机器正在工作的概率为10X-15027P(143 < X ≤160)= PV37.537.5V37.5~ @(1.63) - @Φ(-1.14)= Φ(1.63) - 1 + Φ(1.14)=0.9484-1+0.8729=0.8213

例2 ：某工厂有200台同类型的机器，每台机器工作时需要的电 功率为 千瓦。由于工艺等原因，每台机器的实际工作时间只 占全部工作时间的 。假定各台机器能否正常工作是相互独 立的，求：任一时刻有144-160台机器正在工作的概率； 解 设 表示任意时刻正在工作的机器数，则 故由定理2及 知 近似成立 从而有任意时刻有144~160台机器正在工作的概率为 Q 75% X ~ B(n, p) X n  200 , p  0.75 ~ (0,1) 37.5 150 (1 ) N X np p X np                    37.5 10 37.5 150 37.5 7 143 160 X P X P  1.63   1.14   1.63  1  1.14   0.9484  1  0.8729  0.8213

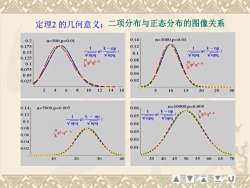
定理2的几何意义：二项分布与正态分布的图像关系0.14n=1000.p=0.010.2n=500,p=0.010.1750.12k-npnp00.150.1VnpqynpqVnpgVnpg0.1250.08Opiqn-kDpkqa-k0.10.060.0750.040.050.020.02528101246165152025301410n=10000,p=0.005n=5000.p=0.0050.060.14Knpk0.1210.05npgVnpg0.1npanpg0.040.080.03p0.060.020.040.010.02203040354045505560657010

定理2 的几何意义：二项分布与正态分布的图像关系