《复变函数与积分变换》课程教学资源（PPT课件）第一章 复数与复变函数 1.3 第三节 复数的乘幂与方根

复变函数第三节复数的乘幂与方根一、乘积与商二、 幂与根三、小结与思考-U

第三节 复数的乘幂与方根 一、乘积与商 二、幂与根 三、小结与思考

复变函数一、乘积与商定理一两个复数乘积的模等于它们的模的乘积；两个复数乘积的辐角等于它们的辐角的和证设复数z,和z2的三角形式分别为zi =ri(cosa +isinQ),Z2 =rz(cos02 +isin0,)则z : Z2 =ri(cos, + isin@))·r2(cos , + isin 02)= ri · r2[(cos, cos , sin Q, sin ,)+ i(sin e, cos , + cos, sin 0,))u

2 一、乘积与商 定理一 两个复数乘积的模等于它们的模的乘 积; 两个复数乘积的辐角等于它们的辐角的和. 设复数z1和z2的三角形式分别为 (cos sin , z1 = r1 1 + i 1） (cos sin , z2 = r2  2 + i  2） (cos sin ) (cos sin ) 1 2 1 1 1 2  2  2 则z z = r + i r + i (sin cos cos sin )] [(cos cos sin sin ) 1 2 1 2 1 2 1 2 1 2         + + =  − i r r 证

复变函数zi ·Z2 = ri ·r[cos(e, +02) + isin(① +0,)][证毕]Arg(ziz2) = Argzi +Argz2从几何上看，两复数对应的向量分别为，z2，先把按逆时针方向旋转一个角21511再把它的模扩大到倍0Z2O所得向量之就表示积 Z1·Z2·+x0辐角相加两复数相乘就是把模数相乘u

3 [cos( ) sin( )] 1 2 1 2 1 + 2 + 1 + 2 z z = r r i 两复数相乘就是把模数相乘, 辐角相加. , 再把它的模扩大到r2 倍 从几何上看, 两复数对应的向量分别为 , , 1 2 z z   , 2 1 旋转一个角 先把 z 按逆时针方向  . 1 2 所得向量 z 就表示积 z z   2  o x y r 2r 1r • 2 z 1  • 1z • z Arg( ) Arg Arg . 1 2 1 2 z z = z + z [证毕]

复变函数说明由于辐角的多值性,Arg(zz2)= Argzi +Argzz两端都是无穷多个数构成的两个数集对于左端的任一值，右端必有值与它相对应例如，设z=-1，2=i，则 ·Z2 =-i,Argz = 元+2nπ，(n = 0,±1, ±2,..),元Argz2+2m元,(m= 0,±1, ±2,.)?2元+2k元,Arg(zz2)(k = 0, ±1, ±2,:)12+一3元元故只须k=m+n+l.+2k元,+ 2(m+n)元 =22若k=-1,则m= 0,n=-2或m=-2,n= 0U

4 说明 由于辐角的多值性, 1 2 Arg 1 Arg 2 Arg(z z ) = z + z 两端都是无穷多个数构成的两个数集. 对于左端的任一值, 右端必有值与它相对应. 例如， 1, , 1 2 设 z = − z = i , 1 2 则 z z = −i Arg 2 , ( 0, 1, 2, ), z1 =  + n n =    2 , ( 0, 1, 2, ), 2 Arg 2 +  =     z = m m 2 π, ( 0, 1, 2, ), 2 π Arg( ) z1 z2 = − + k k =    2 , 1. 2 2( ) 2 3 +  = + +  + +  = −  故 m n k 只须 k m n 若k = −1, 则m = 0,n = −2或m = −2,n = 0

复变函数设复数z和z的指数形式分别为i(0 +02)Z =reio, = rei,，则z Z=i e由此可将结论推广到n个复数相乘的情况：设 zk = r(cos0k +isinOk)= reiok, (k =1,2,*,n)Zi.Z2..... Zn = ri. r...n[cos(o, +0, +...+on)+ isin(e +, +...+0n))= ri 2.... ,ei(++,+.,)U

5 设复数z1和z2的指数形式分别为 , 1 1 1 i z = r e . ( ) 1 2 1 2 1+ 2  =  i , 则 z z r r e 2 2 2 i z = r e 由此可将结论推广到 n 个复数相乘的情况: n z z z 1 2 z r (cos isin ) r e , (k 1,2, ,n) k i 设 k = k  k +  k = k  =  sin( )] [cos( ) 1 2 1 2 1 2 n n n i r r r       + + + + =  + + +    . ( ) 1 2 1 2 n i n r r r e   + + =   

复变函数两个复数的商的模等于它们的模的商：两定理二个复数的商的辐角等于被除数与除数的辐角之差按照商的定义，当21#0时，z2=孕Z1,证Z17212Argz2 = Arg+ Argz1'Z72Z1Z1Z172Z2N于是Arg= Argz2 - Argz1Z1KZ1设复数z,和z,的指数形式分别为Z1 =rieio,，Z2 = rei0,, 则2= ei(2,-2),i0,[证毕]Z1riU

6 定理二 两个复数的商的模等于它们的模的商; 两 个复数的商的辐角等于被除数与除数的辐角之差. 证 按照商的定义, 0 , 当z1  时 , 1 1 2 2 z z z z = , 1 1 2 2 z z z z = Arg Arg Arg , 1 1 2 2 z z z z  +      = , 1 2 1 2 z z z z 于是 = Arg Arg Arg . 2 1 1 2 z z z z  = −      设复数z1和z2的指数形式分别为 , 1 1 1 i z = r e . ( ) 1 2 1 2  2−1 = i e r r z z z2 = r2 e i 2 , 则 [证毕]

复变函数元元(1- ~/3i),例1 已知icos， Zz = sinZ1二33求Z: 和Z.2元-3元-3解因为 z = cos+isinRC元+isinZ2 = cOS6)元元元元=-i,所以 z1: Z2 = COS+isin3636V3元元元元Z1+isin=cos一332266Z2U

7 例 1 解 , 3 cos 3 (1 3 ), sin 21 1 2  −  已知 z = − i z = i , 3 sin 3 cos 1     + −    因为 z = − i , 6 sin 6 cos 2     + −    z = − i    −   + −    −   = − 3 6 sin 3 6 cos 1 2 所以 z z i = − i ,    +   + −    +  = − 3 6 sin 3 6 cos 21 i zz . 21 23 = − i . 21 1 2 zz 求 z z 和

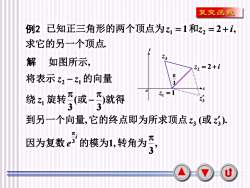
复变函数例2 已知正三角形的两个顶点为z =1和z2=2+i求它的另一个顶点13解如图所示,Z2 =2 +i元-3将表示 z2 -z的向量+x=1ZZ3绕旋转(或-)就得33到另一个向量,它的终点即为所求顶点 (或)元元-3因为复数e3 的模为1,转角为u

8 例2 解 . 1 2 , 1 2 求它的另一个顶点 已知正三角形的两个顶点为z = 和z = + i , ( ). ) 3 ( 3 3 3 1 2 1 z z z z z   −  − 到另一个向量 它的终点即为所求顶点 或 绕 旋转 或 就得 将表示 的向量 如图所示, o x y z1 = 1 z = 2 + i 2 3 z 3 z  3  , 3 1, 3   因为复数 的模为 转角为 i e

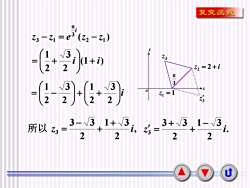
复变函数元i1=e3(Z2 - Zl)Z3 - Z1y+15311小+(1 +i)22Z2 = 2+i元-3(6-9)(+)+x0=1Z1Z31+~33-V33+/3/3LIV所以 z3 1.Z3十1/2222U

9 ( ) 2 1 3 3 1 z z e z z i − = −  o x y z1 = 1 z = 2 + i 2 3 z 3 z  3  (1 ) 2 3 2 1 i + i      = + i       + +      = − 2 3 2 1 2 3 2 1 , 2 1 3 2 3 3 3 z i + + − 所以 = . 2 1 3 2 3 3 3 z i − + +  =

复变函数二、幂与根1.n次幂：n个相同复数z的乘积称为z的n次幂记作z"，"=zn个对于任何正整数n,有zn=rn(cosne+isinnの)那么当n为负整数时如果我们定义z-n上式仍成立u

10 二、幂与根 1. n次幂: , , n z n z z n 记 作 个相同复数 的乘积称为 的 次 幂  . n个 n z = zz z n, z r (cos n isin n ). n n 对于任何正整数 有 = + . , , 1 上式仍成立 如果我们定义 那么当n为负整数时 z z n n = −