《复变函数与积分变换》课程教学资源（PPT课件）第一章 复数与复变函数 1.6 第六节 复变函数的极限和连续性

复变函数第六节复变函数的极限和连续性函数的极限一、#二、函数的连续性三、小结与思考U

第六节 复变函数的极限 和连续性 一、函数的极限 二、函数的连续性 三、小结与思考

复变函数一、函数的极限1.函数极限的定义：设函数w=f(z)定义在z的去心邻域00,相应地必有一正数S(8)使得当0<zol(0<≤)时,有(z)A<那末称A为f(z)当z趋向于z时的极限记作 lim f(z)= A.(或 f(z)-0→A)7Z0注意：定义中z→的方式是任意的U

2 一、函数的极限 1.函数极限的定义: ( ) . 0 (0 ) , ( ) 0, ( ) 0 , , ( ) 0 0 0 0 那末称 为 当 趋向于 时的极限 使得当 时 有 对于任意给定的 相应地必有一正数 内 如果有一确定的数 存 在 设函数 定义在 的去心邻域 A f z z z z z f z A z z A w f z z          −    −    −  = lim ( ) .( ( ) ) 0 0 f z A f z A z z z z = ⎯ →⎯→ → 记作 或 注意: . 定义中z → z0的方式是任意的

复变函数2.极限计算的定理定理一设 f(z) =u(x,y)+iv(x,y), A=uo +ivo)Zo=Xo+iyo,那末lim f(z)=A的充要条件是Z→Z0lim u(x,y) = uolim v(x, y) = Vox-→xox-→xoy-→yoy-→yo证((1) 必要性.如果 lim f(z) = A,Z→Zo根据极限的定义当0<(x+ijy)-(x+iyo)<S时,(u+iv)-(uo +ivo)<8,u

3 2. 极限计算的定理 定理一 lim ( , ) , lim ( , ) . , lim ( ) ( ) ( , ) ( , ), , 0 0 0 0 0 0 0 0 0 0 0 0 u x y u v x y v z x iy f z A f z u x y iv x y A u iv y y x x y y x x z z = = = + = = + = + → → → → → 那 末 的充要条件是 设 证 lim ( ) , 0 f z A z z = → 如果 根据极限的定义 0 ( ) ( ) , 当  x + iy − x0 + iy0   时 ( ) ( ) , 0 0 u + iv − u + iv   (1) 必要性

复变函数或当 0</(x-x)2+(y-yo)2<s时,(u-uo)+i(v-vo)<, = u-uol<, -Vo<,故 lim u(x,y)=uo,lim v(x, y) = Vo.x-→xox-→xoy-→yoy-→yo(2) 充分性. 若 lim u(x,y)= uo,lim v(x,y) = Vosx-→Xox-→xoy-→yoy-yo那么当 0<(x-xo)2+(y-yo)2<时,812c12有u-uo<v-VoU

4 0 ( ) ( ) , 2 0 2 或当  x − x0 + y − y   时 ( ) ( ) , 0 0 u − u + i v − v   , , 0 0  u − u   v − v   lim ( , ) , lim ( , ) . 0 0 0 0 0 0 u x y u v x y v y y x x y y x x = = → → → → 故 lim ( , ) , lim ( , ) , 0 0 0 0 0 0 u x y u v x y v y y x x y y x x = = → → → → 若 0 ( ) ( ) , 2 0 2 那么当  x − x0 + y − y   时 (2) 充分性. , 2 , 2 0 0   有 u − u  v − v 

复变函数f(z)- A = (u-uo)+i(v-Vo)≤u-uo +v-vo故当 <zol<时，f(z)-A<ε,所以 lim f(z)= A.[证毕]Z-→Z0说明该定理将求复变函数 f(z)=u(x,y)+iv(x,y)的极限问题,转化为求两个二元实变函数u(x,J)和(x,y)的极限问题u

5 ( ) ( ) ( ) 0 0 f z − A = u − u + i v − v 0 0  u − u + v − v 0 , 故当  z − z0   时 f (z) − A   , lim ( ) . 0 f z A z z = → 所以 [证毕 ] 说明( , ) . , ( , ) ( ) ( , ) ( , ) 和 的极限问题 的极限问题 转化为求两个二元实变函数 该定理将求复变函数 v x y u x y f z = u x y + iv x y

复变函数定理二设 lim f(z) = A, lim g(z)= B,那末ZZOZ→Z0(1) lim[f(z)±g(z)) = A± B;Z→ZO(2)1lim[f(z)g(z)] = AB;Z-→ZoAf(z)lim(3)(B ± 0).Bg(z)z>Z0与实变函数的极限运算法则类似u

6 定理二 ( 0). ( ) ( ) (3) lim (2) lim[ ( ) ( )] ; (1) lim[ ( ) ( )] ; lim ( ) , lim ( ) , 0 0 0 0 0 =  =  =  = = → → → → → B B A g z f z f z g z AB f z g z A B f z A g z B z z z z z z z z z z 设 那 末 与实变函数的极限运算法则类似

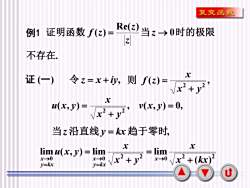
复变函数Re(z)当→0时的极限例1 证明函数 f(z)=N不存在。x证(一)令z=x+iy，则 f(z)=2Vx? + yxu(x,y) =v(x,y) = 0,x?+ y?当z沿直线y=kx趋于零时，xxlim u(x, y) = limlim222x-→0x-0x-0+(kx)Vx+yXy=kry=kxU

7 例 1 证 ( 一 ) . 0 Re( ) ( ) 不存在 证明函数 = 当z → 时的极限 z z f z 令 z = x + iy, ( ) , 2 2 x y x f z + 则 = ( , ) , ( , ) 0, 2 2 = + = v x y x y x u x y 当z 沿直线 y = kx 趋于零时, 2 2 0 0 lim ( , ) lim x y x u x y y k x x y k x x + = =→ =→ 2 2 0 ( ) lim x kx x x + = →

复变函数1x= lim=±V1+k?x-0 /x2(1+k2)随k值的变化而变化lim v(x, y) = 0,所以 lim u(x,y)不存在,x-→xox-→xoy-→yoy-→yolim f(z)不存在。根据定理一可知,z0证(二)令 z = r(coso+isinの),rcosa则 f(z)==cos,U

8 (1 ) lim 2 2 0 x k x x + = → , 1 1 2 + k =  随k 值的变化而变化, lim ( , ) , 0 0 所以 u x y 不存在 y y x x → → lim ( , ) 0, 0 0 = → → v x y y y x x 根据定理一可知, lim ( ) . 0 f z 不存在 z→ 证 (二) 令 z = r(cos + isin ), r r f z cos 则 ( ) = = cos

复变函数当z沿不同的射线argz=θ趋于零时,f(z)趋于不同的值例如z沿正实轴argz=0趋于零时，f(z)→l元一沿argz=趋于零时，(z)→0,2故 limnf(z)不存在Z-0u

9 当z 沿不同的射线 argz = 趋于零时, f (z)趋于不同的值. 例如z 沿正实轴argz = 0趋于零时, f (z) →1, , 2 π 沿arg z = 趋于零时 f (z) → 0, lim ( ) . 0 故 f z 不存在 z→

复变函数例2 证明函数 f(z)=(z0)当→0时的极Z限不存在。证令z=x+iy,f(z)=u+iv,2xyx2 - J2则 u(x,y):v(x,y) =x? + j2,x? + y2当z沿直线y=kx趋于零时2k2xylim v(x, y) = lim1+k2,x-0 x2 + y2x-0y=kxy=kxU

10 例 2 证 . ( ) ( 0) 0 限不存在 证明函数 = z  当 z → 时的极 zz f z 令 z = x + iy, f (z) = u + iv, ( , ) , 2 2 2 2 x y x y u x y +− 则 = , 2 ( , ) 2 2 x y xy v x y + = 当z 沿直线 y = kx 趋于零时, 2 2 0 0 2 lim ( , ) lim x y xy v x y y k x x y k x x + = =→ =→ , 1 2 2 kk + =