《概率论与数理统计》课程教学课件（PPT讲稿）第三章 随机向量及其分布 3.3 条件分布

条件分布3.3二维随机变量(X,Y)作为一个整体，具有联合概率分布，其中的X或Y作为单个随机变量，具有边缘概率分布有时，我们要考虑在其中一个随机变量取得（可能的）固定值的条件下另一随机变量的概率分布.这样得到的X或Y的概率分布叫做条件概率分布，简称条件分布

3.3 条件分布 二维随机变量(X,Y )作为一个整体, 具有联合概 率分布,其中的X或Y作为单个随机变量, 具有边缘概 率分布. 能的) 固定值的条件下, 另一随机变量的概率分 布. 这样得到的X或Y的概 率分布叫做条件概率分 布, 简称条件分布． 有时, 我们要考虑在其中一个随机变量取得 (可

设二维离散型随机变量的联合分布律为P(X = x,Y = y,} = Pi, (i, j = 1,2,..)则由条件概率计算公式可求得：1）（X,Y)在X=x的条件下Y的条件分布律为P(X=X,Y=y;_ Pij(i =1,2,)P(Y = y, I X =x,} =P(X = x;)Pi.(p..>0,i=1,2,..)2）(X,Y)在Y=y,的条件下X的条件分布律为P(X = x,Y = y, - Pii (i= 1,2,...)P(X = x;IY = y,} =P(Y = yj)p.j(p., > 0, j =1,2,..)

条件分布律为 P{X = x ,Y = y } = p (i, j = 1,2, ) i j i j 设二维离散型随机变量的联合分布律为 则由条件概率计算公式可求得: { | } j i P Y = y X = x • = i i j p p (i = 1,2, ) ( j = 1,2, ) { } { , } i i j P X x P X x Y y = = = = { | } i j P X = x Y = y { } { , } j i j P Y y P X x Y y = = = = j i j p p • = 2) (X,Y)在Y＝yj 的条件下X 的条件分布律为 1) (X,Y)在X＝xi的条件下Y的 (  0, = 1,2, ) • p j j (  0, = 1,2, ) • p i i

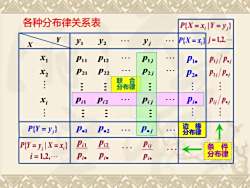
各种分布律关系表P(X=x, [Y =y)Yj=1,2,.P(X =x,)yiy2yjXXiP11PajP12Pi.Pu,/p.jP21P22P2jX2P2Pa; / P.j联命.分布律Pi.Piu/p.jPilXiPi2Pij··边缘P(Y = y,)p.12DT分布律PilP(Y = y,IX=x,)Di条件分布律i=1,2,..PiPi

联 合 分布律 边 缘 分布律 各种分布律关系表 i• i p p 1 i• i p p 2 i• i j p  p  j j p p 2 • j j p p 1 • i j j p p•   { | } i j P X = x Y = y { | } j i P Y = y X = x   p1• p2• pi• { }i P X = x P{Y = y j } p•1 p•2  p• j  i = 1,2,  j = 1,2,  条 件 分布律 X Y y1 y2  y j    xi x x 2 1 p1 1 p12  p1 j  p21 p22  p2 j     pi1 pi 2  pi j    

例1求3.1节例1中定义的(X,)在X=3的条件下Y的条件分布律以及在Y=3的条件下X的条件分布律Y解P(X=i|Y=3)2413Pi.X011/4001/40201/41/81/80由3.1节知31/121/121/41/124/701/43/71/161/1641/161/161337125Poj48484848现在条件1110P(Y=jlX=3)33分布律3

解 求3.1节例1中定义的(X,Y)在X=3的条件下Y 的条件分布律以及在Y=3的条件下X的条件分布律. 例1 P{X = i |Y = 3} P{Y = j | X = 3} 3 1 3 1 3 1 0 4/ 7 3/ 7 0 0 j 1 p• 48 25 48 13 48 7 48 3 i • p 1/ 4 1/ 4 1/ 4 1/ 4 X Y 1/ 4 1/ 8 1/12 1/16 0 1/ 8 1/12 1/16 0 1/12 1/16 0 0 1/16 1 2 3 4 1 2 3 4 0 0 条 件 分布律 由3.1 节知 由3.2 节知 现 在

例1解的写法解利用3.2节例1的联合与边缘分布律，可知随机向量(XY在X=3的条件下Y的条件分布律为23yj10P(Y = j|X =3)333随机向量(XY在Y=3的条件下X的条件分布律为23Xi4/73/700P(X =i|Y =3)

解 随机向量(X,Y)在X=3的条件下Y的条件分布律为 例1解的写法 P{X = i |Y = 3} P{Y = j | X = 3} 3 1 3 1 3 1 0 0 4/ 7 3/ 7 利用3.2节例1的联合与边缘分布律,可知 随机向量(X,Y)在Y=3的条件下X的条件分布律为 y j 1 2 3 4 0 xi 1 2 3 4

对于 具有密度 f(x,y)的连续型随机变量(X,Y)也有类似于离散型随机变量的条件分布：1)在fx(x)和f(x,y)的连续点二维随机变量(X,Y)在X=x的条件下Y的 条件分布密度为f(x,y)frix(y/x)=(fx(x) >0)fx(x)2)同样,在f(y)和f(x,y)的连续点随机变量(X,Y)在Y=y的条件下X的条件分布密度为f(x,y)Jxir(x/y)=(fr(y) >0)fr(y)

对于 具有密度 f (x, y) 的连续型随机变量 (X,Y ), ( ) ( , ) ( | ) | f x f x y f y x X Y X = ( f (x)  0) X 条件分布密度为 ( ) ( , ) ( | ) | f y f x y f x y Y X Y = ( f ( y)  0) Y 也有类似于离散型随机变量的条件分布： 1) 在f X (x)和f (x, y)的连续点,二维随机变量 (X,Y)在X = x的条件下Y的 2)同样,在f Y ( y)和f (x, y)的连续点,随机变量 (X,Y)在Y = y的条件下X的 条件分布密度为

与条件分布密度相应的有1)(X,Y)在X=x的条件下Y的条件分布函数：Fyx(yIx) = P([Y≤ j|X = x) = f Jrx(y/x)d y2)(X,Y)在Y=y的条件下X的条件分布函数:Fxir(x|y)= P(X ≤xY = y)= [-m fxir(x|y)dx联合分布、边缘分布、条件分布的关系边缘分布一联合分布联合分布条件分布

− =  = = y Y X Y X F ( y | x) P{Y y X x} f ( y | x)d y − =  = = x X Y X Y F (x | y) P{X xY y} f (x | y)d x 与条件分布密度相应的有 1)(X,Y)在X = x的条件下Y的 条件分布函数： 2)(X,Y)在Y = y的条件下X的 条件分布函数： 联合分布、边缘分布、条件分布的关系： 联合分布 边缘分布 条件分布 联合分布

例2求3.1节例2中(X,Y)在X=x(x>0)条件下Y的条件分布密度和Y=y(y>0）条件下X的条件分布密度[2e-(2x+y), x>0,y>0解由3.1节知f(x,J)=其它[0,-2x2ee-', y>0,x>0,fy(y) =1 fx(x)=由3.2节知[0,0,x≤0,J≤02e-(2x+y)f(x,y),y>0e故 fyix(y/x):2e-2x(x>0)fx(x)（条件密度）0,y≤O2e-(2x+y)f(x,y)-2x=2e,x>0fxir (x / y)ey(y>0)fr(y)[0,x≤0

解 求3.1节例2中(X,Y)在X=x (x>0)条件下Y的 条件分布密度和Y=y (y>0)条件下X的条件分布密度 例2 由3.1节知      = − + 0, 其它 2e , 0, 0 ( , ) (2 ) x y f x y x y      = − 0, 0, 2e , 0, ( ) 2 x x f x x X      = − 0, 0 e , 0 ( ) y y f y y Y ( ) ( , ) ( | ) | f x f x y f y x X Y X = ( ) ( , ) ( | ) | f y f x y f x y Y X Y = 故       =  = − − − + 0, 0 e , 0 2e 2e 2 (2 ) y y y x x y       =  = − − − + 0, 0 2e , 0 e 2e 2 (2 ) x x x y x y (x  0) ( y  0) 由3.2节知 (条件密度)

十例3设参加考研的学生，正常发挥的概率为a，超常发挥的概率为b，发挥失常的概率为c，a+b+c=1。设某班有10人参加考研，发挥正常的人数为X，发挥超常的人数为Y。求（1）（X，Y）的联合分布律：(2) P(X+Y>1) ;（3）在Y=3的条件下，X的分布律解：（1）X，Y的联合分布律为10!a'b'c10-i-jP(X = i,Y = j)= CloClo-,a'b'cl0-i-ji! j!(10-i-j)!i, j = 0,1,2,...,10; i+ j≤10

设参加考研的学生，正常发挥的概率 为a,超常发挥的概率为b，发挥失常的概率为 c，a+b+c=1。设某班有10人参加考研，发挥 正常的人数为X，发挥超常的人数为Y。求 （1）（X,Y)的联合分布律； （2）P(X+Y>1)； （3）在Y=3的条件下，X的分布律。 10 10 10 10 10! ( , ) ! !(10 )! , 0,1,2,.,10; 10. i j i j i j i j i j P X i Y j C C a b c a b c i i j i j i j i j − − − − = = = = − − − = +  解: (1)X, Y的联合分布律为 例3

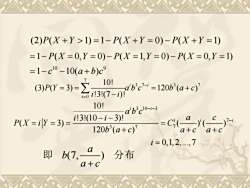
(2)P(X +Y >1)=1- P(X +Y = 0)- P(X +Y = 1)=1-P(X =0,Y = 0)- P(X =1,Y =0)- P(X = 0,Y =1)=1-cl0 -10(a+b)c710!a'b3c7-i =120b'(a+c)(3)P(Y = 3) = i13!(7-i)!10!α'b3c10-i-3i!3!(10-i-3)!aP(X =iY = 3) ==C)(120b'(a+c)a+ca+ci = 0,1,2,., 7a即 分布b(7)a+c

(2) ( 1) 1 ( 0) ( 1) P X Y P X Y P X Y +  = − + = − + = 10 9 1 ( 0, 0) ( 1, 0) ( 0, 1) 1 10( ) P X Y P X Y P X Y c a b c = − = = − = = − = = = − − + 7 3 7 3 7 0 10! (3) ( 3) 120 ( ) !3!(7 )! i i i P Y a b c b a c i i − = = = = + −  3 10 3 7 3 7 7 10! !3!(10 3)! ( 3) ( ) ( ) 120 ( ) 0,1,2,.,7 i i i i i a b c i i a c P X i Y C b a c a c a c i − − − − − = = = = + + + = (7, ) a b a c + 即 分布