《复变函数与积分变换》课程教学资源（PPT课件）第一章 复数与复变函数 1.5 第五节 复变函数

复变函数第五节复变函数一、复变函数的定义二、映射的概念三、典型例题四、小结与思考U

第五节 复变函数 一、复变函数的定义 二、映射的概念 三、典型例题 四、小结与思考

复变函数复变函数的定义一、复1.复变函数的定义：设G是一个复数z=x+iv的集合.如果有一个确定的法则存在按这个法则对于集合G中的每一个复数z,就有一个或几个复数w=u+iv与之对应，那末称复变数W是复变数z的函数（简称复变函数),记作 w=f(z)U

2 一、复变函数的定义 ), ( ). , ( , , , . w f z w z z w u iv G G z x iy = = + = + 复变函数 记 作 之对应 那末称复变数 是复变数 的函数 简 称 每一个复数 就有一个或几个复数 与 个确定的法则存在 按这个法则 对于集合 中 的 设 是一个复数 的集合 如果有一 1.复变函数的定义:

复变函数2.单(多)值函数的定义：如果z的一个值对应着一个W的值.那未我们称函数f(z)是单值的如果z的一个值对应着两个或两个以上W的值,那末我们称函数f(z)是多值的3.定义集合和函数值集合：集合G称为f(z)的定义集合(定义域);对应于G中所有z的一切w值所成的集合G*称为函数值集合u

3 2.单(多)值函数的定义: ( ) . , 我们称函数 是单值的 如 果 的一个值对应着一个 的 值 那 末 f z z w , ( ) . 的 值 那末我们称函数 是多值的 如 果 的一个值对应着两个或两个以上 w f z z 3.定义集合和函数值集合: 集合G 称为 f (z)的定义集合(定义域); . * , 称为函数值集合 对应于G中所有z的一切w 值所成的集合G

复变函数4.复变函数与自变量之间的关系：复变函数w与自变量z之间的关系w=f(z)相当于两个关系式：u=u(x,y),， V=V(x,y)它们确定了自变量为x和v的两个二元实变函数例如，函数w=z，令z=x+iy，w=u+iv,则 u+iv =(x +iy)=x2 - y2 + 2xyi于是函数W=z2对应于两个二元实变函数：u= x? - y2, v= 2xy.1

4 4. 复变函数与自变量之间的关系: : ( ) 相当于两个关系式 复变函数 w 与自变量 z 之间的关系 w = f z u = u(x, y), v = v(x, y), 它们确定了自变量为x 和 y的两个二元实变函数. 例如, , 2 函数w = z 令 z = x + iy, w = u + iv, 2 则 u + iv = (x + iy) 2 , 2 2 = x − y + xyi : 于是函数 w = z 2 对应于两个二元实变函数 , 2 2 u = x − y v = 2xy

复变函数二、映射的概念1.引入：对于复变函数,由于它反映了两对变量u,V和x,V之间的对应关系,因而无法用同一平面内的几何图形表示出来，必须看成是两个复平面上的点集之间的对应关系U

5 二、映射的概念 1. 引入: . , , , , , 的点集之间的对应关系 的几何图形表示出来 必须看成是两个复平面上 和 之间的对应关系 因而无法用同一平面内 对于复变函数 由于它反映了两对变量 x y u v

复变函数2.映射的定义：如果用Z平面上的点表示自变量的值而用另一个平面w平面上的点表示函数w的值，那末函数w=f(z）在几何上就可以看作是把z平面上的一个点集G（定义集合）变到W平面上的一个点集G*（函数值集合）的映射(或变换)。U

6 2.映射的定义: ( ). * ( ) ( ) , ( ) , 或变换 平面上的一个点集 函数值集合 的映射 是 把 平面上的一个点集 定义集合 变 到 值 那末函数 在几何上就可以看作 而用另一个平面 平面上的点表示函数 的 如果用 平面上的点表示自变量 的 值 w G z G w f z w w z z =

复变函数这个映射通常简称为由函数w= f(z)所构成的映射如果G中的点z被映射w= f(z)映射成G*中的点w,那末w称为z的象(映象),而z称为w的原象U

7 . , ( ), ( ) * 的原象 中的点 那 末 称 为 的 象 映 象 而 称 为 如 果 中的点 被映射 映射成 w w z z w G z w = f z G . ( ) 所构成的映射 这个映射通常简称为由函 数 w = f z

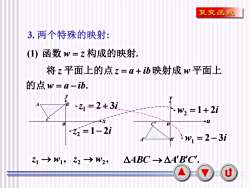
复变函数3.两个特殊的映射：(1)函数W=z构成的映射将z平面上的点z=a+映射成w平面上的点w=a-ib.YB-=2+3i.w2 =1+2i4x+u =1-2i!Wi =2-3i△ABC-AA'B'C'Zi →W1,Z2 →W2,U

8 (1) 函数 w = z 构成的映射. x y o u v o z 2 3i  1 = + w 2 3i  1 = − z 1 2i  2 = − w 1 2i  2 = + A B C A B C , 1 w1 z → , 2 w2 z → ABC → ABC . 3. 两个特殊的映射: . w a ib z z a ib w = − = + 的点 将 平面上的点 映射成 平面上

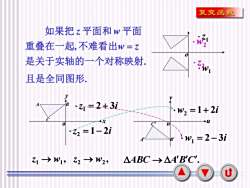
复变函数如果把z平面和w平面重叠在一起，不难看出W=z是关于实轴的一个对称映射且是全同图形YB-=2±3iw2 =1+2iIx+u z =1-2iW=2-3i△ABC -AA'B'C'Zi → W1, Z2 →W2'U

9 x y o u v o z 2 3i  1 = + w 2 3i  1 = − z 1 2i  2 = − w 1 2i  2 = + A B C A B C , 1 w1 z → , 2 w2 z → ABC → ABC . . , 是关于实轴的一个对称映射 重叠在一起 不难看出 如果把 平面和 平面 w z z w = o w1  w2  1 z 2 z 且是全同图形

复变函数(2)函数 w =z2构成的映射.显然将z平面上的点 z=i, =1+2i, =—1映射成w平面上的点w =-1,w2 =-3+4i,Ws=1.V.W215Z.1+x+u0Z3W1-w3U

10 (2) . 函数 w = z 2 构成的映射 1, 3 4 , 1. , 1 2 , 1 1 2 3 1 2 3 = − = − + = = = + = − w w w i w z z i z i z 映射成 平面上的点 显然将 平面上的点 x y o u v o  1 z  2 z w2    w3 3 w1 z