《复变函数与积分变换》课程教学资源（PPT课件）第四章 解析函数的级数表示 4.0 习题课

复变函数第四章级数一、重点与难点二、 内容提要三、典型例题U

复变函数一、重点与难点重点：函数展开成泰勒级数与洛朗级数难点：函数展开成洛朗级数

2 一、重点与难点 重点： 难点： 函数展开成泰勒级数与洛朗级数 函数展开成洛朗级数

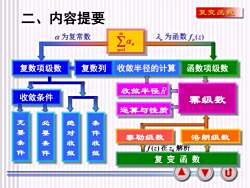
复变函数二、内容提要00α为复常数a,为函数 f,(z)Za复数列复数项级数收敛半径的计算函数项级数收敛半径R收敛条件幂级数运算与性质充要条件必要条件绝对收敛条件收敛泰勒级数洛朗级数f()在Z解析复变函数山

3 复数项级数 函数项级数 充 要 条 件 必 要 条 件 幂级数 收敛半径R 复 变 函 数 绝 对 收 敛 运算与性质 f (z) 在 z0 解析  为复常数 f (z) n 为函数 n   n=1  n 收敛条件 条 件 收 敛 复数列 收敛半径的计算 泰勒级数 洛朗级数 二、内容提要

复变函数1.复数列设{α}(n=1,2,)为一复数列其中αn=an+ibn，又设α=a+ib为一确定的复数如果任意给定ε>0,相应地都能找到一个正数N(),使αn-αN时成立,那末α称为复数列iα,当n→8时的极限记作limαn =α.n->00此时也称复数列α，收敛于αu

4 1.复数列 如果任意给定  0,相应地都能找到一个正数 N( ),使 在n N 时成立,  n −    那末 称为复数列{ }当n → 时的极限,  n 记作 lim = . → n n 此时也称复数列{ }收敛于. n 设{ } (n = 1,2, )为一复数列,其中 n , n n n  = a + ib 又设 = a + ib为一确定的复数

复变函数2.复数项级数1)定义设(αn} ={an+bn}(n=1,2,.)为一复数列8Z表达式αu=α,+α,+..+αn +..Rnn=1称为复数项无穷级数部分和其最前面 n项的和sn=α +αz++α,称为级数的部分和u

5  = + ++ +  = n n n 1 2  1 表达式 称为复数项无穷级数. 其最前面 n 项的和 n n s = 1 + 2 ++ 称为级数的部分和. 部分和 2.复数项级数 设{ } = {a + b }(n = 1,2, )为一复数列, 1) 定义 n n n

复变函数2)复级数的收敛与发散8Zα,收敛，，那末级数如果部分和数列s,收敛，n=1并且极限lims,=s称为级数的和n-0080Zα,发散如果部分和数列s,不收敛，那末级数n=1888Za,与α,收敛台b,都收敛充要条件118Wn=1n=l必要条件α,收敛=limα,= 0n0n=lu

6 2) 复级数的收敛与发散 lim 0 1  = →  =  n n n  n收敛   收敛  与 都收敛  =  =  =  1 1 n 1 n n n 充要条件  n an b 必要条件 如果部分和数列{ }收敛, n s , 1 那末级数 收敛  n= n 并且极限lim s s 称为级数的和. n n = → 如果部分和数列{ }不收敛, n s . 1 那末级数 发散  n= n

复变函数3)复级数的绝对收敛与条件收敛808Z如果αn为绝对收敛α，收敛，那末称级数n=1n=1非绝对收敛的收敛级数称为条件收敛级数8088ZZa,与b,绝对收敛.α,绝对收敛个n=1n=1n=1绝对收敛一一条件收敛u

7 非绝对收敛的收敛级数称为条件收敛级数. 3)复级数的绝对收敛与条件收敛 如果  收敛, 那末称级数 为绝对收敛.  n=1  n   n=1  n . 1 1 1  绝对收敛  与 绝对收敛  =  =  =  n n n n n n a b 绝对收敛 条件收敛

复变函数3.复变函数项级数设({f,(z)(n =1,2,)为一复变函数序列其中各项在区域D内有定义.表达式00E f.(z) = fi(z)+ f(z)+.+ f.(z)+ ..n=18Zf,(z).称为复变函数项级数，记作n=1级数最前面n项的和Sn(z) = fi(z)+ f2(z)+...+ fn(z)称为这级数的部分和u

8 ( ) ( ) ( ) ( ) 1 2 s z f z f z f z n = + ++ n 称为这级数的部分和. 级数最前面 n 项的和 3.复变函数项级数 设{ f (z)}(n = 1,2, )为一复变函数序列, n  = + ++ +  = ( ) ( ) ( ) ( ) 1 2 1 f z f z f z f z n n n 其中各项在区域 D内有定义.表达式 称为复变函数项级数, 记作 ( ). 1   n= n f z

复变函数4.幂级数1)在复变函数项级数中,形如8Zc,(z-a)"=Co +c(z-a)+c(z-a) +.n=0+c,(z -a)" +...的级数称为幂级数当a=0时,8Z"=o ++++n".n=1u

9 4. 幂级数 1) 在复变函数项级数中, 形如 c z c c z c z c z . n n n n  n = + + ++ +  = 2 0 1 2 1 的级数称为幂级数. 当a = 0时,  − = + − + − +  = 2 0 1 2 0 c (z a) c c (z a) c (z a) n n n + cn (z − a) n +

复变函数2)收敛定理---阿贝尔Abel定理8c,z"在 z=Zo(± 0)收敛,那末对如果级数n=0满足o的z，级数必发散u

10 -阿贝尔Abel定理 如果级数   n=0 n n c z ( 0) z = z0  0 z  z 0 z = z 0 z  z z, 在 收敛, z, 那末对 的 级数必绝对收敛, 如果在 级数发散, 那末对满足 的 级数必发散. 满足 2)收敛定理