《复变函数与积分变换》课程教学资源（PPT课件）第九章 拉普拉斯变换（Laplace变换）

复变函数第九章Laplace变换U

第九章 Laplace变换

复变函数Fourier变换的两个限制：(1)定义于[0,+0),而不必考虑t<0时取值的函数(2)绝对可积的条件太强。许多简单函数的傅氏变换或者不存在，或者为非常义下的广义函数给应用带来很大的不方便

2 (1) [0 ), 0 (2) 定义于 ，+   而不必考虑t 时取值的函数； 绝对可积的条件太强。许多简单函数的傅氏 变换或者不存在，或者为非常义下的广义函 数给应用带来很大的不方便。 Fourier变换的两个限制：

s1Laplace变换的概念复变函数[0,t 0)e-Brt≥0考虑f(t) t E(-0,+o0),有f(t)u(t)=f(t) t≥0.若存在β>0,使 lime-Bif(t)=0,则/e-βtf(t) dt 80那磨f(t)u(t)e-βB的傅氏积分总是存在的。F[f(t)u(t)e-B ] = (t f(t)u(t)e-Bte-jot dtS+* f(t)e-(β+jo) dt S=β+ jo f f(t)e-s dtAF(s)U

3 §1 Laplace变换的概念 0, 0 ( ) ( 0). , 0 t t t e t    −   =     设指数衰减函数 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) , 0. 0, lim . t t t t f t t f t u t f t t e f t e f t dt f t u t e      − − →  −  − +    +  + - 考虑 ,有 = 若存在 使 =0,则 那麽 的傅氏积分总是存在的。 ( ) ( ) 0 0 [ ( ) ( ) ] ( ) ( ) ( ) ( ) t t j t j t st f t u t e f t u t e e dt f t e dt s j f t e dt F s        + − − − − + + − + − = = = +     F

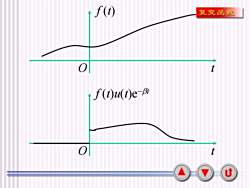
f(t)复变函数0f(t)u(t)e-βt01U

4 t f (t) O t f (t)u(t)e−t O

复变函数1.定义：设,f(t)是[0,+o0)上的实(或复)值函数，若对参数s=β+ jO,F(s)=dof(t)e-sdt在s平面的某一区域内收敛，则称其为,f(t)的Laplace变换，记为L[f(t)] = F(s) = (e f(t)e-st dtf(t)称为F(s)的Laplace逆变换，记为f(t)= L'[F(s))F(s)称为像函数，f(t)称为原像函数u

5 ( ) 0 0 1 ( ) [0, ) ( ) , ( ) ( ) ( ) Laplace [ ( )] ( ) ( ) ( ) Laplace ( ) [ ( )]. ( ) ( ) st st f t s j F s f t e dt f t f t F s f t e dt f t F s f t F s F s f t   + − + − − + = + = = = =   设 是 上的实 或复 值函数，若对参数 在s平面的某一区域 内收敛，则称其为 的 变换，记为 称为 的 逆变换，记为 称为像函数， 称为原像函数. L L 1. 定义：

0t0数·根据拉氏变换的定义，有这个积分在)=d时收毁,而且有+81+8-ste-stdt =-e二JosS101所以 L[u(t)](Re(s) > 0)Su

6 例1 求单位阶跃函 数 0 0 ( ) 1 0 t u t t   =    的拉氏变换. 0 [ ( )] e dst u t t + − =  L • 根据拉氏变换的定义, 有 这个积分在Re(s)>0时收敛, 而且有 0 1 1 e d e 0 st st t s s + − − + = − =  1 [ ( )] (Re( ) 0). u t s s 所以 L = 

例2求指数函数,f()=e kt的拉氏变换(k为实数).根据拉氏变换的定义，有-Oe-(s-k)tdtC[f(t)]= Teae-stdt=0。这个积分在Re(s)>k时收敛,而且有1180e-(s-k)tf0 e-(s-k)tdt=s-ks-k所以 L[ek]=(Re(s) >k)S-k其实为复数时上式也成立，只是收敛区间为uRe(s)>Re(k)

7 例2 求指数函数 f (t)=e kt 的拉氏变换(k 为实数). ( ) 0 0 [ ( )] e e d e d kt st s k t f t t t + + − − − = =   L ( ) ( ) 0 0 1 1 e d e s k t s k t t s k s k + + − − − − = − = − −  • 这个积分在Re(s)>k时收敛, 而且有 其实k为复数时上式也成立, 只是收敛区间为 Re(s)>Re(k) 1 [e ] (Re( ) ). kt s k s k =  − 所以 L 根据拉氏变换的定义, 有

(1）在t≥0的任一有限区间上分段连续;(2）当t>+8时,f(t)的增长速度不超过某一指数函数,即存在常数M>0及c≥0.使得If (t)|≤ M e ct, 0≤ t c上一定存在,并且在Re(s)> c的半平面内,F(s)为解析函数u

8 2.拉氏变换的存在定理 若函数f (t)满足: (1) 在t  0的任一有限区间上分段连续; (2) 当t→+时, f (t)的增长速度不超过某 一指数函数, 即存在常数 M > 0及c  0, 使得 |f (t)| M e ct, 0 t c上一定存在, 并且在Re(s) > c的半平 面内, F(s)为解析函数

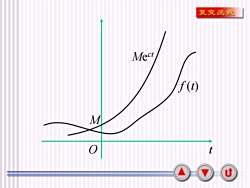
复变函数Mectf(t)M0U

9 M Me ct f (t) O t

(0≤t0(即β≥C+=所以[("ed=MC注l:大部分常用函数(a变换都存在(常义下)注2：存在定理的条件是充分但非必要条件u

10 说明：由条件2可知, 对于任何t值 (0t0 (即  c+e = c1>c), 则 | f (t)e−st|  Me −et . 0 0 ( )e d e d . st t M f t t M t e e + + − −  =   所以 注1:大部分常用函数的Laplace变换都存在(常义下); 注2：存在定理的条件是充分但非必要条件