《高等数学》课程教学资源（PPT课件）第十二章 无穷级数 12-02 第二节 常数项级数的审敛法

第二节常数项级数的审敛法■正项级数及其审敛法1交错级数及其审敛法1绝对收敛与条件收敛小结思考题

◼ 正项级数及其审敛法 ◼ 交错级数及其审敛法 ◼ 绝对收敛与条件收敛 ◼ 小结 思考题 第二节 常数项级数的审敛法

正项级数及其审敛法positive term series8Zu,≥0正项级数1.定义un=12.收敛的充要条件SiS,..MSn...单调增加数列这时.只可能有两种情形：正项级数及其审敛法80(1)当n→o时, Sn→+o0. 级数u.必发散n=1(2)若(s,}有上界,即s,≤u(正常数)台lim s, = sn→8

1. 定义   n=1 un 正项级数 s1  s2  sn  2. 收敛的充要条件 单调增加数列 这时,只可能有两种情形: → +. n s s s n n = →  lim (1)当n→时, . 1 级 数 必发散  n= un (2) 若{ }有上界, n s 即  (正常数) n s positive term series 正 项 级 数 及 其 审 敛 法 un  0 一、正项级数及其审敛法

定理1（基本定理）部分和所成的数列s,有界正项级数收敛台(sn≤s≤u)注正项级数可以任意加括号,其敛散性不变对收敛的正项级数,其和也不变正项级数及其审敛法

定理1(基本定理) (s  s  ) n 注 正项级数可以任意加括号,其敛散性不变, 对收敛的正项级数,其和也不变. 正 项 级 数 及 其 审 敛 法 正项级数收敛  部分和所成的数列 n s 有界

正项级数收敛台部分和所成的数列s,有界802例判定的敛散性,2h+n=l由于解故级数的部分和2" + 111S.22 +122″+111<1222"2T正项级数及其审敛法由定理1知，该正项级数收敛这个例启示我们：判定一个正项级数的敛散性可与另一个已知敛散性的正项级数比较来确定

例 判定  的敛散性.  =1 2 + 1 1 n n 解 2 1 1 + n 2 1 1 2 1 1 2 1 1 2 + + + + + + = n n S  n 2 1 2 1 2 1 2  + ++ n 2 1 = 1− 由定理1知, 故级数的部分和 可与另一个已知敛散性的正项级数比较来确定. 正 项 级 数 及 其 审 敛 法 , 2 1 n   1 该正项级数收敛. 这个例启示我们:判定一个正项级数的敛散性, 由于 正项级数收敛  部分和所成的数列 n s 有界

3.比较审敛法则定理2 若0≤un≤vn，88ZZ收敛收敛VWnn=ln=188ZZuvn发散发散二In=1n=18证 设=<vVU1n正项级数及其审敛法n=1且/snu +u, +...+un ≤yi+v? +..+vsKg8Zu,收敛即部分和数列有界，n=1

3. 比较审敛法 证 定理2 n u u un 且s = 1 + 2 ++   = = n 1 n 设 v n n u  v   即部分和数列有界.   =  n 1 un n  v + v ++ v 1 2 正 项 级 数 及 其 审 敛 法 , n n 若 u  v 则   n=1 n v 收敛    n=1 un 收敛   n=1 un 发散    n=1 n v 发散 收敛 0 

808ZZun发散二vn发散若0≤u,≤vnn:n=1n=l证 设s,→(n→8)且un≤vn则a,≥Sn→80不是有界数列8v，发散定理证毕n=18若u,收敛(发散)推论1) 且vn≤ku,(n>N)n=1正项级数及其审敛法8(kun≤vn）则y,收敛(发散)n=1比较审敛法的不便：须有参考级数

n n 则  s s →  (n → ) 设 n n n 且 u  v →  不是有界数列   =  n 1 n v 定理证毕. 比较审敛法的不便:须有参考级数. 正 项 级 数 及 其 审 敛 法   n=1 un 发散    n=1 n v 发散 发散 推论1   n=1 若 un 收敛(发散) v ku (n N ) 且 n  n  ( ) n n ku  v   n=1 n 则 v 收敛(发散) 证 0 , n n 若  u  v

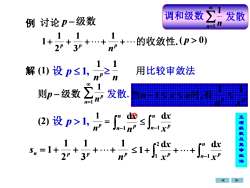
81Z发散调和级数例讨论p-级数nn=1的收敛性.(p>0)7解(1)设p≤1,用比较审敛法10n21发散.则p-级数当时有hpn=1dxdrenn正项级数及其审敛法(2) 设p>1,111SY2p3P

解 设 p  1, 则p −级数 设 p  1, = p n 1 n p p p n s 1 3 1 2 1 = 1+ + ++   −  + + + n n p p x x x x 1 2 1 d d 1  (1) (2) 正 项 级 数 及 其 审 敛 法   =1 1 n n 调和级数 发散 n n p 1 1   −  n n p x x 1 d 用比较审敛法  发散.  =1 1 n p n p p n x n x n 1 1 当 − 1   时,有   − n n p n x 1 d 例 讨论 p −级数 + p + p ++ p + n 1 3 1 2 1 1 的收敛性. ( p  0)

7即s,有界,则p-级数>收敛.(p>1)正项级数及其审敛法n=1h或(2)设p>1,将p-级数加括号如下：248ΛΛ15它的各项均不大于下述正项级数的对应项

 = + n p x dx 1 1 ) 1 (1 1 1 1 −1 − − = + p p n 1 1 1 −  + p 即 有界, n s 或(2) 设 p  1, 将p-级数加括号如下:   +       + + +       + + + +      + + p p p p p p p p 15 1 8 1 7 1 6 1 5 1 4 1 3 1 2 1 1 2 4 8 ^ ^ ^ 它的各项均不大于下述正项级数的对应项   +       + + +       + + + +      + + p p p p p p p p 8 1 8 1 4 1 4 1 4 1 4 1 2 1 2 1 1 正 项 级 数 及 其 审 敛 法 n s 则p −级数 收敛.  =1 1 n p n ( p  1)

2六2p-1力11这是收敛的等比级数，公比2 p-181故由比较判别法知p>1时,p--级数收敛.正项级数及其审敛法hpn=l收敛当p>1时,p-级数发散当p≤1时

= + −1 + −1 + −1 + 8 1 4 1 2 1 1 p p p  +       +      = + + − − − 3 1 2 1 1 2 1 2 1 2 1 1 p p p 这是收敛的等比级数, 1. 2 1 1 =  p− q 故由比较判别法知 p>1时, p-级数   =1 1 n p n      − 当 时 发 散 当 时 收 敛 级 数 1 , 1 , p p p 正 项 级 数 及 其 审 敛 法 公比 收敛

使用正项级数的比较判定法时，需要知道一些级数的敛散性，作为比较的标准常用的比较级数当q1时，收敛Z(2) p-级数正项级数及其审敛法当p≤1时，发散nn=18人发散(3) 调和级数hn=1

(1) 几何级数 使用正项级数的比较判定法时, 常用的比较级数 正 项 级 数 及 其 审 敛 法 一些级数的敛散性,作为比较的标准. 需要知道 (2) p-级数 (3) 调和级数         = 当 时 发 散 当 时 收 敛 1 , 1 , 0 q q aq n n      当 时 发散 当 时 收敛 1 , 1 , p p   =1 1 n p n  = + + ++ +  n= n n 1 3 1 2 1 1 1 1 发散