《高等数学》课程教学资源（PPT课件）第十一章 曲线曲面积分 11-07 第七节 斯托克斯公式、环流量与旋度

第七节斯托克斯公式环流量与旋度■斯托克斯公式简单应用环流量与旋度■小结思考题

环流量与旋度 第七节 斯托克斯公式 ◼ 斯托克斯公式 ◼ 简单应用 ◼ 环流量与旋度 ◼ 小结 思考题

斯托克斯（Stokes）公式，Z的定理1设光滑曲面的边界I是分段光滑曲线，P,Q,R 在包含E在内侧与I的正向符合右手法则的一个空间域内具有连续则有一阶偏导数，aQapaRapaRaQIydz+dzdx+dxdiOz0xoyayOzaxZnΦ Pdx+Qdy+RdzZT（斯托克斯公式）X

一、 斯托克斯( Stokes ) 公式 定理1 设光滑曲面的边界是分段光滑曲线, d d d P x Q y R z  = + +  (斯托克斯公式) 的一个空间域内具有连续一阶偏导数, 的 侧与的正向符合右手法则, 在包含在内   y o z x n Dx y C 则有

证情形1Z与平行z轴的直线只交于nZ一点，设其方程为E:z= f(x,y), (x,y)eDx为确定起见，不妨设取上侧（如图)）则 $_ Pdx=Φ_P(x,y,z(x,y)dx（利用格林公式）a-11P(x,y,z(x,y)dxd yDay

证 情形1 与平行z轴的直线只交于 一点, 设其方程为 : ( , ), ( , ) xy  =  z f x y x y D 为确定起见, 不妨设取上侧 (如图).   y o z x n Dx y C 则 P x d   ( , , ( , ))d C = P x y z x y x  (利用格林公式) ( , , ( , ))d d Dxy P x y z x y x y y  = −  

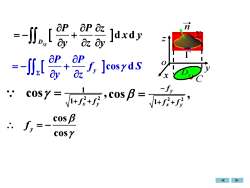
napap oz-,m[dxdyayOz Qy2apap=-[,[J, Jcos ydsayzX1co=i+f+f,cos β=1+f?+.cosβf,=-cos

 d d Dxy P P z x y y z y    = − +      y cos d P P f S y z     = − +    2 2 1 1 cos , x y f f  + + = 2 2 1 cos , y x y f f f  − + + = cos cos y f    = −   y o z x n Dx y C

apaP cosβ因此§, Pdx=-],[cosyd sayOz cosapapS,[cosy Jdscos pOzayapapS]dzddxdy>Oz.ayaqaq同理可证$,Qdy= J],dydzaxazaRaRf_ Rdx=IdzdxdV(MaxQy三式相加，即得斯托克斯公式：

因此   cos d cos d cos P P P x S y z        = − −      cos cos d P P S z y      = −    d d d d P P z x x y z y    = −    同理可证 Q y d   d d d d Q Q x y y z x z    = −    R x d   d d d d R R y z z x  y x   = −    三式相加,即得斯托克斯公式;

情形2 曲面Z与平行z轴的直线交点多于一个，则可通过作辅助线面把分成与轴只交于一点的几部分在每一部分上应用斯托克斯公式,然后相加，由于沿辅助曲线方向相反的两个曲线积分相加刚好抵消证毕所以对这类曲面斯托克斯公式仍成立注意如果是xoy面上的一块平面区域则斯托克斯公式就是格林公式故格林公式是斯托克斯公式的特例

情形2 曲面与平行z轴的直线交点多于一个, 则可 通过作辅助线面把分成与z轴只交于一点的几部分, 在每一部分上应用斯托克斯公式,然后相加, 由于 沿辅助曲线方向相反的两个曲线积分相加刚好抵消, 所以对这 类曲面斯托克斯公式仍成立. 注意 如果是xoy面上的一块平面区域, 则斯托克斯 公式就是格林公式, 故格林公式是斯托克斯公式的特例. 证毕

为便于记忆,斯托克斯公式还可写作：dydz dzdx dxdyaaaJP_Pdx+Qdy+RdzaxOz.oy2PRQ或用第一类曲面积分表示：cos βcosαcos aaaJdS =Φ,Pdx+Qdy+RdzOz.ax2QPR

为便于记忆,斯托克斯公式还可写作: d d d d d d y z z x x y x y z P Q R         d d d P x Q y R z  = + +  或用第一类曲面积分表示: cos cos cos d S xyz P Q R            d d d P x Q y R z  = + + 

Stokes公式的实质：表达了有向曲面上的曲面积分与其边界曲线上的曲线积分之间的关系（当Z是xoy面的平面闭区域时）特殊情形格林公式斯托克斯公式二、 简单的应用

Stokes公式的实质: 表达了有向曲面上的曲面积分与其边界曲线上 的曲线积分之间的关系. 斯托克斯公式 特殊情形 格林公式 (当 Σ 是xoy面的平面闭区域时) 二、简单的应用

zdx+xdy+ydz例1利用斯托克斯公式计算积分其中r为平面x+y+z=1被三坐标面所截三角形的整个边界,方向如图所示分析记三角形域为Z,取上侧，直接利用斯托克斯公式解Φ.zdx+xdy+ydzdzdxdydzdxdyxyaaaJazaxay利用轮换对称性xyZ3dydz+dzdx+dxdy =3 JJdxdy=-2Dxy

d d d d d d x y z y z z x x y z x y        =  z x y 1 1 1 o 例1 利用斯托克斯公式计算积分 其中为平面x+y+z=1被三坐标面所截三角形的整个 分析 记三角形域为, 取上侧，直接利用 斯托克斯公式. 解 边界, 方向如图所示. d d d d d d y z z x x y  = + +  利用轮换对称性 3 d d Dx y = x y  3 2 = Dxy

例2计算曲线积分f(y2 -z)dx+(z? -x")dy+(x? - )dz3截立方体:0≤x≤1,其中I是平面x+y+z=-20≤y≤1,0≤z≤1的表面所得的截痕,若从 0X轴的正向看去,取逆时针方向。n23分析取为平面x+y+z=E2的上侧被I所围成的部分1则 n=[1,1,1]

例 2 计算曲线积分 ( y z )dx (z x )dy (x y )dz 2 2 2 2 2 2 − + − + −  其中是平面 2 3 x + y + z = 截立方体:0  x  1, 0  y  1,0  z  1的表面所得的截痕,若从 ox 轴的正向看去,取逆时针方向. 分析 取 Σ 为平面 2 3 x + y + z = 的上侧被所围成的部分. 则 {1,1,1} 3 1 n =  z x y o  n  