《高等数学》课程教学资源（PPT课件）第九章 多元函数微分法及其应用 9-习题课

第九章多元函数微分法及其应用习题课>教学要求>典型例题

第九章 多元函数微分法及其应用 习习 题题 课课 ➢教学要求 ➢典型例题

教学要求一、1.理解多元函数的概念，2.了解二元函数极限与连续概念，掌握有界闭区域上二元连续函数的性质、全微分存在的必要条件与充分条件．了解二元函数极限、连续、存在偏导与可微之间的关系。3.熟练掌握偏导数的定义与求法，特别要掌握复合函数与隐函数偏导数的求法.会求函数的全微分

一、教学要求 1.理解多元函数的概念. 存在偏导与可微之间的关系. 掌握复合函数与隐函数偏导数的求法. 2.了解二元函数极限与连续概念, 掌握有界 闭区域上二元连续函数的性质、全微分存在的 必要条件与充分条件. 了解二元函数极限、 3.熟练掌握偏导数的定义与求法, 特别要 会求函 数的全微分. 连续

4.熟练掌握空间曲线的切线与法平面方程、曲面的切平面与法线方程的求法5.熟练掌握二元函数的极值理论及其求法，会用拉格朗日乘数法求多元函数的极值以及有关应用题6.了解方向导数与梯度的概念及其计算方法

6.了解方向导数与梯度的概念及其计 会用拉格朗日乘数法求多元函数的 4.熟练掌握空间曲线的切线与法平面 方程、曲面的切平面与法线方程的求法. 5.熟练掌握二元函数的极值理论及其 求法, 极值以及有关应用题. 算方法

二、典型例题例1 设z=x2f(xy,),(f 具有二阶连续偏导数a2zOz az求ay'ay2' axay-3(fix + f"-)= x*f"+ x"f解ra"zx* (fix + fi =) +x(fix + fu)ay= x"f1 + 2xf1" + xf22

例1 解 设 3 ( , ), ( f 具有二阶连续偏导数)， x y z = x f xy =   y z 2 2 1 4 = x f + x f  =   2 2 y z 2 , 12 22 3 11 5 = x f  + x f  + xf  2 + x 二、典型例题 , , . 2 2 2 x y z y z y z        求 3 x ( f 1 x ) 1 2 x + f  4 x f x 11 (  ) 1 12 x + f  ( f 21  x ) 1 22 x + f 

α-xf'+xf"z= x'f(xy,二aya~zaa(xf'+xf2)axdyaxayax= 4x3 f' + x'lfiy+ f(--2+2xf+ x"[fy + f(-Y= 4x3 f'+ 2xf2 + x yfl - yf2

=    x y z 2 1 3 = 4x f  ( ) 2 2 1 4 x f x f x +    = 4 2 . 11 22 4 1 2 3 = x f + xf  + x yf  − yf  2 2 1 4 x f x f y z = +    2 + x 4 + x  + 2 2xf ( , ) 3 x y z = x f xy y x z    2 f y 11 [  ( )] 12 2 x y + f  − f y 21 [  ( )] 22 2 x y + f  −

u= f(x,y),例2设函数u(x)由方程组g(x,y,z) = 0.h(x,z) = 0.ahogdu所确定,且#0, 求±0Ozoydx分析变量4个，方程3个独立自变量1个.由题意选x为独立自变量.则u=u(x),y= (x),z= z(x)解 法一方程组各方程两边微分，得du = f,dx + f,dydx + g,dz)gdx + g,dy + g,dz = 0= dy =gyh.dx + h.dz = 0hdx.dz川D

     = = = ( , ) 0. ( , , ) 0, ( , ), ( ) h x z g x y z u f x y 设函数 u x 由方程组 解 例2 法一 方程组各方程两边微分, 得 u f x f y d = xd + yd gxdx + gydy + gzdz = 0 hxdx + hzdz = 0 d dx. h h z z x = − ( d d ) 1 d g x g z g y x z y = − + 分析 变量4个,方程3个, 则u = u(x), y = y(x),z = z(x) , 0,  0,      z h y g 所确定 且 . d d x u 求 独立自变量1个.由题意 选x为独立自变量.  

u= f(x,y),得法二方程组各方程两边对x求导，g(x, y,z)= 0dudy(1)h(x,z)=0.XLdxdxdzdy(2)0gx+gy+gzdxdxdz(3)h0xdxdy_g,·hxhydzgx代入(2)得由(3)得dxg,·hzgydxMS,g,-h.dufy'gx代入(1)得?dxg,-h,gy

= x u d d 由(3)得 代入(2)得 代入(1)得 法二      = = = ( , ) 0. ( , , ) 0, ( , ), h x z g x y z u f x y 方程组各方程两边对x求导, 得         gx hx , d d z x h h x z = − , d d y x y z z x g g g h g h x y −   = . d d y z y z x y y x x g h f g h g f g f x u    +  = − x f x y f y d d + (1) x y gy d d +  x z gz d d +  = 0 (2) x z hz d d +  = 0 (3)

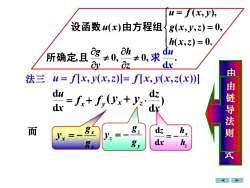
u= f(x,y),设函数u(x)由方程组g(x, y,z) = 0h(x,z) = 0.ahduag#0,求所确定,且±0.az.avdx由日由链导法则法三u= f[x, y(x,z)]= f[x, y(x,z(x)duf+ f,(yx+ y)dxdxg.gx而hdzxVVZX公dxg911式

法三 u = f[x, y(x,z)]= f[x, y(x,z(x))] = x u d d 而 y x x g g y = − y z z g g y = − z x h h x z = − d d y + f z + y      = = = ( , ) 0. ( , , ) 0, ( , ), ( ) h x z g x y z u f x y 设函数 u x 由方程组 , 0,  0,      z h y g 所确定 且 . d d x u 求 x f x ( y ) d d x z 

例3求旋转抛物面z=x2+2与平面x+-2z=2之间的最短距离解 法一拉格朗日乘数法设P(x,y,z)为抛物面z=x2+y2上任一点则P到平面x+y-2z-2=0的距离为d,x+ y-2z-2.本题变为求一点P(x,y,z),使得x,J,z分析满足x2+y2-z=0且使d =x+y-2z-2(即d2:(x+ y-2z-2))最小

2 2 2 2 例3 求旋转抛物面z = x + y 与平面 x + y − z = 解 ( , , ) , 设 P x y z 为抛物面 z = x 2 + y 2 上任一点 分析 本题变为求一点P(x, y,z), 法一 拉格朗日乘数法. 之间的最短距离． 则P 到平面 x + y − 2z − 2 = 0的距离为d, 2 2. 6 1 d = x + y − z − 使得 x, y,z 满足即 ( 2 2) )最小． 6 1 ( 2 2 d = x + y − z − 2 2 6 1 0且 使 d = x + y − z − 2 2 x + y − z =

求旋转抛物面z=x2+y2与平面x+y-2z=2之间的最短距离(即d2=(x+-2z-2))最小.令 L(x,y,z) =(x + -2z-2)+(z-x2 - ),得1(x+y-2z-2)-2ax=0, (1)3(2)(x+y-2z-2)-22y=0, 31(3)x + y - 2z -2)(-2) + z = 0,(4)+y解此方程组得

( 2 2) ( ), 6 1 ( , , ) 2 2 2 令 L x y z = x + y − z − +  z − x − y 解此方程组得 得 . 8 1 , 4 1 , 4 1 x = y = z = 2 2 2 2 求旋转抛物面z = x + y 与平面 x + y − z = 之间的最短距离． ( 2 2) 2 0, (1) 3 1 L x = x + y − z − − x = ( 2 2) 2 0, (2) 3 1 L y = x + y − z − − y = ( 2 2)( 2) 0, (3) 3 1 Lz  = x + y − z − − + z = , (4) 2 2 z = x + y        即 ( 2 2) )最小． 6 1 ( 2 2 d = x + y − z −