《高等数学》课程教学资源（PPT课件）第八章 向量代数与空间解析几何 8-6 第六节 空间曲线及其方程（space curve）

第六节空间曲线及其方程(space curve)1空间曲线的一般方程1空间曲线的参数方程空间曲线在坐标面上的投影作业■小结思考题

第六节 空间曲线及其方程 ◼ 空间曲线的一般方程 ◼ 空间曲线的参数方程 ◼ 空间曲线在坐标面上的投影 ◼ 小结 思考题 作业 (space curve)

空间曲线的一般方程空间曲线C可看作空间两曲面的交线7[F(x,y,z) = 0SS[G(x,y,z) = 0空间曲线的一般方程y特点：曲线上的点都满足方程满足方程的点都在曲线上，不在曲线上的点不能同时满足两个方程

一、空间曲线的一般方程    空间曲线的一般方程 空间曲线C可看作 特点：曲线上的点都满足方程, 满足方程的点都在曲线上, 不在曲线上的点不能 同时满足两个方程. 空间两曲面的交线. x y z O S1 S2 C F(x, y,z) = 0 G(x, y,z) = 0

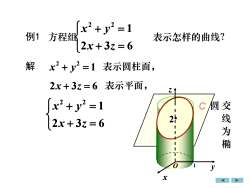
x2=121例1方程组表示怎样的曲线？2x+3z= 6解x2+2=1 表示圆柱面,2x+3z=6表示平面，x? + y2 =1圆交福人线为椭2h2x + 3z = 6-0yx

例1 方程组 表示怎样的曲线？    + = + = 2 3 6 1 2 2 x z x y 解 1 2 2 x + y = 表示圆柱面， 2x + 3z = 6 表示平面，    + = + = 2 3 6 1 2 2 x z x y 交 线 为 椭 C 圆 1 z x O y 2

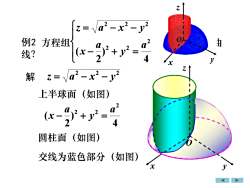
N02O1例2由方程组线?4y7解z=a2-x2-y上半球面 (如图)2N圆柱面 (如图)(如图)交线为蓝色部分1x

例2 方程组 表示怎样的曲 线？      − + = = − − 4 ) 2 ( 2 2 2 2 2 2 a y a x z a x y 解 2 2 2 z = a − x − y 上半球面（如图） 4 ) 2 ( 2 2 2 a y a x − + = 圆柱面（如图） 交线为蓝色部分（如图） z x y O x y z O

二、空间曲线的参数方程x = x(t)空间曲线的参数方程y= y(t)z = z(t)当给定t=t,时，就得到曲线上的一个点(xi,Ji,z),随着参数的变化可得到曲线上的全部点

二、空间曲线的参数方程      = = = ( ) ( ) ( ) z z t y y t x x t 空间曲线的参数方程 随着参数的变化可得到曲线上的 , 当给定t = t 1时 就得到曲线上的一个点 ( , , ), 1 1 1 x y z 全部点

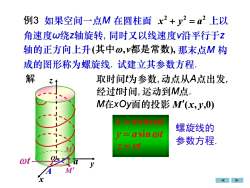
例3x2+y?=α2 上以如果空间一点M在圆柱面角速度w绕z轴旋转，同时又以线速度v沿平行于z轴的正方向上升(其中の,v都是常数),那末点M 构试建立其参数方程成的图形称为螺旋线解取时间为参数，动点从A点出发Z经过时间，运动到M点M在xOy面的投影M(x,y,0)x=acosot螺旋线的y=asint参数方程z =vtotyM1X

动点从A点出发, x = acost y = asint z = vt 螺旋线的 参数方程. 解 取时间t为参数, 经过t时间, 运动到M点. 例3 (其中,v都是常数), 那末点M 构 成的图形称为螺旋线. 试建立其参数方程. M在xOy面的投影 M(x, y,0) z x y O •M M • A • t a 轴的正方向上升 如果空间一点M 在圆柱面 2 2 2 x + y = a 上以 角速度ω绕z轴旋转, 同时又以线速度v沿平行于z

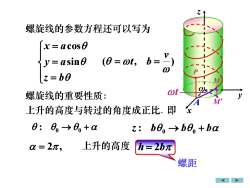
z螺旋线的参数方程还可以写为x=acosa(O = wt, b =y=asine0z=boot螺旋线的重要性质：yM4上升的高度与转过的角度成正比．即x: → +αz: b0→b0.+bo上升的高度α=2元,h=2b元螺距

螺旋线的参数方程还可以写为      = = =    z b y a x a sin cos ( , )    v = t b = 螺旋线的重要性质：  :  0 → 0 + z: b 0 → b 0 + b 上升的高度与转过的角度成正比. 即  = 2 , 上升的高度 h = 2b 螺距 z x y O •M M • A • t •P

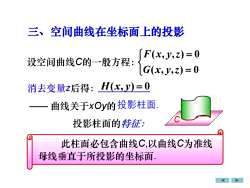
三、空间曲线在坐标面上的投影F(x,y,z) = 0设空间曲线C的一般方程：G(x, y,z) = 0消去变量z后得：H(x,y)=0一曲线关于xOy的投影柱面投影柱面的特征：此柱面必包含曲线C,以曲线C为准线母线垂直于所投影的坐标面

三、空间曲线在坐标面上的投影    = = ( , , ) 0 ( , , ) 0 G x y z F x y z 消去变量z后得： H(x, y) = 0 曲线关于xOy的 设空间曲线C的一般方程： 投影柱面的特征： 此柱面必包含曲线C,以曲线C为准线 、 C 投影柱面. 母线垂直于所投影的坐标面

空间曲线在xOy面上的投影曲线(或称投影)(即为投影柱面与xOy面的交线)H(x,y)=0(即为曲线关于xOy面的投影柱面z=0(即为xOy面)类似地：可定义空间曲线在其它坐标面上的投影xOz面上的投影曲线yOz面上的投影曲线R(y,z) = 0T(x,z)= 0x=0y=0

类似地:可定义空间曲线在其它坐标 面上的投影.    = = 0 ( , ) 0 x R y z    = = 0 ( , ) 0 y T x z yOz面上的投影曲线 xOz面上的投影曲线    = = 0 ( , ) 0 z H x y 空间曲线在xOy 面上的投影曲线(或称投影) (即为曲线关于xOy面的投影柱面) (即为xOy 面) C (即为投影柱面与xOy 面的交线)

x2 +y? +z2 =1例4求曲线在坐标面上的投1Z =影.23xOy面的解（1)消去变量z后得x24投影柱面34在xOy面上的投影为z=01上(2)因为曲线在平面z所以在xOz面上=21的投影为线段/37 =Ix<22y= 0

例4 求曲线 在坐标面上的投 影.      = + + = 2 1 1 2 2 2 z x y z 解 (1) 消去变量z后得 4 2 2 3 x + y = 在 xOy面上的投影为      = + = 0 4 2 2 3 z x y (2) 因为曲线在平面 2 1 z = xOy面的 投影柱面 上 ， 所以在 xOz面上 的投影为线段. 2 3 | | 0 2 1       = = x y z