《高等数学》课程教学资源（PPT课件）第六章 定积分的应用 6-1 第一节 定积分的元素法

第一节定积分的元素法、问题的提出思考题二、 小结

第一节 定积分的元素法 一、问题的提出 二、小结 思考题 1

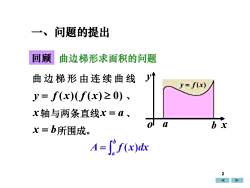
问题的提出、回顾曲边梯形求面积的问题yt曲边梯形由连续曲线y= f(x)y= f(x)(f(x)≥0) ~x轴与两条直线x=a、01ab xx=b所围成。A = f'f(x)dx2

回顾 曲边梯形求面积的问题  = b a A f (x)dx 一、问题的提出 曲 边 梯 形 由 连 续 曲 线 y = f (x)( f ( x)  0) 、 x轴与两条直线x = a 、 x = b所围成。 a b x y o y = f (x) 2

面积表示为定积分的步骤如下（1）把区间[a,bl分成n个长度为△x,的小区间相应的曲边梯形被分为n个小窄曲边梯形，第i个小窄曲边梯形的面积为△A，则A=△A,i=1（2）计算△A,的近似值A, ~ f(5)Ax5; EAx;(3）求和，得A的近似值 A~f(5)Ax;i13

面积表示为定积分的步骤如下 （1）把区间[a,b]分成n个长度为xi 的小区间， 相应的曲边梯形被分为n个小窄曲边梯形，第i 个小窄曲边梯形的面积为Ai，则  = =  n i A Ai 1 . （2）计算Ai 的近似值 i i xi A  f ( )  i xi （3） 求和，得A的近似值 ( ) . 1 i i n i A   f x =  3

（4）求极限，得A的精确值面积元素nA = limZ f(5)Ax; = f' f(x)dx2-→0i=1提示若用△A表示任一小区间dA[x,x+Ax]上的窄曲边梯形的面积,Jf(x)则A=Z△A，并取△A~f(x)dx于是A~f(x)dxxx+dx0axA = lim Z f(x)dx= / f(x)dx.4

a b x y o y = f (x) （4） 求极限，得A的精确值 i i n i A =  f x = → lim ( ) 1 0   =  b a f (x)dx 提示 若用A 表示任一小区间 [x, x + x]上的窄曲边梯形的面积， 则A = A，并取A  f ( x)dx， 于是A   f (x)dx A = lim f (x)dx ( ) .  = b a f x dx x x + dx dA 面 积 元 素 4

当所求量U符合下列条件：(1）U 是与一个变量x 的变化区间a,b|有关的量；（2）U对于区间a,b具有可加性，就是说，如果把区间a,b分成许多部分区间，则U相应地分成许多部分量，而U等于所有部分量之和；（3）部分量△U,的近似值可表示为f（)△x;就可以考虑用定积分来表达这个量U5

当所求量U 符合下列条件： （1）U 是与一个变量x 的变化区间a,b 有关 的量； （2）U 对于区间a,b具有可加性，就是 说，如果把区间a,b分成许多部分区间，则 U 相应地分成许多部分量，而U 等于所有部 分量之和； （3）部分量Ui的近似值可表示为 i xi f ( ) ； 就可以考虑用定积分来表达这个量U 5

元素法的一般步骤1）根据问题的具体情况，选取一个变量例如x为积分变量，并确定它的变化区间[a,b]2）设想把区间[a,b]分成n个小区间，取其中任一小区间并记为[x,x+dx]，求出相应于这小区间的部分量△U的近似值.如果△U能近似地表示为[a,b]上的一个连续函数在x处的值f(x)与dx的乘积，就把f(x)dx称为量U的元素且记作dU, 即dU = f(x)dx;6

元素法的一般步骤： 1）根据问题的具体情况，选取一个变量例如 x 为积分变量，并确定它的变化区间[a,b]； 2）设想把区间[a,b]分成 n 个小区间，取其中任 一小区间并记为[x, x + dx]，求出相应于这小区 间的部分量U的近似值.如果U 能近似地表示 为[a,b]上的一个连续函数在x处的值 f (x)与dx 的乘积，就把 f (x)dx称为量U 的元素且记作 dU，即 dU = f (x)dx ； 6

3）以所求量U的元素f(x)dx为被积表达式，在("f(x)dx,区间[a,bl上作定积分，得U=即为所求量U的积分表达式这个方法通常叫做元素法应用方向：平面图形的面积；体积；平面曲线的弧长：功；水压力；引力等

3）以所求量U 的元素 f ( x)dx为被积表达式，在 区间[a,b]上作定积分，得 =  b a U f (x)dx， 即为所求量U 的积分表达式. 这个方法通常叫做元素法． 应用方向： 平面图形的面积；体积；平面曲线的弧长； 功；水压力；引力等． 7

二、小结元素法的提出、思想、步骤（注意微元法的本质）8

元素法的提出、思想、步骤. （注意微元法的本质） 二、小结 8

思考题微元法的实质是什么？9

思考题 微元法的实质是什么？ 9

思考题解答微元法的实质仍是“和式”的极限10

思考题解答 微元法的实质仍是“和式”的极限. 10