《高等数学》课程教学资源（PPT课件）第五章 定积分 5-3 第三节 定积分的换元法和分部积分法

第三节定积分的换元法和分部积分法、定积分的换元法、定积分的分部积分法三、小结吉思考题

第三节 定积分的换元法和分部积分法 一、定积分的换元法 二、定积分的分部积分法 三、小结 思考题

定积分的换元法定理假设(1）f(x)在[a,b]上连续;(2）函数x=Φ(t)在[α,β]上是单值的且有连续导数;(3）当t 在区间[α,β]上变化时，x=(t)的值在[a,b]上变化，且β(α)=a、(β)=b,则 有f" f(x)dx = f f[p(t)]p'(t)dt

假设 （1） f ( x)在[a,b]上连续； 定理 （2）函数x = (t)在[, ]上是单值的且有连续 导数； （3） 当t 在区间[, ]上变化时，x = (t) 的 值 在[a,b]上变化，且() = a、( ) = b， 则 有 f x dx f t t dt b a  =    ( ) [( )] ( ) . 一、定积分的换元法

分析要证[' f(x)dx = f f[p(t)lp'(t)dt由假设知上式两边的被积函数都是连续的.因此两边的定积分都存在,被积函数的原函数也都存在因此,对上式两边的定积分应用牛顿一莱布尼茨公式,转化为证明两边的原函数的增量相等即可

分析 要 证 f x d x f t t d t b a  =    ( ) [( )] ( ) 由假设知,上式两边的被积函数都是连续的,因此两 边的定积分都存在,被积函数的原函数也都存在. 因此,对上式两边的定积分应用牛顿—莱布尼茨公 式,转化为证明两边的原函数的增量相等即可

证设F(x)是f(x)的一个原函数[" f(x)dx = F(b) - F(a),: Φ(t) = F[p(t)ldFdxΦ'(t) :f(x)@'(t)=fo(t)lo(t)三dx dt:. Φ(t)是f[(t)l'(t)的一个原函数[ f[β(t)]p'(t)dt = Φ(β) -Φ(α)

证 设F(x)是 f (x)的一个原函数， f (x)dx F(b) F(a), b a = −  (t) = F[(t)], dt dx dx dF (t) =  = f (x)(t)= f [(t)](t), [( )]( ) = () − (),    f t t dt (t)是 f[(t)](t)的一个原函数

p(α)=a、(β)=b,Φ(β)-(α) = F[β(β)]- F[β(α)I= F(b)- F(a),[f(x)dx = F(b) - F(a) = Φ(β)-@(α)flo(t)lp'(t)dt.注意当α>β时，换元公式仍成立

() = a、( ) = b, ( ) − () = F[( )]− F[()] = F(b) − F(a), f (x)dx F(b) F(a) b a = − = ( ) − () f [ (t)] (t)dt.  =      注 意 当   时，换元公式仍成立

应用换元公式时应注意：(1）用x =β(t)把变量x 换成新变量 时，积分限也相应的改变(2)求出,f[(t)l'(t)的一个原函数Φ(t)后，不必象计算不定积分那样再要把Φ(t)变换成原变量x的函数，而只要把新变量 的上、下限分别代入Φ(t)然后相减就行了配元不换限(3）换元公式也可反过来使用，即β [p(t)lp'(t) dt= ~f(x)dx(令 x = (t))7或配元f[p(t)]p'(t) dt = [~ f[ p(t)1 d p(t)

应用换元公式时应注意: (1) 求出 f [(t)](t)的一个原函数(t)后，不 必象计算不定积分那样再要把(t)变换成原 变量x 的函数，而只要把新变量t 的上、下限 分别代入(t)然后相减就行了. (2) 用x = (t)把变量x 换成新变量t 时，积分限也 相应的改变. (3) 换元公式也可反过来使用 , 即 f x x (令 x = (t)) b a ( )d  = 或配元 (t) d(t) (t) (t) (t) (t) 配元不换限

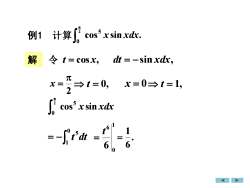
2-计算例1cos' x sin xdx.0解令 t=cosx,dt = -sin xdx,元t= 0,x=0=t=1x225cos' x sin xdx10D1

例1 计算 cos sin . 2 0 5   x xdx 解 令 t = cos x, 2  x =  t = 0, x = 0 t = 1,   2 0 5 cos x sin xdx = − 0 1 5 t dt 1 0 6 6 t = . 6 1 = dt = −sin xdx

"sin'x - sinxdx.例2计算分析：f(x)=/sin'x-sin'x=|cosx(sinx)"cos x(sinx)2dxVsin x - sin xdx =Je cos x(sin x) dx - f cos x(sin x) dx102元32(sinx)d sinx -1[" (sin x)2d sin x-J022242sinxsin5720

例2 计算 分析 sin sin . 0 3 5   x − xdx f x x x 3 5  ( ) = sin − sin ( )2 3 = cos x sin x    − 0 3 5 sin x sin xdx ( )   = 0 2 3 cos x sin x dx ( )   = 2 0 2 3 cos x sin x dx ( )   −  2 2 3 cos x sin x dx ( )   = 2 0 2 3 sin x d sin x ( )   −  2 2 3 sin x d sin x ( ) 2 0 2 5 sin 5 2  = x ( )   − 2 2 5 sin 5 2 x . 5 4 =

3dxe4例3计算x/In x(1 - In x)3d(lnx)04分析原式=fe/Inx(1 - Inx)33d(lnx)d/InxIn x(1- lnx)1-(/lnx)3T 2arcsin(/In x)6

例3 计算 分析 . ln (1 ln ) 4 3  − e e x x x dx 原式  − = 4 3 ln (1 ln ) e (ln ) e x x d x  − = 4 3 ln (1 ln ) e (ln ) e x x d x  − = 4 3 2 1 ( ln ) ln 2 e e x d x   4 3 2 arcsin( ln ) e e = x . 6  =

1adx.(a>0)例4计算x+a?x解dx = acos tdt,令x=asint,元x=0=t=0.tx=a=2元acost2原式 =dt1asint+ a?(1-sin't)元costcost - sint22dt1+dt2 JoJ0sint +costsint + cos t元元元[nsin t+ cos = ".2 22

例4 计算 解   + − a dx a x a x 0 2 2 . ( 0) 1 令 x = asint, x = a , 2   t = x = 0  t = 0, dx = acostdt, 原式   + − = 2 0 2 2 sin (1 sin ) cos dt a t a t a t   + = 2 0 sin cos cos dt t t t         + − = + 2 0 sin cos cos sin 1 2 1 dt t t t t   2 0 lnsin cos 2 1 2 2 1  + +  =  t t . 4  =