《高等数学》课程教学资源（PPT课件）第二章 导数与微分 2-01 第一节 导数的概念

第一节导数的概念引例导数定义导数的几何意义可导与连续的关系小结

◼ 引例 ◼ 导数定义 ◼ 导数的几何意义 ◼ 可导与连续的关系 ◼ 小结 第一节 导数的概念

引例一例1直线运动的瞬时速度问题一质点作直线运动，已知路程S与时间t的关系 s = s(t).试确定tO时的瞬时速度v(tO)解从时刻→+△质点走过的路程As = s(t + △t) - s(to),As这段时间内的平均速度(△t)△t若运动是匀速的，平均速度就等于质点在每个时刻的速度

例1 直线运动的瞬时速度问题 一质点作直线运动,已知路程 s 与时间 t 的 试确定t0时的瞬时速度v(t0). ( ) ( ), 0 0 s = s t + t − s t 这段时间内的平均速度 v(t) 在每个时刻的速度. 解 . t s   = 若运动是匀速的,平均速度就等于质点 关系 s = s(t). 质点走过的路程 一、引例 , 0 0 从时刻 t → t + t

若运动是非匀速的,平均速度△t)是这段时间内运动快慢的平均值,△ 越小它越近似的表明to时运动的快慢.因此，人们把to时的速度定义为Ass(to +△t)-s(to)limv(fo) = lim AtAtt-→0并称之为t时的瞬时速度t)注此式既是它的定义式，文指明了它的计算方法，瞬时速度是路程对时间的变化率

此式既是它的定义式,又指明了它的计算 它越近似的 定义为 v(t 0 ) = , ( ) ( ) lim 0 0 0 t s t t s t t  +  − =  → 并称之为t0时的瞬时速度v(t0 ). 瞬时速度是路程对时间的变化率. 若运动是非匀速的,平均速度 v(t) 是这段 时间内运动快慢的平均值, t 越小, 表明 t0 时运动的快慢.因此, 人们把 t0时的速度 注 方法, t s   0 lim Dt®

例2曲线的切线斜率问题若已知平面曲线y=f(x),如何作过曲线上点M.(xo，f(x的切线呢初等数学中并没有给出曲线切线的定义我们知道与圆周有唯一交点的直线即为圆周过该点的切线.但此定义不适应其它曲线.如与抛物线有唯一交点的直线不一定是切线对于一般曲线如何定义其切线呢？法国数学家费马在1629年提出了如下的定义和求法，从而圆满地解决了这个问题切线位置割线的极限位置

例2 割线的极限位置—— 对于一般曲线如何定义其切线呢? 曲线的切线斜率问题 若已知平面曲线 y = f (x), ( , ( )) 0 0 x0 M x f 如何作过 的切线呢. 初等数学中并没有给出曲线切线的定义. 过该点的切线. 我们知道与圆周有唯一交点的直线即为圆周 但此定义不适应其它曲线. 如 与抛物线有唯一交点的直线不一定是切线. 切线位置. 曲线上点 法国 数学家费马在1629年提出了如下的定义和求 法,从而圆满地解决了这个问题

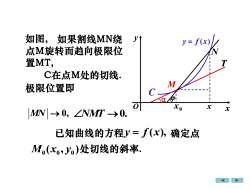
如图，如果割线MN绕Vy= f(x)点M旋转而趋向极限位置MT,TC在点M处的切线M极限位置即C@laxoxxMN|-→0, ZNMT →0.已知曲线的方程y=f(x)，确定点M.(xo,Jo)处切线的斜率

x0 ( , ) 处切线的斜率. 0 0 0 M x y 已知曲线的方程 确定点 如果割线MN绕 点M旋转而趋向极限位 置MT, 极限位置即 MN → 0, C在点M处的切线. 如图, NMT →0. y = f (x), x   T x y O y = f ( x) C N • M

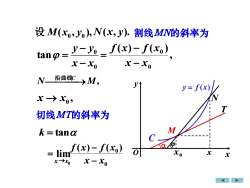
设 M(xo,yo),N(x,y).割线MN的斜率为。f(x)- f(xo)y-yotan @ = -x-xox-xo沿曲线CN.>M,ytV=x→xo'T切线MT的斜率为Mk =tanαCOYQ1f(x)- f(xo)可xox= limxx→xox-xo

( , ), 0 0 设 M x y 0 0 tan x x y y − −  = , ( ) ( ) 0 0 x x f x f x − − = N k = tan 0 0 ( ) ( ) x x f x f x − − = N(x, y). 割线MN的斜率为 , x → x0 切线MT的斜率为 ⎯沿曲线 ⎯⎯C →M, x0 x   T x y O y = f ( x) C N • M 0 lim x→x

上述两例，就其实际意义来说各不相同，分别属于运动学、几何学中的问题，但在数量关系上确有如下的共性1在问颠提注上都其已知一个函V三x)娄在现实生活中，凡涉及变化率的问题，其精确描述和计算都离不开此式所规定的这一运算。(2)当变化是非作平均变化率的Ayf(x。 +△x)- f(x)lim极限运算：limAr→0 △xAxr-→0△x

y = f (x), 就其实际意义来说各不相同, 关系上确有如下的共性: 但在数量 1. 在问题提法上,都是已知一个函 数求y关于x在x0处的变化率. 2. 计算方法上, (1) 当y随 x均匀变化时,用除法. (2) 当变化是非均匀的时,需作平均变化率的 x y x    →0 lim 在现实生活中,凡涉及变化率的问 题,其精确描述和计算都离不开此式所 规定的这一运算. 上述两例, 分别属于运动学、几何学中的问题, x f x x f x x  +  − =  → ( ) ( ) lim 0 0 0 极限运算:

二、导数的定义定义设函数y= f(x)在点x的某个邻域内有定义,当自变量从x,变到 x。+ △x 时,函数= f(x)的增量Ay= (x+△x)-f(x)与自变量的增量△x之比Ay - f(x +Ax)- f(x)AxAx称为f(x)的平均变化率

定义 设函数 y = f ( x)在 点x0的某个邻域内 x f x x f x x y  +  − =   ( ) ( ) 0 0 称 为f ( x)的 , 当自变量从 x0 变 到 x0 + x 时 ( ) ( ) ( ) 0 0 y = f x 的增量y = f x + x − f x 函数 变量的增量x 之 比 与自 平均变化率. 有定义, 二、导数的定义

函数在一点x.处的变化率如△x→0,平均变化率的极限：Ayf(x +A)- f(x)(1)limlimAr-→0ArAr→0 △x存在,则称此极限值为f(x)在x,处的导数并说f(x)在x,处可导或有导数.可用下列记号dydf(x)或, f'(x)x=xodxdxlx=xoX=Xo中的任何一个表示,如f(xo + △x)- f(xo)f'(x)= lim Ax4x-→>0

如x →0, 并说f (x)在x0 处可导 , 0 x x y =  ( ) x0 f  中的任何一个表示, f (x0 ) = x y   存在, 如 平均变化率的极限: (1) ( ) ( ) lim 0 0 0 x f x x f x x  +  − = 0  → lim x→ ( ) . f x 在x0 处的导数 , 或 d d x x0 x y = 0 d d ( ) x x x f x = x f x x f x x    ( ) ( ) lim 0 0 0 + − → 函数在一点 x0 处的变化率 或有导数.可用下列记号 则称此极限值为

f(xo +△x) - f(xo)(1)f'(xo)= limAv0Ax当极限(1)式不存在时,就说函数 f (x)在xo处不可导或导数不存在.特别当(1)式的极限为正(负)无穷时有时也说在处导数是正(负)无穷大，但这时导数不存在在利用导数的定义证题或计算时,要注意注导数定义可以写成多种形式：f(xo +h)- f(xo)f'(xo) = limhh0f(xo-h )- f(xo)f'(xo) = lim-h-0

处不可导或导数不存在. 特别当(1)式的极限为 有时也说在x0处导数是正(负)无 注 要注意 导数定义可以写成多种形式: , ( ) ( ) ( ) lim 0 0 0 0 f x f x f x + −  = → . ( ) ( ) ( ) lim 0 0 0 0 f x f x f x −  = → 当极限(1)式不存在时, 就说函数 f (x)在x0 在利用导数的定义证题或计算时, 正(负)无穷时, 穷大,但这时导数不存在. (1) ( ) ( ) ( ) lim 0 0 0 0 x f x x f x f x x  +  −  =  → x x x h h h − h − h − h