《高等数学》课程教学资源（PPT课件）第一章 函数与极限 1-08 第八节 函数的连续性与间断点

第八节函数的连续性与间断点函数的连续函数的间断点小结思考题

1 第八节 函数的连续性与间断点 ◼ 函数的连续 ◼ 函数的间断点 ◼ 小结 思考题

在自然界中,许多事物的变化是连续的,如气温变化很小时，单摆摆长变化也很小。时间变化很小时，生物生长的也很少。这种现象在函数关系上的反映就是函数的连续性。在高等数学中，主要的研究对象就是连续函数。从直观上不妨这样说，连续函数的特征就是它的图形是连续的，也就是说，可以一笔画成

在自然界中,许多事物的变化是连续的,如 气温变化很小时，单摆摆长变化也很小。时间 变化很小时，生物生长的也很少。这种现象在 函数关系上的反映就是函数的连续性。在高等 数学中，主要的研究对象就是连续函数。从直 观上不妨这样说，连续函数的特征就是它的图 形是连续的，也就是说，可以一笔画成

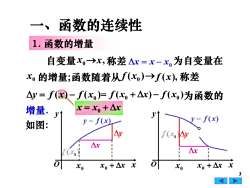
一、函数的连续性1.函数的增量自变量Xo→x,称差△x= x-x为自变量在xo的增量;函数随着从f(xo)→f(x),称差Ay=f(x)f(x)=f(x+△x)-f(xo)为函数的x=x.+Ar增量.VV=f(x)y=f(x)如图：AyAyArAx可可Xo + Ax xXo+Ar xxoxo3公

3 1. 函数的增量 ( ) ( ) x0 y = f x − f 自变量 0 x →x, 称差 为自变量在 0 x 的增量;函数随着从 ( ) x0 f →f ( x), 称差 ( ) ( ) 0 x0 = f x + x − f 为函数的 增量. 如图: x = x0 + x 一、函数的连续性 x y O x y O 0 x x0 + x 0 x x0 + x

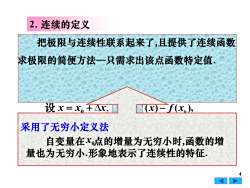
2.连续的定义把极限与连续性联系起来了，且提供了连续函数求极限的简便方法一一只需求出该点函数特定值设x=x.+x(x)-f(x),采用了无穷小定义法自变量在x点的增量为无穷小时，函数的增量也为无穷小.形象地表示了连续性的特征

则称函数 在 处 0 x f (x) f (x) f (x) x0 f x( ) 0 x 4 连续, 2. 连续的定义 , 0 设 x x x = +  ( ) ( ), x0 y = f x − f x → 0 定义1 设函数 在 ( ) U x0 内有定义,若 lim 0 0  =  → y x 则称函数 在 处 并称 为函数 的 连续点. y → 0 定义2 若 lim ( ) ( ), 0 0 f x f x x x = → 连续. 充分必要条件 把极限与连续性联系起来了,且提供了连续函数 求极限的简便方法—只需求出该点函数特定值. 自变量在 点的增量为无穷小时,函数的增 量也为无穷小.形象地表示了连续性的特征. 采用了无穷小定义法 x0

定义3(-)>0,>0,使当xxl<时,恒有f(x)-f(x)<把极限定义严密化，便于分析论证连续性的三种定义形式不同，但本质相同这三种定义中都含有三个要素：(1) f(x)在U。(x)内有定义;(2) lim f(x)存在;x→x(3) lim f(x) = f(xo)x→xo5A

5 连续性的三种定义形式不同,但本质相同. 这三种定义中都含有三个要素: f (x)在 ( ) (1) U x0 内有定义; lim ( ) 0 f x x→x (2) lim ( ) 0 f x x→x (3) ( ) x0 = f 把极限定义严密化,便于分析论证. 存在; 定义3 ( −  )    0 , , 使 当 x − x0   时    0 , ( ) ( ) . 0 恒 有 f x − f x  

注由上述定义可知，fx)在xo点的连续性是描述,f(x)在xo点邻域的性态的.即它是对某一邻域而言.因此在孤立点处无连续可言般讲,证明的命题用函数连续的定义1方便；判断函数在某点是否连续，尤其是判断分段函数在分界点处是否连续用定义2方便

6 注 由上述定义可知, f(x)在x0点的连续性 是描述 f(x)在x0点邻域的性态的.即它是对某 一邻域而言.因此在孤立点处无连续可言. 一般讲,证明的命题用函数连续的定义1方 便;判断函数在某点是否连续,尤其是判断分 段函数在分界点处是否连续用定义2方便

A函数的连续性与间断点imaoANom例证明y= sinx 函数在区间(-oo,+oo）内连续证任取x E(-00,+),Ay= sin(x + Ax) -sin xAxArAxAxArsin≤2-1sincos(x +22222Ax4x → 0=|4x?即lim △y = 00≤1cos(x24x→0即函数 = sinx对任意xE(-oo,+)都是连续的类似可证，函数 = cos x 在区间(-0,+oo)内是连续的

7 例 证明 函数在区间 内连续. 证 任取 y = ) 2 cos( 2 2sin x x x   +  = ) 1 2 cos( +  x x  sin( x + x) −sin x lim 0 0  =  → y x 0 即 函数的连续性与间断点 y x = sin ( , ) − + x  − + ( , ), 即函数 对任意 都是连续的. 类似可证，函数 在区间 内是 连续的. y x = sin x − + ( , ) y x = cos ( , ) − + =  x  x → 0 2 2 sin x x  lim 0 0 = → y x  

定义2limf(x)=f(x）X-1x0,xsin在x= 0例 试证函数f(x)x0,x=0,处连续。证 ：:limxsin-0.x-→0x又 f(0) = 0, lim f(x)= f(0),函数f(x)在x=0处连续D

8 定义2 lim ( ) 0 f x x→x ( ) x0 = f 例 0 0, 0, , 0, 1 sin ( ) =     =  = x x x x x f x 在 证 = → x x x 1 lim sin 0  又 f (0) = 0, 函数 f x x ( ) . 在 = 0处连续 lim ( ) (0), 0 f x f x = → 0, 试证函数 处连续

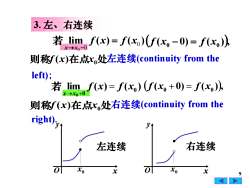
3.左、右连续若 lim f(x)= f(x)(f(x-0)= f(x))则称f（x）在点x.处左连续（continuityfromtheleft);若 lim f(x)= f(x) (f(x +0)= f(x))x-x+0则称f(x)在点x.处右连续(continuityfromtheright)V右连续左连续oTo1XoxoxxA

9 3. 左、右连续 0 0 0 lim ( ) ( ) x x f x f x → − 若 = 则称f (x)在点x0 处 lim ( ) ( ) 0 0 0 f x f x x x = → + 若 则称f (x)在点x0 处 ( ( 0) ( )), 0 x0 f x − = f ( ( 0) ( )), 0 x0 f x + = f 左连续(continuity from the 右连续(continuity from the left); right). 0 x 左连续 0 x 右连续 x y O x y O

函数f(x)在x处连续定理1函数f(x)在xo处既左连续又右连续(f(x, -0) = f(x, +0) = f(x))此定理常用于判定分段函数在分段点处的连续性10

10 定理1 此定理常用于判定分段函数在分段点 处的连续性 ( ( 0) ( 0) ( )) 0 0 x0 f x − = f x + = f 函数 在 处连续 函数 在 处既左连续又右连续. f x( ) x0 f x( ) x0