《高等数学》课程授课教案（讲义）第八章 多元函数微分法及其应用

第八章多元函数微分法及其应用第一节：多元函数的基本概念教学目的：学习并掌握关于多元函数的区域、极限以及多元函数概念，掌握多元函数的连续性定理，能够判断多元函数的连续性，能够求出连续函数在连续点的极限。教学重点：多元函数概念和极限，多元函数的连续性定理。教学难点：计算多元函数的极限。教学内容：第一节多元函数的基本概念一区域讨论一元函数时，经常用到邻域和区间的概念。由于讨论多元函数的需要，我们首先把邻域和区间概念加以推广，同时还要涉及其它一些概念。1．邻域设p(xo,yo）是xoy平面上的一个点，是某一正数。与点P。(xoyo）距离小于的点p(x,y)的全体，称为点P。的邻域，记为U(Po,)，即U(Po,0)=(PPP/ 0为半径的圆的内部的点P(x,y)的全体。2.区域设E是平面上的一个点集，P是平面上的一个点。如果存在点P的某一邻域U(P)CE，则称P为E的内点（画图8-1显示）。显然，E的内点属于E

第 八 章 多元函数微分法及其应用 第 一 节：多元函数的基本概念 教学目的：学习并掌握关于多元函数的区域、极限以及多元函数概念，掌握多元 函数的连续性定理，能够判断多元函数的连续性，能够求出连续函数 在连续点的极限。 教学重点：多元函数概念和极限，多元函数的连续性定理。 教学难点：计算多元函数的极限。 教学内容： 第一节 多元函数的基本概念 一、 区 域 讨论一元函数时，经常用到邻域和区间的概念。由于讨论多元函数的需要，我们首先 把邻域和区间概念加以推广，同时还要涉及其它一些概念。 1． 邻域 设 ( , ) 0 0 0 p x y 是 xoy 平面上的一个点，δ 是某一正数。与点 ( , ) 0 0 0 p x y 距离小于δ 的 点 p(, ) x y 的全体，称为点 P0 的δ 邻域，记为 ( , ) U P0 δ ，即 ( , ) U P0 δ ={ } P PP0 0 为半径的圆的内 部的点 P(x, y) 的全体。 2． 区域 设 E 是平面上的一个点集，P 是平面上的一个点。如果存在点 P 的某一邻域U(P) ⊂ E ， 则称 P 为 E 的内点（画图 8-1 显示）。显然， E 的内点属于 E

如果E的点都是内点，则称E为开集。例如，点集E,=((x,y)0)及(x,y)l0)是无界开区域。3.n维空间我们知道，数轴上的点与实数有一一对应关系，从而实数全体表示数轴上一切点的集合，即直线。在平面上引入直角坐标系后，平面上的点与二元数组（x,y）一一对应，从而二元数组（xy）全体表示平面上一切点的集合，即平面。在空间引入直角坐标系后，空间的点与三元数组（xy,z）一一对应，从而三元数组（x，y,=）全体表示空间一切点的集合，即空间。一般地，设n为取定的一个自然数，我们称n元数组（x，r2，",x，）的全体为n维空间，而每个n元数组(x,x2，",x,）称为n维空间中的一个点，数x称为该点的第i个坐标。n维空间记为R"。n维空间中两点P(x,X2",x）及Q(x,X2，",x）间的距离规定为

如果 E 的点都是内点，则称 E 为开集。例如，点集 {( , )1 4} 2 2 E1 = x y 0}及{( , )1 4} 2 2 x y 0}是无界开区域。 3． n 维空间 我们知道，数轴上的点与实数有一一对应关系，从而实数全体表示数轴上一切点的集合， 即直线。在平面上引入直角坐标系后，平面上的点与二元数组(x, y)一一对应，从而二元数 组(x, y)全体表示平面上一切点的集合，即平面。在空间引入直角坐标系后，空间的点与三 元数组（ x, y,z ）一一对应，从而三元数组（ x, y,z ）全体表示空间一切点的集合，即空间。 一般地，设 n 为取定的一个自然数，我们称n 元数组（ n x , x , , x 1 2 " ）的全体为 n 维空间， 而每个 n 元数组( , , , ) 1 2 n x x " x 称为 n 维空间中的一个点，数 xi 称为该点的第 i 个坐标。n 维 空间记为 Rn 。 n 维空间中两点 ( , , , ) 1 2 n P x x " x 及 ( , , , ) 1 2 n Q x x " x 间的距离规定为

[Pg| = /(y -x,)2 +(y2 -x,)2 +...+(y, -x,)。容易验知，当n=1，2，3时，由上式便得解析几何中关于直线（数轴），平面，空间内两点的距离。前面就平面点集来陈述的一系列概念，可推广到n维空间中去。例如，设P。ER”，是某一正数，则n维空间内的点集U(Po,0)=(PPP0,h>0)内取定一对值(r,h)时，V的对应值就随之确定。例2一定量的理想气体的压强P、体积V和绝对温度T之间具有关系RTp=V'其中R为常数。这里，当V、T在集合(V,T)V>0,T>O)时，p的对应值就随之确定。例3设R是电阻R、R并联后的总电阻，由电学知道，它们之间具有关系R,R,R=-R, + R2对应值就随之确定。上面三个例子的具体意义虽各不相同，但它们却有共同的性质，抽象出这些共性就可得出以下二元函数的定义。定义一设D是平面上的一个点集。如果对于每个点P(x,Jy)eD，变量z按照一定法则总有确定的值和它对应，则称z是变量x、y的二元函数（或点P的函数），记为z= f(x,y) (或z=f(P))

2 2 2 2 2 1 1 ( ) ( ) ( ) n n PQ = y − x + y − x +"+ y − x 。 容易验知，当 n =1，2，3 时，由上式便得解析几何中关于直线（数轴），平面，空间内两点 的距离。 前面就平面点集来陈述的一系列概念，可推广到 n 维空间中去。例如，设 n P0 ∈ R ，δ 是某一正数，则 n 维空间内的点集 ( , ) U P0 δ ={ , } 0 n P PP 0, h > 0}内取定一对值(r,h) 时，V 的对应值就随之确定。 例 2 一定量的理想气体的压强 p 、体积V 和绝对温度T 之间具有关系 p = V RT ， 其中 R 为常数。这里，当V 、T 在集合{(V,T)V > 0,T > 0}时， p 的对应值就随之确定。 例 3 设 R 是电阻 R1、 R2 并联后的总电阻，由电学知道，它们之间具有关系 1 2 1 2 R R R R R + = 对应值就随之确定。 上面三个例子的具体意义虽各不相同，但它们却有共同的性质，抽象出这些共性就可 得出以下二元函数的定义。 定义一 设 D 是平面上的一个点集。如果对于每个点 P(x, y) ∈ D ，变量 z 按照一定法 则总有确定的值和它对应，则称 z 是变量 x、y 的二元函数（或点 P 的函数），记为 z = f (x, y) （或 z = f (P) ）

点集D称为该函数的定义域，X、y称为自变量，z也称为因变量。数集(=z = f(x,y),(x,y)e D)称为该函数的值域。z是x,y的函数也可记为z=z(x,y)，z=Φ(x,y)等等。类似地可以定义三元函数u=f(x,J,=)以及三元以上的函数。一般的，把定义1中的平面点集D换成n维空间内的点集D，则可类似地可以定义n元函数u=f(x,x2,",x）。n元函数也可简记为u=f(P)，这里点P(x,x2,"",x）eD。当n=1时，n元函数就是一元函数。当n≥2时，n元函数就统称为多元函数。关于多元函数定义域，与一元函数类似，我们作如下约定：在一般地讨论用算式表达的多元函数u=f(P)时，就以使这个算式有确定值u的自变量所确定的点集为这个函数的定义域。例3，求下列函数的定义域1. z= ln(x+y)解：函数z=ln(x+y)的定义域为((x+y)x+y>0)（图8-3），就是一个无界开区域。2. z=arcsin(x2 +y)解：函数z=arcsin(x2+y）的定义域为(x+ y)x? + y? ≤1)（图8-4），这是一个闭区域。x+y=0

点集 D 称为该函数的定义域， x、y 称为自变量， z 也称为因变量。数集 {z z = f (x, y),(x, y) ∈ D} 称为该函数的值域。 z 是 x, y 的函数也可记为 z = z(x, y) ， z = Φ(x, y)等等。 类似地可以定义三元函数u = f (x, y,z) 以及三元以上的函数。一般的，把定义 1 中的 平面点集 D 换 成 n 维空间内的点集 D ，则可类似地可以定义 n 元函数 ( , , , ) 1 2 n u = f x x " x 。 n 元函数也可简记为u = f (P) ，这里点 P(x1 , x2 ,", xn ) ∈ D 。当 n = 1时， n 元函数就是一元函数。当 n ≥ 2时，n 元函数就统称为多元函数。 关于多元函数定义域，与一元函数类似，我们作如下约定：在一般地讨论用算式表达 的多元函数u = f (P) 时，就以使这个算式有确定值 u 的自变量所确定的点集为这个函数的 定义域。 例 3，求下列函数的定义域 1． z = ln(x + y) 解 ：函数 z = ln(x + y)的定义域为 {(x + y) x + y > 0} （图 8-3），就是一个无界开区域。 2． arcsin( ) 2 2 z = x + y 解 ：函数 arcsin( ) 2 2 z = x + y 的定义域为 {( ) 1} 2 2 x + y x + y ≤ （图 8-4），这是一个闭区域。 x+y=0

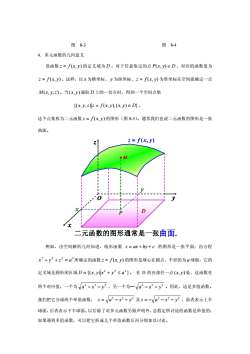
图8-4图8-34.多元函数的几何意义设函数z=f(x,y)的定义域为D。对于任意取定的点 P(x,y)eD，对应的函数值为z=f(x,y)。这样，以x为横坐标、为纵坐标、z=f(x,y)为竖坐标在空间就确定一点M(x,y,z)。当(x,y)遍取D上的一切点时，得到一个空间点集((x,y,=)z= f(x,y),(x,y)e D) ,这个点集称为二元函数z=f(x,y）的图形（图8-5)。通常我们也说二元函数的图形是一张曲面。z = f(x,y)Z2y二元函数的图形通常是一张曲面例如，由空间解析几何知道，线形函数z=ax+by+c的图形是一张平面；由方程x2+y?+=2=α所确定的函数z=f(x,J)的图形是球心在圆点、半径的为α球面，它的定义域是圆形闭区域D=(x,J)x2+y2≤α2)。在D的内部任一点(x,J)处，这函数有两个对应值，一个为a2-x2-y2，另一个为一a2-x2-y2。因此，这是多值函数。我们把它分成两个单值函数：z=a2-x?-y2及z=-a2-x-y，前者表示上半球面，后者表示下半球面。以后除了对多元函数另做声明外，总假定所讨论的函数是单值的；如果遇到多值函数，可以把它拆成几个单值函数后再分别加以讨论

4．多元函数的几何意义 设函数 z = f (x, y) 的定义域为 D 。对于任意取定的点 P(x, y) ∈ D ，对应的函数值为 z = f (x, y) 。这样，以 x 为横坐标、 y 为纵坐标、z = f (x, y) 为竖坐标在空间就确定一点 M (x, y,z) 。当(x, y)遍取 D 上的一切点时，得到一个空间点集 {(x, y,z) z = f (x, y),(x, y) ∈ D}， 这个点集称为二元函数 z = f (x, y) 的图形（图 8-5）。通常我们也说二元函数的图形是一张 曲面。 二元函数的图形通常是一张曲面. z = f (x, y) D x y z O • M x y P 例如，由空间解析几何知道，线形函数 z = ax + by + c 的图形是一张平面；由方程 2 2 2 2 x + y + z = a 所确定的函数 z = f (x, y) 的图形是球心在圆点、半径的为 a 球面，它的 定义域是圆形闭区域 {( , ) } 2 2 2 D = x y x + y ≤ a 。 在 D 的内部任一点(x, y)处，这函数有 两个对应值，一个为 2 2 2 a − x − y ，另一个为— 2 2 2 a − x − y 。因此，这是多值函数。 我们把它分成两个单值函数： 2 2 2 z = a − x − y 及 2 2 2 z = − a − x − y ，前者表示上半 球面，后者表示下半球面。以后除了对多元函数另做声明外，总假定所讨论的函数是单值的； 如果遇到多值函数，可以把它拆成几个单值函数后再分别加以讨论。 图 8-3 图 8-4

三、多元函数的极限我们先讨论二元函数z=f(x,y)当x→x，→yo，即P(x,y)→P(xo,yo)时的极限。这里P一→>P。表示点P以任何方式趋于点P，也就是点P与点P。间的距离趋于零，即PP=(x-x)+(y-y)→0。与一元函数的极限概念类似，如果在P(x,J)→P(xo,Jo）的过程中，对应的函数值f(x,y)无限接近一个确定的常数A，我们就说A是函数x→xo，→y时的极限。下面用“-”语言描述这个极限概念。定义2设函数f(x,y)在开区域（或闭区域）D内有定义，P(xo,yo）是D的内点或边界点。如果对于任意给定的正数ε，总存在正数，使得对于适合不等式00，取=，则当0(x-0)+(y-0)2时，总有x?+y2)sin<8成立x+y所以lim f(x,y) = 0我们必须注意，所谓二重极限存在，是指P(x,y)以任何方式趋于P(x,y)时，函数都

三、多元函数的极限 我们先讨论二元函数 z = f (x, y) 当 0 x → x ， 0 y → y ，即 ( , ) ( , ) 0 0 0 P x y → P x y 时的 极限。 这里 P → P0 表示点 P 以任何方式趋于点 P0 ，也就是点 P 与点 P0 间的距离趋于零， 即 ( ) ( ) 0 2 0 2 PP0 = x − x0 + y − y → 。 与一元函数的极限概念类似，如果在 ( , ) ( , ) 0 0 0 P x y → P x y 的过程中，对应的函数值 f (x, y) 无限接近一个确定的常数 A ，我们就说 A 是函数 0 x → x ， 0 y → y 时的极限。下面 用“ε − δ ”语言描述这个极限概念。 定义 2 设函数 f (x, y) 在开区域（或闭区域）D 内有定义， ( , ) 0 0 0 P x y 是 D 的内点或 边界点。如果对于任意给定的正数 ε ，总存在正数 δ ，使得对于适合不等式 0，取δ = ε ，则当 < − + − < δ 2 2 0 (x 0) ( y 0) 时，总有 − < ε + + 0 1 ( )sin 2 2 2 2 x y x y 成立 所以 lim ( , ) 0 0 = → f x y x x 我们必须注意，所谓二重极限存在，是指 P(x, y) 以任何方式趋于 ( , ) 0 P x y 时，函数都

无限接近于A。因此，如果P(x,y)以某一种特殊方式，例如沿着一条直线或定曲线趋于P。（x，y)时，即使函数无限接近于某一确定值，我们还不能由此断定函数的极限存在。但是反过来，如果当P(x,y)以不同方式趋于P(x,y)时，函数趋于不同的值，那么就可以断定这函数的极限不存在。下面用例子来说明这种情形。例5.证明函数xyx2+y*+0,f(x,J)=}x + y2,0,x2+y?=0,证：当点P(x.y）沿x轴趋于点（0.0)时，limf(x.0)=lim0=0：又当点P(x.y）x→(沿y轴趋于点(0,0)时，limf(0,y)=lim0=0。~0y-0虽然点P(x,Jy)以上述两种特殊方式(沿x轴或沿y轴)趋于原点时函数的极限存在并且相等，但是limf(x,y)并不存在.这是因为当点P(x,y)沿着直线y=kx趋于点(0,0)130时,有kr2kxy= limlim1+k2o+y?x-0 x2 +ky?显然它是随着k的值的不同而改变的xy例6.极限lim是否存在？28x+y2kx3x'ykx解：取y=kx，x*+y?x*+k2x2=x2+k2kx.. lim f(x,y)=lim=0ox+y30Y当P(x,y)沿x轴的方向无限接近点（0，0）时，lim(x,0)=0当P(x,y)沿y轴的方向无限接近点（0，0）时，limf(O,y)=0xtx'y1取y=kx?,2x*+x4xt+y?故，极限不存在；

无限接近于 A。因此，如果 P(x, y) 以某一种特殊方式，例如沿着一条直线或定曲线趋于 ( , ) 0 P x y 时，即使函数无限接近于某一确定值，我们还不能由此断定函数的极限存在。但是 反过来，如果当 P(x, y) 以不同方式趋于 ( , ) 0 P x y 时，函数趋于不同的值，那么就可以断定 这函数的极限不存在。下面用例子来说明这种情形。 例 5．证明函数 ⎪ ⎩ ⎪ ⎨ ⎧ + = + ≠ = + 0, 0, , 0, ( , ) 2 2 2 2 2 2 x y x y x y xy f x y 证 ：当点 P(x, y) 沿 x 轴趋于点(0,0) 时，lim ( ,0) lim0 0 0 0 = = x→ x→ f x ；又当点 P(x, y) 沿 y 轴趋于点(0,0) 时，lim (0, ) lim0 0 0 0 = = y→ y→ f y 。 虽然点 P(x, y) 以上述两种特殊方式(沿 x 轴或沿 y 轴)趋于原点时函数的极限存在并且 相等,但是lim ( , ) 0 0 f x y y x → → 并不存在.这是因为当点 P(x, y) 沿着直线 y = kx趋于点(0,0) 时,有 2 2 2 2 2 0 2 2 0 0 1 lim lim k k x k y kx x y xy x y kx x + = + = + → = → → ， 显然它是随着 k 的值的不同而改变的. 例 6．极限 2 4 2 0 0 limx y x y → x y → + 是否存在？ 解：取 y = kx ， 2 3 4 2 4 22 2 2 x y kx kx x y x kx x k = = ++ + ( ) 2 2 0 0 lim , lim 0 x x y kx y kx kx f xy → → x y = = ∴ = = + 当 Pxy (, ) 沿 x 轴的方向无限接近点（0，0）时， 0 lim ( ,0) 0 x f x → = 当 Pxy (, ) 沿 y 轴的方向无限接近点（0，0）时， 0 lim (0, ) 0 x f y → = 取 2 y = kx ， 2 4 42 44 1 2 xy x xy xx = = + + 故，极限不存在；

以上关于二元函数的极限概念，可相应的推广到n元函数u=f(P）即u=f(x,x2,"",x)上去。关于多元函数极限的运算，有与一元函数类似的运算法则例 6 求 lim sin(a)x32这里(x,)=sin()在区域D,=(,)0)解：x内都有定义，P(O,2)同时为D,及D，的边界点。但无论在D,内还是在D,内考，下列运算都是正确的：sin(xy)sin(xy)lim=lim2.limy=1.2=2。xxy139xy0+四、多元函数的连续性明白了函数极限的概念，就不难说明多元函数的连续性，定义3设函数f(x,y)在开区域（闭区域）D内有定义，P(xo,y）是D的内点或边界点且PED。如果lim f(x,y)= f(xo,yo),则称函数f(x,y)在点P(xo,yo）连续。如果函数f(x,y)在开区域（或闭区域)D内的每一点连续，那么就称函数f(x,y)在D内连续，或者称f(x,J)是D内的连续函数。以上关于二元函数的连续性概念，可相应地推广到n元函数f（P）上去。若函数f(x,y)在点P(xo,yo)不连续，则称P为函数f(x,y)的间断点。这里顺便指出：如果在开区域（或闭区域）D内某些孤立点，或者沿D内某些曲线，函数f(x,J)没有定义，但在D内其余部分都有定义，那么这些孤立点或这些曲线上的点，都是函数f(x,Jy)的不连续点，即间断点。前面已经讨论过的函数

以上关于二元函数的极限概念 , 可相应的推广到 n 元函数 u = f (P) 即 ( , , , ) 1 2 n u = f x x " x 上去。 关于多元函数极限的运算,有与一元函数类似的运算法则. 例 6 求 x xy y x sin( ) lim 2 0 → → . 解： 这里 x xy f x y sin( ) ( , ) = 在区域 {( , ) 0} D1 = x y x 内都有定义， (0,2) P0 同时为 D1及 D2 的边界点。但无论在 D1内还是在 D2 内考虑，下列运 算都是正确的： lim 1 2 2 sin( ) lim sin( ) lim 0 2 2 0 = ⋅ = ⋅ = → → → → y xy xy x xy xy y y x 。 四、多元函数的连续性 明白了函数极限的概念，就不难说明多元函数的连续性， 定义 3 设函数 f (x, y) 在开区域（闭区域）D 内有定义， ( , ) 0 0 0 P x y 是 D 的内点或边 界点且 P0 ∈ D 。如果 lim ( , ) ( , ) 0 0 0 0 f x y f x y y y x x = → → , 则称函数 f (x, y) 在点 ( , ) 0 0 0 P x y 连续。 如果函数 f (x, y) 在开区域（或闭区域）D 内的每一点连续，那么就称函数 f (x, y) 在 D 内连续，或者称 f (x, y) 是 D 内的连续函数。 以上关于二元函数的连续性概念，可相应地推广到 n 元函数 f (P) 上去。 若函数 f (x, y) 在点 ( , ) 0 0 0 P x y 不连续，则称 P0 为函数 f (x, y) 的间断点。这里顺便指 出：如果在开区域（或闭区域） D 内某些孤立点，或者沿 D 内某些曲线，函数 f (x, y) 没 有定义，但在 D 内其余部分都有定义，那么这些孤立点或这些曲线上的点，都是函数 f (x, y) 的不连续点，即间断点。 前面已经讨论过的函数

xyx2+ y?+0,f(x,jx2 +y21 o,x2 + y2 = 0,当x→x，y→y。时的极限不存在，所以点(0,0)是该函数的一个间断点。二元函数的间断点可以形成一条曲线，例如函数1z = sin -x? + y? -1在圆周x2+y?=1上没有定义，所以该圆周上各点都是间断点。与闭区域上一元连续函数的性质相类似，在有界闭区域上多元连续函数也有如下性质。性质1（最大值和最小值定理）在有界闭区域D上的多元连续函数，在D上一定有最大值和最小值。这就是说，在D上至少有一点P及一点P2，使得f(P）为最大值而f(P2)为最小值，即对于一切PED,有f(P)≤ f(P)≤(P).性质2（介值定理）在有界闭区域D上的多元连续函数，如果在D上取得两个不同的函数值，则它在D上取得介于这两个值之间的任何值至少一次。特殊地，如果μ是函数在D上的最小值m和最大值M之间的一个数，则在D上至少有一点Q，使得f(Q)=μ。一元函数中关于极限的运算法则，对于多元函数仍然适用：根据极限运算法则，可以证明多元连续函数的和、差、积均为连续函数；在分母不为零处，连续函数的商是连续函数，多元连续函数的复合函数也是连续函数。与一元的初等函数相类似，多元初等函数是可用一个式子所表示的多元函数，而这个式子是由多元多项式及基本初等函数经过有限次的四则运算和复合步骤所构成的（这里指出，基本初等函数是一元函数，在构成多元初等函数时，它必须与多元函数复合）。例如X+x?-y?1+x?是两个多项式之商，它是多元初等函数。又例如sin(x+y)是由基本初等函数sinμ与多项式u=x+y复合而成的，它也是多元初等函数，根据上面指出的连续函数的和、差、积、商的连续性以及连续函数的复合的连续性再考虑到多元多项式及基本初等函数的连续性，我们进一步可以得出如下结论：

⎪ ⎩ ⎪ ⎨ ⎧ + = + ≠ + 0, 0, , 0, ( , ) 2 2 2 2 2 2 x y x y x y xy f x y 当 0 x → x ， 0 y → y 时的极限不存在，所以点(0,0) 是该函数的一个间断点。二元函数的间 断点可以形成一条曲线，例如函数 1 1 sin 2 2 + − = x y z 在圆周 1 2 2 x + y = 上没有定义，所以该圆周上各点都是间断点。 与闭区域上一元连续函数的性质相类似，在有界闭区域上多元连续函数也有如下性质。 性质 1（最大值和最小值定理） 在有界闭区域 D 上的多元连续函数，在 D 上一定有 最大值和最小值。这就是说，在 D 上至少有一点 P1 及一点 P2 ，使得 ( ) P1 f 为最大值而 ( ) P2 f 为最小值，即对于一切 P∈D, 有 ( ) ( ) ( ) 2 P1 f P ≤ f P ≤ f . 性质 2（介值定理） 在有界闭区域 D 上的多元连续函数，如果在 D 上取得两个不同的 函数值，则它在 D 上取得介于这两个值之间的任何值至少一次。特殊地，如果 μ 是函数在 D 上的最小值 m 和最大值 M 之间的一个数，则在 D 上至少有一点Q ，使得 f (Q) = μ 。 一元函数中关于极限的运算法则，对于多元函数仍然适用；根据极限运算法则， 可以 证明多元连续函数的和、差、积均为连续函数；在分母不为零处，连续函数的商是连续函数。 多元连续函数的复合函数也是连续函数。 与一元的初等函数相类似，多元初等函数是可用一个式子所表示的多元函数，而这个 式子是由多元多项式及基本初等函数经过有限次的四则运算和复合步骤所构成的（这里指 出，基本初等函数是一元函数，在构成多元初等函数时，它必须与多元函数复合）。例如， 2 2 2 1 x x x y + + − 是两个多项式之商，它是多元初等函数。又例如sin(x + y)是由基本初等函数sin μ 与多项 式 μ = x + y 复合而成的，它也是多元初等函数。 根据上面指出的连续函数的和、差、积、商的连续性以及连续函数的复合的连续性， 再考虑到多元多项式及基本初等函数的连续性，我们进一步可以得出如下结论：

-切多元初等函数在其定义区域内是连续的。所谓定义区域是指包含在定义域内的区域或闭区域。由多元初等函数的连续性，如果要求它在点P。处的极限，而该点又在此函数的定义区域内，则极限值就是函数在该点的函数值，即lim f(P)= f(Po)P→Px+y例6求lim=3 xy解函数(x,J)=+是初等函数，它的定义域为D=(x,V)x0,y0)。xy因D不是连通的，故D不是区域。但D,=((x,J)x>0,y>O)是区域，且D,CD，所以D是函数f(x,y)的一个定义区域。因P(1,2)ED，故lm= (.2)=号2a如果这里不引进区域D，也可用下述方法判定函数f(x,y)在点P(1,2）处是连续的：因P。是f(x,y)的定义域D的内点，故存在P的某一邻域U(P）CD，而任何邻域都是区域，所以U(P)是f(x,J)的一个定义区域，又由于f(x,y)是初等函数，因此f(x,y)在点P处连续。一般地，求limf(P),如果f(P)是初等函数，且P是f(P)的定义域的内点，则f(P)P-→P在点P。处连续，于是limf(P)=f(P)。P-PoVxy+1-1例7求limxy130/xy+1-111xy +11=lim=lim解limxy338/xy+1+133838 xy(/xy+1+1)sin(x"y)例8：求lim538 x+y2

一切多元初等函数在其定义区域内是连续的。所谓定义区域是指包含在定义域内的区 域或闭区域。 由多元初等函数的连续性，如果要求它在点 P0 处的极限，而该点又在此函数的定义区 域内，则极限值就是函数在该点的函数值，即 lim ( ) ( ) 0 0 f P f P P P = → . 例 6 求 xy x y y x + → → 2 1 lim . 解 函数 xy x y f x y + ( , ) = 是初等函数，它的定义域为 D = {(x, y) x ≠ 0, y ≠ 0}。 因 D 不是连通的，故 D 不是区域。但 {( , ) 0, 0} D1 = x y x > y > 是区域，且 D1 ⊂ D ，所 以 D 是函数 f (x, y) 的一个定义区域。因 0 1 P (1,2) ∈ D , 故 2 3 lim (1,2) 2 1 = = + → → f xy x y y x . 如果这里不引进区域 D1，也可用下述方法判定函数 f (x, y) 在点 (1,2) P0 处是连续的： 因 P0 是 f (x, y) 的定义域 D 的内点，故存在 P0 的某一邻域U(P0 ) ⊂ D ，而任何邻域都是区 域，所以 ( ) U P0 是 f (x, y) 的一个定义区域，又由于 f (x, y) 是初等函数，因此 f (x, y) 在点 P0 处连续。 一般地，求 lim ( ) 0 f P P→P ，如果 f (P) 是初等函数，且 P0 是 f (P) 的定义域的内点，则 f (P) 在点 P0 处连续，于是 lim ( ) ( ) 0 0 f P f P P P = → 。 例 7 求 xy xy y x 1 1 lim 0 0 + − → → 。 解 xy xy y x 1 1 lim 0 0 + − → → = ( 1 1) 1 1 lim 0 0 + + + − → → xy xy xy y x = 1 1 1 lim 0 0 → + + → xy y x = 2 1 。 例 8：求 2 2 2 0 0 sin( ) limx y x y → x y → +