《线性代数》课程教学课件（PPT讲稿）第四章 向量组的线性相关性 4-4 线性方程组的解的结构

线性代数敖程 第0101节三阶与三阶行列式 23:46 第四节线性方程组的解的结构 >一、齐次线性方程组解的性质 >二、基础解系及其求法 广三、非齐次线性方程组解的性质 》四、小结 第1项

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:46 第1页 一、齐次线性方程组解的性质 二、基础解系及其求法 三、非齐次线性方程组解的性质 第四节 线性方程组的解的结构 四、小结

线性代教教程 第0101节二阶与三阶行列式 2346 一、齐次线性方程组解的性质 1.解向量的概念 设有齐次线性方程组 41ix1+a12x2+.+axn=0 21x1+22x2+.+2nxm=0 (1) amlx1+am2x2++amn=0 若记 第2页

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:46 第2页 １．解向量的概念 设有齐次线性方程组        + + + = + + + = + + + = 0 0 0 1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 m m mn n n n n n a x a x a x a x a x a x a x a x a x     若记 （1） 一、齐次线性方程组解的性质

线性代数赦程 第0101节三阶与三阶行列式 23:46 11 12 A= l21 0l22 Q2n x= Aml 0m2 则上述方程组(1)可写成向量方程 Ax=0. 若x1=5Dx2=521,xn=5m1为方程Ax=0的 解，则 第3项

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:46 第3页 , a a a a a a a a a A m m mn n n               =        1 2 2 1 2 2 2 1 1 1 2 1               = xn x x x  2 1 则上述方程组（1）可写成向量方程 Ax = 0. 1 1 1 2 2 1 xn n1 若 x =  , x =  ,, =  为方程 Ax = 0 的 解，则

线性代数教程 第0101节二阶与三阶行列式 2346 x== 称为方程组()的解向量，它也就是向量方程 2)的解 第4项

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:46 第4页               = = 1 21 11 1 n x      称为方程组(1) 的解向量，它也就是向量方程 (2)的解．

线性代数敖程 第0101节三阶与三阶行列式 23:46 2.齐次线性方程组解的性质 (1)若x=5,x=52为Ax=0的解，则 x=51+52 也是A比=0的解。 证明：A51=0,A52=0 ·.A(51+52)=A51+A52=0 故x=51+52也是4x=0的解， 第5项

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:46 第5页 ２．齐次线性方程组解的性质 （1）若 x =  1 ,x =  2 为 Ax = 0 的解，则 x =  1 +  2 也是 Ax = 0 的解. 证明  A( 1 +  2 ) = A 1 + A 2 = 0  A 1 = 0, A 2 = 0 故 x 也是Ax 0的解. =  1 +  2 =

线性代教教程 第0101节二阶与三阶行列式 2346 (2)若x=5为Ax=0的解，k为实数，则 x=k5也是Ax=0的解. 证明A(k5)=k4(5)=k0=0. 证毕 由以上两个性质可知，方程组的全体解向量 所组成的集合，对于加法和数乘运算是封闭的， 因此构成一个向量空间，称此向量空间为齐次线 性方程组A化=0的解空间. 第6预

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:46 第6页 （2）若 为 的解， 为实数，则 也是 的解． x =  1 Ax = 0 k x = k 1 Ax = 0 证明 A(k ) kA( ) k0 0.  1 =  1 = = 由以上两个性质可知，方程组的全体解向量 所组成的集合，对于加法和数乘运算是封闭的， 因此构成一个向量空间，称此向量空间为齐次线 性方程组 Ax = 0 的解空间． 证毕

线性代数教程 第0101节三阶与三阶行列式 23:46 二、基础解系及其求法 1.基础解系的定义 刀1,2，7，称为齐次线性方程组4Ax=0的基础 解系，如果 ()71,72,.,7,是4x=0的一组线性无关的解； (2)Ax=0的任一解都可由71,72，7线性表 出. 第7项

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:46 第7页 解 系 如 果 称为齐次线性方程组 的基础 , 1 ,2 ,,t Ax = 0 (1) , , , 0 ; 1 2  t是Ax = 的一组线性无关的解 . (2) 0 , , , 1 2 出 Ax = 的任一解都可由   t线性表 １．基础解系的定义 二、基础解系及其求法

线性代教教程 第0101节二阶与三阶行列式 2346 如果71,2，7，为齐次线性方程组Ax=0 的一组基础解系，那么，Ax=0的通解可表示为 x=k☑1+k272+.+kn, 其中k1,k2,k,是任意常数 第8页

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:46 第8页 的一组基础解系 那么 的通解可表示为 如果 为齐次线性方程组 0 = = Ax t Ax , , 1 ,2 ,, 0 x = k11 + k22 ++ ktt , , , . 其中k1 k2  kn−r是任意常数

线性代数赦程 第0101节三阶与三阶行列式 2346 2.线性方程组基础解系的求法 设齐次线性方程组的系数矩阵为A,并不妨 设A的前r个列向量线性无关.于是A可化为 0 bu bi.n-r 1 A~ 0 bra-r 0 0 0 第9页

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:46 第9页 ２．线性方程组基础解系的求法                   − − 0 0 0 0 0 1 1 0 ~ 1 , 1 1 1,                         r r n r n r b b b b A 设齐次线性方程组的系数矩阵为 ，并不妨 设 的前 r 个列向量线性无关．于是 可化为 A A A

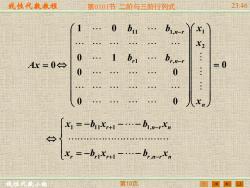
线性代数故程 第0101节二阶与三阶行列式 2346 1 0 bu bi-r 0 .1b Ax=0→ =0 . 0 ·. 。 。 0 0 x1=-b11x,+1-.-b1n-x x,=-bx41-.-b,nx。 第10页

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:46 第10页 0 0 0 0 0 0 1 1 0 2 1 1 , 1 1 1, =                                       − − n r r n r n r x x x b b b b                                 = − − − = − − −  + − + − r r r r,n r n r ,n r n x b x b x x b x b x    1 1 1 1 1 1 1 Ax = 0