《线性代数》课程教学课件（PPT讲稿）第四章 向量组的线性相关性 4-1 向量组及其线性组合

线性代教教程 第四章向量组的线性相联性 2346 第一节向量组及其线性组合 一、向量的概念及其运算 二、向量组的概念及相关定理 第1页

线性代数教程 线性代数小组 第四章 向量组的线性相关性 23:46 第1页 第一节 向量组及其线性组合 一、 向量的概念及其运算 二、 向量组的概念及相关定理

线性代数教程 第四章向量组的线性相关性 23:46 一、向量的概念及其运算 1.向量的定义 定义1n个有次序的数a,2,4.所组成的数 组称为n维向量，这n个数称为该向量的n个分量， 第个数称为第个分量. 分量全为实数的向量称为实向量， 分量全为复数的向量称为复向量， 第2项

线性代数教程 线性代数小组 第四章 向量组的线性相关性 23:46 第2页 定义1 . , , , 1 2 第 个 数 称为第 个分量 组称为 维向量，这 个数称为该向量的 个分量， 个有次序的数 所组成的数 i a i n n n n a a a i  n 分量全为复数的向量称为复向量. 分量全为实数的向量称为实向量， 一 、向量的概念及其运算 １．向量的定义

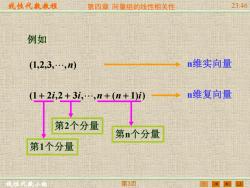
线性代数教程 第四章向量组的线性相送性 2346 例如 (1,2,3,n) n维实向量 (1+2i,2+3i,.,n+(n+1)) n维复向量 第2个分量 第n个分量 第个分量 第3页

线性代数教程 线性代数小组 第四章 向量组的线性相关性 23:46 第3页 例如 (1,2,3,  ,n) (1 + 2i,2 + 3i,  ,n + (n + 1)i) n维实向量 n维复向量 第1个分量 第n个分量 第2个分量

线性代数教程 第四章向量组的线性相关性 23:46 2.维向量的表示方法 n n维向量写成一行，称为行向量，也就是行 矩阵，通常用a,b,a,β等表示，如： a'-(a1,02,n) n维向量写成一列，称为列向量，也就是列 矩阵，通常用、b,a,B等表示，如： n a= 第4项

线性代数教程 线性代数小组 第四章 向量组的线性相关性 23:46 第4页 ( , , , ) 1 2 n T a = a a  a               = an a a a  2 1 2． 维向量的表示方法 维向量写成一行，称为行向量，也就是行 矩阵，通常用   等表示，如： T T T T a ,b , , n 维向量写成一列，称为列向量，也就是列 矩阵，通常用 a,b,, 等表示，如： n n

线性代教教程 第四章向量组的线性相送性 2346 注意 1,行向量和列向量总被看作是两个不同的 向量 2,行向量和列向量都按照矩阵的运算法则 进行运算 3,.当没有明确说明是行向量还是列向量时， 都当作列向量. 第5页

线性代数教程 线性代数小组 第四章 向量组的线性相关性 23:46 第5页 注意 １．行向量和列向量总被看作是两个不同的 向量； ２．行向量和列向量都按照矩阵的运算法则 进行运算； ３．当没有明确说明是行向量还是列向量时， 都当作列向量

线性代数教程 第四章向量组的线性相关性 2346 3.向量的运算 向量的运算按照矩阵的运算规则进行。 第6顾

线性代数教程 线性代数小组 第四章 向量组的线性相关性 23:46 第6页 ３．向量的运算 向量的运算按照矩阵的运算规则进行

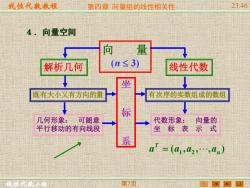
线性代教教程 第四章向量组的线性相送性 2346 4.向量空间 解析几何 (n≤3) 线性代数 坐 既有大小又有方向的量 有次序的实数组成的数组 标 几何形象：可随意 代数形象： 向量的 平行移动的有向线段 坐标表 示式 a=(a1,2,.,0n） 第7页

线性代数教程 线性代数小组 第四章 向量组的线性相关性 23:46 第7页 向 量 解析几何 (n  3) 线性代数 既有大小又有方向的量 有次序的实数组成的数组 几何形象： 可随意 平行移动的有向线段 代数形象： 向量的 坐 标 表 示 式 ( , , , ) 1 2 n T a = a a  a 坐 标 系 ４．向量空间

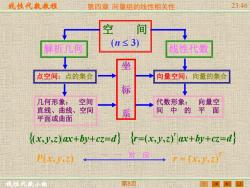
线性代数敖程 第四章向量组的线性相关性 23:46 间 解析几何 n≤3) 线性代数 坐 点空间：点的集合 向量空间：向量的集合 标 几何形象： 空间 代数形象： 向量空 直线、曲线、空间 平面或曲面 系 间中的平 面 {(x,y,z)ax+by+cz=d}r=(x,y,z)ax+by+cz=dj P) 一 对应一r=(X,山 第8项

线性代数教程 线性代数小组 第四章 向量组的线性相关性 23:46 第8页 空 间 (n  3) 解析几何 线性代数 点空间：点的集合 向量空间：向量的集合 坐 标 系 代数形象： 向量空 间 中 的 平 面 r x y z ax by cz d T =( , , ) + + = 几何形象： 空间 直线、曲线、空间 平面或曲面 (x, y,z)ax+by+cz=d P(x, y,z) r (x, y,z) T = 一 一 对 应

线性代教教程 第四章向量组的线性相送性 2346 n>3时，n维向量没有直观的几何形象 R==)R 叫做n维向量空间. ==)axta:x++ax.=b 叫做n维向量空间R"中的n-1维超平面. 第9页

线性代数教程 线性代数小组 第四章 向量组的线性相关性 23:46 第9页 R x x x xn x x xn R n T = =( 1 , 2 ,  , ) 1 , 2 ,  ,  x x x xn a x a x an xn b T  = =( 1 , 2 ,  , ) 1 1+ 2 2++ = 叫做 n 维向量空间． n  3 时， n 维向量没有直观的几何形象． 叫做 维向量空间 R 中的 维超平面． n n n − 1

线性代数敖程 第四章向量组的线性相关性 23:46 n维向量的实际意义 确定飞机的状态，需 要以下6个参数： 机身的仰角 机翼的转角 机身的水平转角 (0≤0<2π) 飞机重心在空间的位置参数Py,☑ 所以，确定飞机的状态，需用6维向量 4=x,y,z,0,Ψ，0) 第10页

线性代数教程 线性代数小组 第四章 向量组的线性相关性 23:46 第10页 确定飞机的状态，需 要以下6个参数： 飞机重心在空间的位置参数P(x,y,z) 机身的水平转角  (0    2 ) 机身的仰角 ) 2 2 (     −   机翼的转角  (−    ) 所以，确定飞机的状态，需用6维向量 a = (x, y,z,, , ) n 维向量的实际意义