《线性代数》课程教学课件（PPT讲稿）第五章 相似矩阵及二次型 第五节 二次型及其标准型

线性代数教程第0505节三次型及其标准型 2346 第五节二次型及其标准型 一、二次型及其标准形的概念 二、二次型的表示方法 三、二次型的矩阵及秩 四、化二次型为标准形 五、小结思考题 线性代数小组 第1页

线性代数教程 线性代数小组 第0505节 二次型及其标准型 23:46 第1页 第五节 二次型及其标准型 一、二次型及其标准形的概念 二、二次型的表示方法 三、二次型的矩阵及秩 四、化二次型为标准形 五、小结 思考题

线性代数教程第0505节三次型及其标准型 2346 一、二次型及其标准形的概念 定义1含有n个变量x1,x2,x的二次齐次函数 f(x2x)=auxi+axi++amxi +2012X1x2+2a13x1x3++20n-,nxn-xn 称为二次型 当a是复数时，f称为复二次型； 当，是实数时，称为实二次型 线性代数小组 第2项

线性代数教程 线性代数小组 第0505节 二次型及其标准型 23:46 第2页 一、二次型及其标准形的概念 ( ) n n n n n nn n a x x a x x a x x f x x x a x a x a x 1 2 1 2 1 3 1 3 1, 1 2 2 2 2 2 2 1 2 1 1 1 2 2 2 , , , + + + + − − = + + +    称为二次型. 定 义1 含 有n个变量x1 , x2 ,  , xn的二次齐次函数 当a 是复数时, f称为 ; ij 复二次型 当a 是实数时, f称为 . ij 实二次型

线性代数教程第0505节三次型及其标准型 23:46 只含有平方项的二次型 ∫=k+k2+.+ky房 称为二次型的标准形（或法式）. 例如 f(x,x2,x3)=2x+4x+5x3-4xy, f(x1,x2,x3)=xx2+x13+x2x 都为二次型， fx,x2,x3)=x2+4x+4x 为二次型的标准形 线性代数小组 第3页

线性代数教程 线性代数小组 第0505节 二次型及其标准型 23:46 第3页 只含有平方项的二次型 2 2 2 2 2 1 1 n n f = k y + k y ++ k y 称为二次型的标准形（或法式）． 例如 ( ) 1 3 2 3 2 2 2 1 2 3 1 f x , x , x = 2x + 4x + 5x − 4x x 都为二次型； ( ) 2 3 2 2 2 1 2 3 1 f x , x , x = x + 4x + 4x 为二次型的标准形. ( ) 1 2 3 1 2 1 3 2 3 f x , x , x = x x + x x + x x

线性代数教程第0505节一次型及其标准型 2346 二、二次型的表示方法 1.用和号表示 对二次型 f(c1,x2,xn)=411+a2x+.+mx +2012x1x2+2013x1x3+.+20m-,mxn-x 取ar=a,则2xxj=agxixj+ajixjx,于是 f=aux1+a2xx2++auxxn +L21x21+022x2+.+02mx2xn +.+0 m1XnX1+a2xnx2+.+amx} = ∑agxixj ,j= 线性代数小组 第4项

线性代数教程 线性代数小组 第0505节 二次型及其标准型 23:46 第4页 1．用和号表示 ( ) n n n n n nn n a x x a x x a x x f x x x a x a x a x 1 2 1 2 1 3 1 3 1, 1 2 2 2 2 2 2 1 2 1 1 1 2 2 2 , , , + + + + − − = + + +    对二次型 a a , 取 ji = ij 2a x x a x x a x x , 则 ij i j = ij i j + ji j i 于是 a x a x x a n x xn f 12 1 2 1 1 2 = 11 1 + ++ . , 1 a xi x j n i j =  ij = a x x a x a2n x2 xn 2 + 21 2 1 + 22 2 ++ + 2 + an1 xn x1 + an2 xn x2 ++ ann xn 二、二次型的表示方法

线性代数教程第0505节三次型及其标准型 23:46 2.用矩阵表示 f=011x1+412x1x2+.+41Xxn +021x2x1+022x2+.+02mx2xm ++anxnx1+an2xnx2++amxz =x1(411x1+412x2+.+01mxn) +x2(a21x1+422x2+.+a2nxn) ++xn(anlx+an2x2++anxn) 11x1+a12X2+.+01mx a21X1+022x2+.+2nXm =（X1)X2,Xn 。 anlx1+0n22+.+amxn 线性代数小组 笔5页

线性代数教程 线性代数小组 第0505节 二次型及其标准型 23:46 第5页 2．用矩阵表示 a x a x x a n x xn f 12 1 2 1 1 2 = 11 1 + ++ a x x a x a2n x2 xn 2 + 21 2 1 + 22 2 ++ + 2 + an1 xn x1 + an2 xn x2 ++ ann xn ( ) ( ) ( ) 1 1 2 2 2 2 1 1 2 2 2 2 1 1 1 1 1 2 2 1 n n n nn n n n n n x a x a x a x x a x a x a x x a x a x a x + + + + + + + + + = + + +                   + + + + + + + + + = n n nn n n n n n n a x a x a x a x a x a x a x a x a x x x x      1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 1 2 ( , , , )

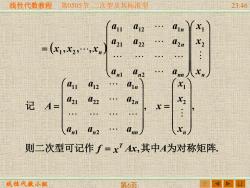
线性代数教程第0505节三次型及其标准型 2346 11 L12 Cin U21 l22 Q2n x2 =(比1，x2,xn l 2 41 012 n L21 l22 . 记 A A2n x= n 0n2 则二次型可记作f=x?Ax,其中A为对称矩阵 线性代数小组 第6页

线性代数教程 线性代数小组 第0505节 二次型及其标准型 23:46 第6页 则二次型可记作 f x Ax,其中A为对称矩阵. T = , , 2 1 1 2 2 1 2 2 2 1 1 1 2 1               =               = n n nn n n n x x x x a a a a a a a a a A         记 ( )                             = n n nn n n n n x x x a a a a a a a a a x x x          2 1 1 2 2 1 2 2 2 1 1 1 2 1 1 2 , ,

线性代数教程 第0505节三次型及其标准型 23:46 三、二次型的矩阵及秩 在二次型的矩阵表示中，任给一个二次型， 就唯一地确定一个对称矩阵；反之，任给一个对 称矩阵，也可唯一地确定一个二次型.这样，二 次型与对称矩阵之间存在一一对应的关系. 对称矩阵A叫做二次型f的矩阵； f叫做对称矩阵A的二次型； 对称矩阵4的秩叫做二次型f的秩 线性代数小组 第页

线性代数教程 线性代数小组 第0505节 二次型及其标准型 23:46 第7页 三、二次型的矩阵及秩 在二次型的矩阵表示中，任给一个二次型， 就唯一地确定一个对称矩阵；反之，任给一个对 称矩阵，也可唯一地确定一个二次型．这样，二 次型与对称矩阵之间存在一一对应的关系． 对称矩阵A叫做二次型 f 的矩阵; f 叫做对称矩阵A的二次型; 对称矩阵A的秩叫做二次型 f 的 秩

线性代数教程第0505节三次型及其标准型 2346 例1写出二次型 f=x2+2x2-3x3+4xx2-6x2x3 的矩阵 解01=1,02=2,03=-3， 02=021=2,03=031=0, 023=032=-3. 2 .A= 2 2 0 -3-3 线性代数小组 第8项

线性代数教程 线性代数小组 第0505节 二次型及其标准型 23:46 第8页 解 a 1, a 2, a 3, 11 = 22 = 33 = − a a 2, 12 = 21 = a a 0, 13 = 31 = a a 3. 23 = 32 = − . 0 3 3 2 2 3 1 2 0           − −  A = − . 2 3 4 6 1 2 2 3 2 3 2 2 2 1 的矩阵 写出二次型 f = x + x − x + x x − x x 例１

线性代数教程第0505节三次型吸其标准型 23:46 四、化二次型为标准形 对于二次型，我们讨论的主要问题是：寻求 可逆的线性变换，将二次型化为标准形. 设 x1=cuy1+C12y2++cinyn2 X2=C21y1+C22y2++c2nyn? xn =cnly+en2y2++Cmyn 记C=(c),则上述可逆线性变换可记作 x=Cy 线性代数小组 第9页

线性代数教程 线性代数小组 第0505节 二次型及其标准型 23:46 第9页        = + + + = + + + = + + + n n n nn n n n n n x c y c y c y x c y c y c y x c y c y c y     1 1 2 2 2 2 1 1 2 2 2 2 1 1 1 1 1 2 2 1 , , 设 四、化二次型为标准形 对于二次型，我们讨论的主要问题是：寻求 可逆的线性变换，将二次型化为标准形． C (c ), 记 = ij 则上述可逆线性变换可 记作 x = Cy

线性代数教程第0505节三次型及其标谁型 2346 将其代入∫=x'Ax,有 f=xTAx=(Cy)A(Cy)=y"(CZAC)y. 定理I任给可逆矩阵C,令B=CTAC,如果A为对称 矩阵，则B也为对称矩阵且R(B)-R(A) 证明A为对称矩阵即有A=A',于是 BT=(CTAC)=CTATC=CTAC=B, 即B为对称矩阵 B=CT AC,.R(B)<R(AC)3 R(A), 又：A=(CI）'BC-1,R(4)sRBC)sR(B) .R(A)=R(B). 线性代数小组 第10页

线性代数教程 线性代数小组 第0505节 二次型及其标准型 23:46 第10页 f x Ax T = 证明 A为对称矩阵,即有A = A T ,于是 ( ) T T T B = C AC 将其代入 f = x T Ax,有 y (C AC)y. T T (Cy) A(Cy) = T = , , ( ) ( ). 1 , , B R B R A C B C AC A T = = 矩 阵 则 也为对称矩阵且 定 理 任给可逆矩阵 令 如 果 为对称 C A C T T = C AC B, T = = B C AC, T  =  R(B)  R(AC)  R(A), ( ) , 1 1 − − A = C BC 又  T ( ) ( ) ( ). 1  R A  R BC  R B −  R(A) = R(B). 即 B 为对称矩阵