《线性代数》课程教学课件（PPT讲稿）第三章 矩阵的初等变换与线性方程组 3-1 矩阵的初等变换

线性代教敖程 第三章矩阵的初等变换与线性方程组 23:45 第一节 矩阵的初等变换 一、 消元法解线性方程组 二、矩阵的初等变换 三、小结 第1项

线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第1页 第一节 矩阵的初等变换 一、消元法解线性方程组 三、小结 二、矩阵的初等变换

线性代载教程 第三章矩阵的初等变换与线性方程组 2345 本章先讨论矩阵的初等变换，建立矩阵的 秩的概念，并提出求秩的有效方法.再利用矩阵 的秩反过来研究齐次线性方程组有非零解的充分 必要条件和非齐次线性方程组有解的充分必要条 件，并介绍用初等变换解线性方程组的方法，内 容丰富，难度较大 第2页 U

线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第2页 本章先讨论矩阵的初等变换，建立矩阵的 秩的概念,并提出求秩的有效方法．再利用矩阵 的秩反过来研究齐次线性方程组有非零解的充分 必要条件和非齐次线性方程组有解的充分必要条 件，并介绍用初等变换解线性方程组的方法．内 容丰富，难度较大

线性代数教程 第三章矩阵的初等变换与线性方程组 23:45 一、消元法解线性方程组 分析：用消元法解下列方程组的过程 引例求解线性方程组 2x1-x2-x3+x4=2, x1+x2-2x3+x4=4, 4x1-6x2+2x3-2x4=4,3÷2 (0 3x1+6x2-9x3+7x4=9,④ 第3项

线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第3页 引例 (1) 一、消元法解线性方程组 求解线性方程组        + − + = − + − = + − + = − − + = 3 6 9 7 9, 4 6 2 2 4, 2 4, 2 2, 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x x x x x 1 3 4 2 分析：用消元法解下列方程组的过程．  2

线性代教教程 第三章矩阵的初等变换与线性方程组 2345 解 十x223十1-4与 ①K→② 2x1-2-x3+x4=2, ( (B) 3÷2 2x1-3x2+x3-x4=2, 3x1+6x2-9x3+7x1=9,④ ©+x2-2x3+x4=4, ① ②-3 3-2① 2x22x3+2x-0, (B2) ④-3D 5x2+5x3-3x4=-6, 个 3x2-3x3+4x4=-3, 第4项

线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第4页 解 ( ) (1) B1 ( ) B2   2 1 3 2        + − + = − + − = − − + = + − + = 3 6 9 7 9, 2 3 2, 2 2, 2 4, 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x x x x x 1 3 4 2 − 2 1 2 − 3 3 4 − 3 1        − + = − − + − = − − + = + − + = 3 3 4 3, 5 5 3 6, 2 2 2 0, 2 4, 2 3 4 2 3 4 2 3 4 1 2 3 4 x x x x x x x x x x x x x 1 3 4 2

线性代数敖程 第三章矩阵的初等变换与线性方程组 23:45 2 x1+x2-2x3+x4=4, 2 2-x3+x4=0, (B3) 3+5② 2x4=-6, ④-32 x4=3, x1+x2-2x3+x4=4, ① ③←→④ 3+x4=0, ② (B4) ④-23 9=-3, 3 0=0, ④ 用“回代”的方法求出解： 第5项

线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第5页 ( ) B3 ( ) B4        = − = − − + = + − + = 3, 2 6, 0, 2 4, 4 4 2 3 4 1 2 3 4 x x x x x x x x x 1 3 4 2 + 5 2 2 1  3 4 − 3 2 2        = = − − + = + − + = 0 0, 3, 0, 2 4, 4 2 3 4 1 2 3 4 x x x x x x x x 1 3 4 3  2 4 − 2 4 3 用“回代”的方法求出解：

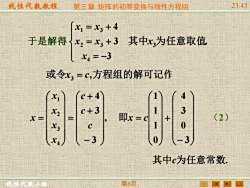
线性代教赦程 第三章矩阵的初等变换与线性方程组 2345 x1=x3+4 于是解得x,-=x+3其中x,为任意取值 x4=-3 或令x,=c,方程组的解可记作 c+4 c+3 x= 即x=d (2) -3 其中c为任意常数： 第6卖

线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第6页 于是解得      = − = + = + 3 3 4 4 2 3 1 3 x x x x x . 其中x3为任意取值 或令x3 = c,方程组的解可记作 , 3 3 4 4 3 2 1               − + + =               = c c c x x x x x 其中c为任意常数.               − +               = 3 0 3 4 0 1 1 1 即x c （2）

线性代数故程 第三章矩阵的初等变换与线性方程组 23:45 小结： 1.上述解方程组的方法称为消元 法·始终把方程组看作一个整体变形，用到如 下三种变换 (1)交换方程次序； (①与D相互替换) (2)以不等于0的数乘某个方程； (以①×k替换①) (3)一个方程加上另一个方程的k倍. (以①+k①替换①) 第7项

线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第7页 小结： 1．上述解方程组的方法称为消元 法．2．始终把方程组看作一个整体变形，用到如 下三种变换 （1）交换方程次序； （2）以不等于０的数乘某个方程； （3）一个方程加上另一个方程的k倍． （ i 与 j 相互替换） （以 i  k 替换 i ） （以 i + k j 替换 i ）

线性代教教程 第三章矩阵的初等变换与线性方程组 2345 3.上述三种变换都是可逆的. 若429(B.则(B)I2 (A; 若(4DXK(B.则(B)D÷k(A; 若A)①+k0(B,则(B)2-k①(4 由于三种变换都是可逆的，所以变换前的 方程组与变换后的方程组是同解的.故这三种 变换是同解变换. 第8页

线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第8页 3．上述三种变换都是可逆的． 由于三种变换都是可逆的，所以变换前的 方程组与变换后的方程组是同解的．故这三种 变换是同解变换． i j 若(A) (B),  则(B) (A); i  j + k 若(A) (B), i j 若(A) (B), i  k 则(B) (A); i  k 则(B) (A). i − k j

线性代数教程 第三章矩阵的初等变换与线性方程组 2345 因为在上述变换过程中，仅仅只对方程组 系数和常数进行运算，未知量并未参与运 算 若记 -1 -112 B=(Ab)= 2 1 -2 14 -6 2 -2 4 3 6 9 79 则对方程组的变换完全可以转换为对矩阵B(方 程组(1)的增广矩阵)的变换. 第9页

线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第9页 因为在上述变换过程中，仅仅只对方程组 的系数和常数进行运算，未知量并未参与运 算．若记               − − − − − − = = 3 6 9 7 9 4 6 2 2 4 1 1 2 1 4 2 1 1 1 2 B (Ab) 则对方程组的变换完全可以转换为对矩阵B(方 程组（1）的增广矩阵）的变换．

线性代教故程第三章矩阵的初等变换与线性方程组 2345 二、矩阵的初等变换 定义1下面三种变换称为矩阵的初等行变换： ()对调两行（对调，两行，记作，→)； (2)以数k≠0乘以某一行的所有元素 (第i行乘k,记作r×k) 3)把某一行所有元素的k倍加到另一行 对应的元素上去（第行的k倍加到第行上 记作r:+kr) 第10页

线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第10页 定义1 下面三种变换称为矩阵的初等行变换: (1)对调两行（对调i, j两行,记作ri  rj）； (2)以 数 k  0 乘以某一行的所有元素; （第 i 行乘 k,记作 ri  k） ( ) . 3 记 作 ） 对应的元素上去（第 行 的 倍加到第 行 上 把某一行所有元素的 倍加到另一行 i krj r j k i k + 二、矩阵的初等变换