《线性代数》课程教学课件（PPT讲稿）第二章 矩阵及其运算 2-2 矩阵的运算

线性代教教程 22矩阵的运算 2345 一、矩阵的加法 1、定义 设有两个m×n矩阵A-(a,)B-b,)那末矩阵 A与B的和记作A+B,规定为 a+b.( r2+br2 ar+b A十B= a1+b21 .+b2 .an+b,. am+bm a2+bm2 .amn+bnm 说明只有当两个矩阵是同型矩阵时，才能进 行加法运算， 小组 第1项

线性代数教程 线性代数小组 2-2 矩阵的运算 23:45 第1页 １、定义             + + + + + + + + + + = m m m m m n m n n n n n a b a b a b a b a b a b a b a b a b A B        1 1 2 2 21 21 22 22 2 2 11 11 12 12 1 1 一、矩阵的加法 设有两个 矩阵 那末矩阵 与 的和记作 ，规定为 mn A (a ), B (b ), = ij = ij A B A+ B 说明 只有当两个矩阵是同型矩阵时，才能进 行加法运算

线性代数教程 22矩阵的运算 2345 2、矩阵加法的运算规律 (1)A+B=B+A; (2)(A+B)+C=A+(B+C) -au -L2 (3)-A= -2 -02 (a, 一L 称为矩阵A的负矩阵。 (4)A+(-A)=0,A-B=A+(-B) 第2项

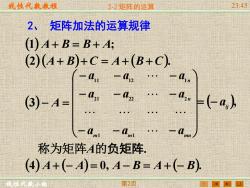
线性代数教程 线性代数小组 2-2 矩阵的运算 23:45 第2页 2、 矩阵加法的运算规律 (1) A+ B = B + A; (2)(A+ B)+ C = A+ (B + C). ( )             − − − − − − − − − − = m m m n n n a a a a a a a a a A        1 1 21 22 2 11 12 1 3 (4) A+ (− A) = 0, A− B = A+ (− B). ( ), = − aij 称为矩阵A的负矩阵

线性代数故程 22矩阵的运算 2345 二、数与矩阵相乘 1、定义 数几与矩阵4的乘积记作24或A2,规定为 Mae 2 2A=A入= 22i M Azn 与行列 式的乘 xa Aa 法不同 第3页

线性代数教程 线性代数小组 2-2 矩阵的运算 23:45 第3页 1、定义 . 1 1 21 22 2 11 12 1             = = m m m n n n a a a a a a a a a A A                   二、数与矩阵相乘 数与矩阵A的乘积记作A或A,规定为 与行列 式的乘 法不同

线性代数枚程 2:2矩阵的运算 2345 2、数乘矩阵的运算规律 (设A、B为m×n矩阵，九，u为数) )(2)A=(4)月 (2)(2+4)A=4+4 3)2(A+B)=2A+1B. 矩阵相加与数乘矩阵合起来，统称为矩阵的线 性运算。 第4项

线性代数教程 线性代数小组 2-2 矩阵的运算 23:45 第4页 (1)()A = (A); (2)( + )A = A+ A; (3) (A+ B) = A+ B. 2、数乘矩阵的运算规律 矩阵相加与数乘矩阵合起来,统称为矩阵的线 性运算. （设 A、B 为 mn 矩阵，  , 为数）

线性代数教程 22矩阵的运算 2345 三、矩阵与矩阵相乘 1、定义 设A=(4,是一个m×s矩阵，B=(bn)是一 个s×矩阵，那末规定矩阵A与矩阵B的乘 积是一个m×n矩阵C=(cn)其中 C,=ab,+ab,+.+a.b,=∑abg (i=1,2,.m;j=1,2,.,n, 有何 规律 并把此乘积记作C=AB. 第5页

线性代数教程 线性代数小组 2-2 矩阵的运算 23:45 第5页 １、定义 = = + + + = s k ij ai b j ai b j ai sbsj ai kbkj c 1 1 1 2 2  (i = 1,2, m; j = 1,2,  ,n), 并把此乘积记作 C = AB. 三、矩阵与矩阵相乘 设 是一个 矩阵， 是一 个 矩阵，那末规定矩阵 与矩阵 的乘 积是一个 矩阵 ，其中 ( ) A = aij m  s ( ) B = bij s  n m n ( )ij C = c A B 有何 规律

线性代数赦程 2:2矩阵的运算 23:45 例1 c6( 2×2 例2设 0 3 4 0 -12 A=-1 1 3 0 B= 05-14 3 -1 2 AB=? 第6顾

线性代数教程 线性代数小组 2-2 矩阵的运算 23:45 第6页 例１ 2 2 3 6 2 2 2 4 1 2 2 4         − −       − − C = 22       = −16− 32 8 16 设           − − − = 0 5 1 4 1 1 3 0 1 0 1 2 A             − − = 1 2 1 3 1 1 1 2 1 0 3 4 B 例2 ? AB = ?

线性代数故程 22矩阵的运算 2345 两个矩阵满足什么条件可以相乘？ 只有当第一个矩阵的列数等于第二个矩阵 的行数时，两个矩阵才能相乘 123 例如 3 2 不存在 58 23) 321 =(1×3+2×2+3×1)=(10) 第7页

线性代数教程 线性代数小组 2-2 矩阵的运算 23:45 第7页 只有当第一个矩阵的列数等于第二个矩阵 的行数时，两个矩阵才能相乘.                 6 0 1 1 6 8 5 8 9 3 2 1 1 2 3 例如 ( )           1 2 3 1 2 3 = (1 3 + 2 2 + 31) = (10). 不存在. ？两个矩阵满足什么条件可以相乘？

线性代数教程 22矩阵的运算 2345 2、矩阵乘法的运算规律 I)(AB)C=A(BC)方 (2)A(B+C)=AB+AC,(B+C)A=BA+CA; (3)(AB)=(24)B=A(B)(其中2为数)； ()AE=EA=A; (2E)An=24=A(2E.) 何有珠婴单香不 k个 m,k为正整数 第8项

线性代数教程 线性代数小组 2-2 矩阵的运算 23:45 第8页 ２、矩阵乘法的运算规律 (1)(AB)C = A(BC); (2) A(B + C) = AB + AC,(B + C)A = BA+ CA; (3) (AB) = (A)B = A(B) （其中  为数）; (4) AE = EA = A; 若A是 阶矩阵，则 为A的 次幂，即 并且 (5) n k A k   k个 k A = A A A , m k m k A A A + = ( ) . mk m k A = A m,k ( ) ( ) E n A n = A n = A n E n 为正整数

线性代教教程 22矩阵的运算 2345 矩阵乘法满足交换律吗？ 04日1）-D -0a-3》 AB≠BA. A≠0，B≠0，AB=0 发现什么 注意 矩阵不满足交换律，即： AB≠BA,(AB≠AB. 第9页

线性代数教程 线性代数小组 2-2 矩阵的运算 23:45 第9页 注意 矩阵不满足交换律，即： AB  BA, ( ) . k k k AB  A B 例 设       − − = 1 1 1 1 A       − − = 1 1 1 1 B 则 , 0 0 0 0       AB = , 2 2 2 2       − − BA = AB  BA. 矩阵乘法满足交换律吗？ A  0,B  0, AB = 0 发现什么

线性代数赦程 22矩阵的运算 2345 但也有例外，比如设 4=6 则有 AB- 2 2） →AB=BA. 第10页

线性代数教程 线性代数小组 2-2 矩阵的运算 23:45 第10页 但也有例外，比如设 , 0 2 2 0       A = , 1 1 1 1       − − B = 则有 , 2 2 2 2       − − AB =       − − = 2 2 2 2 BA  AB = BA