《线性代数》课程教学课件（PPT讲稿）第二章 矩阵及其运算 2-3 逆矩阵

线性代数敖程 第0101节三阶与三阶行列式 2345 第三节逆矩阵 一、概念的引入 二、逆矩阵的概念和性质 三、逆矩阵求法 四、小结 第1项

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第1页 第三节 逆矩阵 一、概念的引入 四、小结 二、逆矩阵的概念和性质 三、逆矩阵求法

线性代教故程 第0101节二阶与三阶行列式 2345 一、概念的引入 在数的运算中，当数a≠0时，有 aa=aa=1, 推广到炬阵 中 其中a1=1为a的倒数，（或称a的逆）； 在矩阵的运算中，单位阵E相当于数的乘法运算中 的1，那么，对于矩阵A如果存在一个矩阵4， 使得AAI=AA=E, 则矩阵A称为A的可逆矩阵或逆阵 第2项

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第2页 1, 1 1 = = − − aa a a , 1 1 AA = A A = E − − 则矩阵 称为 A 的可逆矩阵或逆阵. −1 A 一、概念的引入 在数的运算中，当数 a  0 时，有 a a 1 1 = 其中 − 为 a 的倒数，（或称 a 的逆）； 在矩阵的运算中，单位阵 E 相当于数的乘法运算中 的1，那么，对于矩阵 A ， −1 如果存在一个矩阵 A , 使得 推广到矩阵 中

线性代数教程 第0101节二阶与三阶行列式 23:45 二、逆矩阵的概念和性质 定义对于n阶矩阵A,如果有一个n阶矩阵B, 使得AB=BA=E, 则说矩阵A是可逆的，并把矩阵B称为A的逆矩阵 A的逆矩阵记作A 日4-母 ,AB=BA=E,所以B是A的一个逆矩阵 第3项

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第3页 二、逆矩阵的概念和性质 定义 对于 阶矩阵 ，如果有一个 阶矩阵 , 则说矩阵 是可逆的，并把矩阵 称为 的逆矩阵. n A B AB = BA = E, B A n A 使得 . −1 A的逆矩阵记作A 例 设 , 1 2 1 2 1 2 1 2 , 1 1 1 1       −  =      − A = B AB = BA = E, 所以B是A的一个逆矩阵

线性代教教程 第0101节二阶与三阶行列式 2345 说明若是可逆矩阵，则A的逆矩阵是唯一的， 若设B和C是A的可逆矩阵，则有 AB=BA-E,AC=CA=E, 可得B=EB=(CA)B=C(AB)=CE=C. 所以A的逆矩阵是唯一的，即 B=C=4. 证明唯一的方法 ；单位矩阵的分 解 第4项

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第4页 说明 若 A 是可逆矩阵，则 A 的逆矩阵是唯一的. B 若设 C A B 和C 是A 的可逆矩阵，则有 AB = BA = E,AC = CA = E, 可得 B = EB = (CA)B = C(AB) = CE = C. 所以 A 的逆矩阵是唯一的,即 . −1 B = C = A 证明唯一的方法 ；单位矩阵E的分 解

线性代数敖程 第0101节三阶与三阶行列式 2345 定理1矩阵A可逆的充要条件是A≠0，且 其中4为矩阵4的伴随矩阵 证明若A可逆，即有A使AA=E. AA=E=1所以A≠0 第5项

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第5页 定理1 矩阵 可逆的充要条件是 ，且 , −1 1  = A A A A A  0 证明 若 A 可逆， . 1 1 A AA = E 即有 − 使 − 1 1  = = − A A E A  0 其中A 为矩阵A的伴随矩阵.  所以

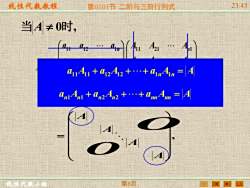
线性代教教程 第0101节三阶与三阶行列式 2345 当A≠0时， 411Al+a242+.+amAn=4 am An an2An2++am Am A 第6顾

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第6页 当A  0时,                             =  n n nn n n n n nn n n A A A A A A A A A a a a a a a a a a AA               1 2 1 2 2 2 2 1 1 2 1 1 1 2 2 1 2 2 2 1 1 1 2 1 a11A11 + a12A12 ++ a1nA1n = A an1An1 + an2An2 ++ annAnn = A ,               = A A A A O O 

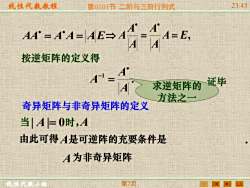
线性代数敖程 第0101节二阶与三阶行列式 23:45 AA-AA-AE-A4-4A-E 按逆矩阵的定义得 A 求逆矩阵的 证毕 方法之一 奇异矩阵与非奇异矩阵的定义 当|A=0时，A 由此可得A是可逆阵的充要条件是 A为非奇异矩阵 第7项

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第7页 AA = A A = AE   A E, A A A A  A = =   . 1 A A A  − = 按逆矩阵的定义得 证毕 奇异矩阵与非奇异矩阵的定义 . 为非奇异矩阵 由此可得 是可逆阵的充要条件是 A A 当 | A|= 0 时， A 求逆矩阵的 方法之一

线性代数故程 第0101节二阶与三阶行列式 2345 推论若AB=E(或BA=E),则B=AI 证明 AB=E-1,A≠0， 因而存在，于是 B=EB=（A'A)B=A'(AB) -E-N 逆矩阵的运算性质 (1)若A可逆，则A亦可逆，且(4)'=A 第8页

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第8页 A  B = E = 1,  A  0, , 1 因而 存在 − A 于是 B = EB (A A)B −1 = A (AB) −1 = A E −1 = . −1 = A ( ), . −1 推论 若AB = E 或BA = E 则B = A 证明 逆矩阵的运算性质 , , ( ) . 1 1 1 A A A = A - 若 可逆 则 - 亦可逆 且 - (1)

线性代数教程 第0101节三阶与三阶行列式 23:45 (2)若A可逆，数入≠0，则24可逆，且 -之知 (3)若A,B为同阶方阵且均可逆，则AB亦可逆，且 (A B)=BA 证明 (AB)BA-)=A(BB-)A =AEA-=AA=E, .(AB)=BA-. 第9页

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第9页 ( ) 2 若A可逆,数  0,则A可逆,且 ( )( ) ( ) −1 −1 −1 −1 AB B A = A BB A −1 = AEA , 1 = AA = E − ( ) . −1 −1 −1  AB = B A 证明 ( ) = −1 A B B −1 −1 A ( ) . −1 1 −1 A = A   (3)若 A,B 为同阶方阵且均可逆 , 则 AB 亦可逆 ,且

线性代教教程 第0101节二阶与三阶行列式 2345 推广（A,A，.An)1-Am.·A2·A (4)若A何逆，则4亦可逆，()()月 证明·A(Ay=(4A=E=E, .(4=(4y 另外，当A≠0时，定义 A=E,A=(4).(为正整数) 第10页

线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第10页 ( ) ( ) T T T A A A A −1 −1  = T = E = E, ( ) ( ) . 1 1 T T A A − −  = , ( ) . , 0 , 0 1 k k A E A A A − − = = 另外 当  时 定义 证明 (k为正整数) ( ) ( ) 推广 1 1 2 ( , , ) − A A A m 1 1 1 2 −1 − − = A m    A  A 若 可逆,则 亦可逆 ,且 A = A . T −1 −1 T T （4） A A