《线性代数》课程教学课件（PPT讲稿）第一章 行列式 1-3 n阶行列式

线性代数敖程 第一章阶行列式 第三节阶行列式 一、概念的引入 二、n阶行列式的定义 三、小结、思考题

线性代数教程 线性代数小组 第一章 n阶行列式 第三 节 n阶行列式 一、概念的引入 三、小结、思考题 二、n 阶行列式的定义

线性代数教程 第一章阶行列式 一、概念的引入 三阶行列式 02 013 D=L21 L23=n0223+42,031+0321032 031 3243-013022031-01023032-012021033 说明 (1) 三阶行列式共有6项，即3项 (2)每项都是位于不同行不同列的三个元素的 乘积

线性代数教程 线性代数小组 第一章 n阶行列式 一、概念的引入 三阶行列式 31 32 33 21 22 23 11 12 13 a a a a a a a a a D = 11 22 33 12 23 31 13 21 32 = a a a + a a a + a a a 13 22 31 11 23 32 12 21 33 − a a a − a a a − a a a 说明 （1）三阶行列式共有 6 项，即 3! 项． （2）每项都是位于不同行不同列的三个元素的 乘积．

线性代数敖程 第一章阶行列式 (3)每项的正负号都取决于位于不同行不同列 的三个元素的下标排列. 例如4,442 列标排列的逆序数为 t312)=1+1=2,偶排列+正号 4L2 列标排列的逆序数为 t132)=1+0=1, 奇排列一负号， 411 012 413 22 023 (-1y aipazmasps a 32 33

线性代数教程 线性代数小组 第一章 n阶行列式 （3）每项的正负号都取决于位于不同行不同列 的三个元素的下标排列． 例如 13 21 32 a a a 列标排列的逆序数为 t(312) = 1+1 = 2, 11 23 32 a a a 列标排列的逆序数为 t(132) = 1+ 0 = 1, 偶排列 奇排列 + 正号 −负号, ( 1) . 1 1 2 2 3 3 3 1 3 2 3 3 2 1 2 2 2 3 1 1 1 2 1 3  =  − p p p t a a a a a a a a a a a a

线性代数教程 第一章阶行列式 二、n阶行列式的定义 定义由n2个数组成的n阶行列式等于所有 取自不同行不同列的n个元素的乘积 的代数和 ∑（-l'41n42p,.am. 41 012 记作D= 021 l22 .02n Anl n2.m 简记作de(a,).数a,称为行列式det(a,)的元素

线性代数教程 线性代数小组 第一章 n阶行列式 二、n阶行列式的定义 n n nn n n p p np t a a a a a a a a a D a a a n n n n        1 2 2 1 2 2 2 1 1 1 2 1 1 2 2 ( 1) . 1 2 =  − 记 作 的代数和 取自不同行不同列的 个元素的乘积 定义 由 个数组成的 阶行列式等于所有 det( ). 简记作 aij 数 aij 称为行列式det(aij)的元素．

线性代数敖程 第一章阶行列式 其中pP2·pn为自然数1,2，n的一个排列， t为这个排列的逆序数. 011412.01 D- 021022.02n 0nlan2.am =∑(-loa4nap PiP2Pn

线性代数教程 线性代数小组 第一章 n阶行列式 为这个排列的逆序数． 其 中 为自然数 ， ， 的一个排列， t p1 p2pn 1 2  n ( ) ( ) n n n p p np p p p t p p p n n nn n n a a a a a a a a a a a a D        1 2 1 2 1 2 1 2 1 2 2 1 2 2 2 1 1 1 2 1 =  − 1 =

线性代教教程 第一章阶行列式 说明 1、行列式是一种特定的算式，它是根据求解方 程个数和未知量个数相同的一次方程组的需要而 定义的； 2、n阶行列式是n.项的代数和； 3、n阶行列式的每项都是位于不同行、不同 列n个元素的乘积； 4、一阶行列式@=4不要与绝对值记号相混淆； 5、 凸p,2p,ap.的符号为(-1

线性代数教程 线性代数小组 第一章 n阶行列式 说明 1、行列式是一种特定的算式，它是根据求解方 程个数和未知量个数相同的一次方程组的需要而 定义的; 2、 n 阶行列式是 n! 项的代数和; 3、 阶行列式的每项都是位于不同行、不同 列 个元素的乘积; n n 4、 一阶行列式 a = a 不要与绝对值记号相混淆; 5、 a1 p1 a2 p2 anpn 的符号为 ( 1) . t −

线性代数敖程 第一章阶行列式 例1计算对角行列式 8 8 3 0200 1000 解分析 展开式中项的一般形式是凸n,2p,p,4n 若p1≠4→4=0，所以P只能等于4， 从而这个项为零，同理可得P2=3,P=2,P4=1

线性代数教程 线性代数小组 第一章 n阶行列式 例1 计算对角行列式 4 0 0 0 0 3 0 0 0 0 2 0 0 0 0 1 分析 展开式中项的一般形式是 1 p1 2 p2 3 p3 4 p4 a a a a 若 p1  4 0, 1 1  a p = 从而这个项为零， 所以 1 只能等于 , p 4 同理可得 p2 = 3, p3 = 2, p4 = 1 解

线性代数教程 第一章阶行列式 即行列式中不为零的项为0140230201。 0 0 0 02 0 .3 0 =(-14601.234=24. 0 011 12 din 例2计算上三角行列式 0( 22 .02n 。 00 Ann

线性代数教程 线性代数小组 第一章 n阶行列式 4 0 0 0 0 3 0 0 0 0 2 0 0 0 0 1 ( ) ( ) 1 1 2 3 4 4321 = −    t = 24. 即行列式中不为零的项为 a a a a . 14 23 32 41 例2 计算上三角行列式 nn n n a a a a a a     0 0 0 22 2 11 12 1

线性代数赦程 第一章阶行列式 解分析 展开式中项的一般形式是 a1n凸2p2.am. pm=n,Pm-1=n-1,Pm-3=n-3,p2=2,P1=1, 所以不为零的项只有41220m 41201n 02. 02n =(（-0aa,.an 00 =0122.0n

线性代数教程 线性代数小组 第一章 n阶行列式 分析 展开式中项的一般形式是 . 1 p1 2 p2 npn a a a p n, n = 1, pn−1 = n − 3, 2, 1, pn−3 = n −  p2 = p1 = 所以不为零的项只有 . 11 22 nn a a a nn n n a a a a a a     0 0 0 22 2 11 12 1  ( ) ( ) nn t n a a a  11 22 12 = −1 . 11 22 nn = a a a 解

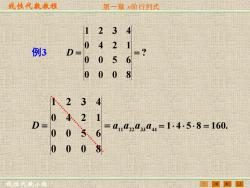
线性代教教程 第一章阶行列式 1 234 0 4 例3 21 D 0 0 5 6 ≈？ 0008 1.234 04、.21 D= 0036 =01420304=1.4.5.8=160. 000 8

线性代数教程 线性代数小组 第一章 n阶行列式 例3 ? 0 0 0 8 0 0 5 6 0 4 2 1 1 2 3 4 D = = 11 22 33 44 0 0 0 8 0 0 5 6 0 4 2 1 1 2 3 4 D = = a a a a = 1 4  5  8 = 160