《线性代数》课程教学资源（PPT课件）第四章 向量组及其线性组合 4.4 向量空间

第四节向量空间 殇性代数 内蒙古科技大学数理生学院

第四节 向量空间 内蒙古科技大学数理生学院

一、向量空间的概念 定义1设V为n维向量的集合，如果集合非空， 且集合V对于加法及乘数两种运算封闭，那么就称 集合V为向量空间. 说明 1.集合V对于加法及乘数两种运算封闭指 若a∈V,B∈V,则a+B∈V; 若a∈V,∈R,则∈V, 2.n维向量的集合是一个向量空间，记作R

说明 若 V,  R, 则  V. 2．n 维向量的集合是一个向量空间,记作 . n R 若 V, V, 则 +  V; 一、向量空间的概念 定义1 设 为 维向量的集合，如果集合 非空， 且集合 对于加法及乘数两种运算封闭，那么就称 集合 为向量空间． n V V V V 1．集合 V 对于加法及乘数两种运算封闭指

向量空间的几何意义 ●由于向量的概念具有几何性质，向量的几何通 常叫向量空间。 ●向量空间主要有两种： (1)由V中的一个向量张成的空间（如：由特 征向量张成的空间等) (2)由齐次线性方程组的解集组成的子空间 ● 由向量组{a,a,}张成的向量空间平面S的例子。 S=Spanta,a={x a +xaz x,x2 E R)

向量空间的几何意义 ⚫ 由向量组 张成的向量空间平面S的例子。 ⚫ 由于向量的概念具有几何性质，向量的几何通 常叫向量空间。 ⚫ 向量空间主要有两种： (1) 由V中的一个向量张成的空间（如：由特 征向量张成的空间等） (2) 由齐次线性方程组的解集组成的子空间 { , } { | , } S = Span a1 a2 = x1 a1 + x2 a2 x1 x2 R { , } a1 a2

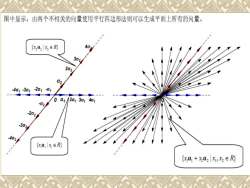
图中显示，由两个不相关的向量使用平行四边形法则可以生成平面上所有的向量。 (xu x ER) 3d2 2a2 0a1/2a13a14 02A 2d1 xaxER) {4+02x,2∈R

例13维向量的全体R3,是一个向量空间 因为任意两个3维向量之和仍然是3维向量，数 乘3维向量仍然是3维向量，它们都属于3. 类似地，n维向量的全体R",也是一个向量空 间

3 , . 例1 维向量的全体R 3 是一个向量空间 3 3 . 3 3 , 3 乘 维向量仍然是 维向量，它们都属于R 因为任意两个 维向量之和仍然是 维向量 数  . 间 类似地，n维向量的全体R n，也是一个向量空

例2判别下列集合是否为向量空间. ==0,x2,x2,R 解V是向量空间. 因为对于V的任意两个元素 a=(0,2,0n）,B=(0,b2,bn）ey, 有a+B=(0,a2+b2,n+bny∈y a=(0,2,.,nn）'eY

例2 判别下列集合是否为向量空间. V x ( x x ) x xn R T 1 = = 0, 2 ,  , n 2 ,  ,  解 V 是向量空间 . 1 因为对于V1的任意两个元素 ( ) ( ) T n T  = 0,a2 ,  ,an ,  = 0,b2 ,  ,b V ,  1 ( ) 2 2 1 0,a b , ,a b V T 有  +  = +  n + n  (0, , , ) . a2 a V1 T  =    n 

例3判别下列集合是否为向量空间。 2={x=(1,x2,xnx2,.,xn∈R 解V,不是向量空间， 因为若a=(1,2,an）YeV2, 则2a=(2,2a2,2an了eV2

例3 判别下列集合是否为向量空间. V x ( x x ) x xn R T 2 = = 1, 2 ,  , n 2 ,  ,  解 2 (2,2 , ,2 ) . a2 a V2 T 则  =  n  V 不是向量空间 . 2 (1, , , ) , 2 V2 a a T 因为若 =  n 

例4设a,b为两个已知的n维向量，集合 V={x=M+b2,4∈R 试判断集合是否为向量空间. 解V是一个向量空间因为若1=2M+山b x2=九2a+42b,则有 x1+x2=(21+2)M+(41+2)b∈V, k1=(k2)a+(k4)b∈V. 这个向量空间称为由向量4，b所生成的向量空 间

例 4 设a,b为两个已知的n维向量，集合 V = x = a + b,  R 试判断集合是否为向量空间. 解 V是一个向量空间.因为若x1 = 1 a + 1 b x2 = 2a +  2b， 则有 ( ) ( ) , x1 + x2 = 1 + 2 a + 1 +  2 b V ( ) ( ) . kx1 = k1 a + k1 bV . , 间 这个向量空间称为由向量a b所生成的向量空

般地，由向量组41,42，1m所生成的向量空 间为 V={c=元1a1+22+.+n0m21,2,2m∈R 例5 设向量组a1,.,am与向量组b1,.,b,等价， 记 Y={x=41+22+.+nanm21,2,Lm∈R} V2={x=4b1+2b2+.+4,b,41,42,.4,∈R} 试证：V=V2·

V x a a a R = = 1 1 + 2 2 ++  m m 1 ,2 ,  , m  间 一般地， 由向量组a1 ,a2 ,,am所生成的向量空 为     . , , , , , , , , , 1 2 2 1 1 2 2 1 2 1 1 1 2 2 1 2 1 1 V V V x b b b R V x a a a R a a b b s s s m m m m s = = = + + +  = = + + +  试证： 记 设向量组 与向量组 等价，                 例 5  

证设x∈Y,则x可由a1,nm线性表示 因1，.，m可由b1,.,b,线性表示，故x可由b1,., b,线性表示，所以x∈V, 这就是说，若x∈V,则x∈V2, 因此VcV2· 类似地可证：若x∈V2,则∈V1, 因此V,cV 因为YcV,V,cV,所以Y=V2:

, , . 证 设xV1，则x可由a1  am线性表示 : , , 类似地可证 若x V2 则x V1 . 因为V1  V2，V2  V1，所以V1 = V2 线性表示， 因 可由 线性表示，故 可由 s m s b a , ,a b , ,b x b , , 1  1  1  . 所以x V2 这就是说，若x V1，则x V2， . 因此V1  V2 . 因此V2  V1