《线性代数》课程教学资源（PPT课件）第二章 矩阵及其运算 2.1 矩阵

矩阵及其适算 第一节矩阵 矩阵概念的引入 矩阵的定义 三 小结 思考题 返

·1850年西尔维斯特(Sylvester)首次 提出矩阵的概念 l858年卡莱(A.Cayley)建立了矩阵 的运算规则. ·应用：自然科学、工程技术、社会 科学等许多领域，如在观测、导航、 机器人的位移、化学分子结构的稳定 性分析、密码通讯、模糊识别，以及 计算机层析X射线照相术等方面，都 有广泛的应用. 上页 回

• 1850年西尔维斯特(Sylvester)首次 提出矩阵的概念. • 1858年卡莱(A. Cayley)建立了矩阵 的运算规则. • 应用：自然科学、工程技术、社会 科学等许多领域，如在观测、导航、 机器人的位移、化学分子结构的稳定 性分析、密码通讯、模糊识别，以及 计算机层析X射线照相术等方面，都 有广泛的应用

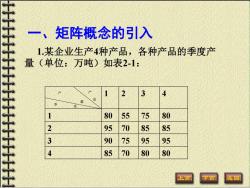
一、矩阵概念的引入 1.某企业生产4种产品，各种产品的季度产 量（单位：万吨)如表2-1： 3 度 80 55 75 80 2 95 70 85 85 3 90 75 95 95 4 85 70 80 80 页

一、矩阵概念的引入 1.某企业生产4种产品，各种产品的季度产 量（单位：万吨）如表2-1： 产 品 产 量 季 度 1 2 3 4 1 80 55 75 80 2 95 70 85 85 3 90 75 95 95 4 85 70 80 80

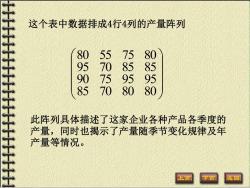
这个表中数据排成4行4列的产量阵列 0505 5050 5550 0550 此阵列具体描述了这家企业各种产品各季度的 产量，同时也揭示了产量随季节变化规律及年 产量等情况。 回

这个表中数据排成4行4列的产量阵列           85 70 80 80 90 75 95 95 95 70 85 85 80 55 75 80 此阵列具体描述了这家企业各种产品各季度的 产量，同时也揭示了产量随季节变化规律及年 产量等情况

1x1+L2X2+.+01mXn=b1 2.线性方程组 421x1+L22X2+.+02mXn=b2 ax+an2x2++amx=b 系数 的解取决于 a(6,j=1,2,n, 常数项b,(i=1,2,.,n) 上页

       + + + = + + + = + + + = n n nn n n n n n n a x a x a x b a x a x a x b a x a x a x b     1 1 2 2 21 1 22 2 2 2 11 1 12 2 1 1 2. 线性方程组 的解取决于 a (i, j 1,2, ,n), 系数 ij =  b (i , , ,n) 常数项 i = 1 2 

线性方程组的系数与常数项按原位置可排为 l12 b 1 2 @2n b, 对线性方程组的 研究可转化为对 这张表的研究 . b 上页 区回

              n n nn n n n a a a b a a a b a a a b         1 2 21 22 2 2 11 12 1 1 对线性方程组的 研究可转化为对 这张表的研究. 线性方程组的系数与常数项按原位置可排为

二、矩阵的定义 主二主二二二二主主二二二二主主 由m×n个数ag(i=1,2,m;j=1,2,n) 排成的n行n列的数表 11% L12 21 L22 am2 称为m×n矩阵.简称m×n矩阵.记作 上页

二、矩阵的定义 由 个数 排成的 行 列的数表 m n m n a (i m j n) ij = 1,2,  , ; = 1,2,  , m m mn n n a a a a a a a a a       1 2 21 22 2 11 12 1 称为 mn 矩阵.简称 m  n 矩阵. 记作

L12 A= L21 22 矩阵A的 m,n元 Am 简记为A=Ann=(a写)nn=(ag} 这m×n个数称为A的元素，简称为元 元素是实数的矩阵称为实矩阵 元素是复数的矩阵称为复矩阵 上页 区回

              = m m mn n n a a a a a a a a a A        1 1 21 22 2 11 12 1 简记为 ( ) ( ). ij m n A = Am n = aij = a   ( )元 矩阵 的 m n A , 这mn个数称为A的元素,简称为元. 元素是实数的矩阵称为实矩阵, 元素是复数的矩阵称为复矩阵

例如 03 主二主二二二二主主二二二二主主 5 -964 3 是一个2×4实矩阵， 13 6 2i） 2 是一个3×3复矩阵， 22 2. 2 是一个3×1矩阵， (2359) (4) 是一个1×4矩阵， 是一个1×1矩阵

例如       − 9 6 4 3 1 0 3 5 是一个 24 实矩阵,           2 2 2 2 2 2 13 6 2i 是一个 33 复矩阵,           4 2 1 是一个 31 矩阵, (2 3 5 9) 是一个 14 矩阵, (4) 是一个 11 矩阵

几种特殊矩阵 (1)行数与列数都等于n的矩阵A,称为n阶 方阵.也可记作An 13 6 2i 例如 2 2 2 是一个3阶方阵 、2 22 (2)只有一行的矩阵 A=(a1,2,0n) 称为行矩阵（或行向量） 区回

例如           2 2 2 2 2 2 13 6 2i 是一个3 阶方阵. 几种特殊矩阵 (2)只有一行的矩阵 ( , , , ), A = a1 a2  an 称为行矩阵(或行向量). (1)行数与列数都等于 n 的矩阵 A ，称为 n 阶 . 方阵.也可记作 An