《数学分析》课程教学课件（PPT讲稿）级数部分提纲

一、广义积分 1.无穷区间上的广义积分 ()定义 设f(x)∈C[a,+o),若im∫“f(x)d存在， 则称此极限为(x)在a,+∞)上的广义积分， 记作何fae)=mfae). 此时称广义积分收敛，否则发散

一、广义积分 1.无穷区间上的广义积分 (1)定义 此时称广义积分收敛，否则发散。 记 作 则称此极限为 在 上的广义积分 设 若 存 在 ( ) lim ( ) . ( ) [ , ) , ( ) [ , ), lim ( ) ,    + →+  + →+  = +   +  a x a B B a f x dx f x dx f x a f x C a f x dx

(2)判敛法则 ·比较判敛法 ·柯西判敛准则 2.无界函数的广义积分 (1)定义：设f(x)∈C[a,b-](8>0), imf)=o,若imf)存在，则称 此极限为f(x)在4，b]上的广义积分，记作 (d

(2)判敛法则 •比较判敛法 •柯西判敛准则 2.无界函数的广义积分    − → − → → + − + = =   −        b a b a b x b a f x dx f x dx f x a b f x f x dx f x C a b ( ) lim ( ) ( ) [ , ] , lim ( ) , lim ( ) , (1) : ( ) [ , ] ( 0), 0 0 此极限为 在 上的广义积分 记 作 若 存 在 则 称 定 义 设

(2)判敛法则 ·柯西判敛准则 3.两个重要的例 ka>≥0P>1收敛，ps1发散 2',p<1收效，p21发故. 要求 掌握广义积分的概念及判敛法则

(2)判敛法则 •柯西判敛准则 3.两个重要的例 ( 0), 1收敛， 1发散。 1 (1)     + dx a p p a x p , 1收敛， 1发散。 ( ) 1 (2)   −  dx p p x a b a p 要求 掌握广义积分的概念及判敛法则

二、数项级数 (一)数项级数的概念 设级数空，记5，一之“，称为级数的项 部分和。若数列S}存在极限S,则称级数 00 ∑4，收敛，且和为S,即∑4，=imSn=S. n=] =] 若{Sn}不收敛，称级数∑4n发散

二、数项级数 (一)数项级数的概念 若 不收敛 称级数 发散。 收 敛 且和为 即 部分和。若数列 存在极限 则称级数 设级数 记 称为级数的 项       = →  =  = =  = = = = 1 1 1 1 1 { } , , , lim . { } , , n n n n n n n n n n n k n k n n S u u S u S S S S u S u n

(二)级数的基本性质 1.若∑4n收敛，则imwn=0. n1->oo 2.设∑4，∑收敛，则 ●● ●● N= p (k4±k)=-k∑4±k之y n=1 n=1 n=] 3.级数去掉或加上有限项不改变级 数的敛散性

(二)级数的基本性质 1. lim 0. 1 = →  =  n n n 若 un 收敛，则 u       =  =  =  =  =  =  1 2 1 1 1 1 2 1 1 ( ) 2. , n n n n n n n n n n k u k v k u k v u v n 设 收敛，则 数的敛散性。 3.级数去掉或加上有限项，不改变级

0 4.若 ∑4n收敛，则任意加括号后 n=1 组成的新级数仍收敛，且其和不变。 (三)柯西收敛准则 0 ∑u收敛台He>0,3N>0,m>n>N, n=1 有Ln41+W+2十.4m<￡

组成的新级数仍收敛，且其和不变。 若  收敛，则任意加括号后  =1 4. n un (三)柯西收敛准则   + +          + +  =  n n m n n u u u u N m n N 1 2  1 0, 0, , 有 收 敛

(四)正项级数的判敛法则 1.比较判敛法 3达朗贝尔判敛法 4.柯西根式判敛法 5.柯西积分判敛法

3.达朗贝尔判敛法 4.柯西根式判敛法 5.柯西积分判敛法 (四)正项级数的判敛法则 1.比较判敛法

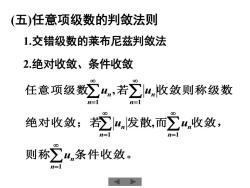
(五)任意项级数的判敛法则 1.交错级数的莱布尼兹判敛法 2.绝对收敛、条件收敛 任意项级数∑，若之l4收敛则称级数 绝对收敛；∑n发散，而∑，收敛， 则称∑4条件收敛

则 称 条件收敛。 绝对收敛；若 发 散 而 收敛，     =  =  = 1 1 1 , n n n n n n u u u 2.绝对收敛、条件收敛 任意项级数 若 收敛则称级数  =  =1 1 , n n n un u (五)任意项级数的判敛法则 1.交错级数的莱布尼兹判敛法

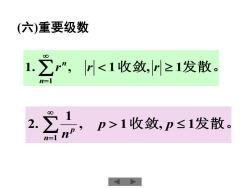
(六)重要级数 1.∑r”,r1收敛，p≤1发散。 n=1

(六)重要级数 1. , 1收 敛, 1发散。 1     = r r r n n , 1收 敛, 1发散。 1 2. 1     = p p n n p

要求 1.掌握级数的概念和性质 2.掌握正项级数的比较、 比值和根值判定准则 3.掌握任意项级数的绝对收敛和 条件收敛 4.交错级数的莱布尼茨判定准则

要求 1. 掌握级数的概念和性质 2. 掌握正项级数的比较、 比值和根值判定准则 3. 掌握任意项级数的绝对收敛和 条件收敛 4. 交错级数的莱布尼茨判定准则