《线性代数》课程授课教案（讲义）第四章 向量组及其线性组合

向量组及其线性组合 一、n维向量概念及表示方法 定义：n个有次序的数a,a,.,a,所组成的数组称为n维向量，这n个数称为该 向量的n个分量，第i个数a称为第i个分量。 实向量：分量全为实数的向量。 复向量：分量为复数的向量。 表示方法： n维向量写成一行，称为行向量，也就是行矩阵，通常用a,b,α'，B等表 示，如： a=(a,a,.,a） n维向量写成一列，称为列向量，也就是列矩阵，通常用a,b,a,B等表示， 如： a a) 向量的维数：向量中元素的个数叫做向量的维数。 注：1·行向量和列向量总被看作是两个不同的向量： 2.行向量和列向量都按照矩阵的运算法则进行运算： 3.当没有明确说明是行向量还是列向量时，都当作列向量 二、向量空间 将线性代数中的向量的概念与解析几何中介绍的向量的概念在n≤3下比 较：

向量组及其线性组合 一、n维向量概念及表示方法 定义： n 个有次序的数 1 2 , n a a a L 所组成的数组称为n 维向量，这 n 个数称为该 向量的n 个分量，第i 个数 i a 称为第i 个分量。 实向量：分量全为实数的向量。 复向量：分量为复数的向量。 表示方法： n 维向量写成一行，称为行向量，也就是行矩阵，通常用 , , , T T T T a b a b 等表 示，如： 1 2 ( , , , ) T n a = a a a L n 维向量写成一列，称为列向量，也就是列矩阵，通常用a b, , , a b 等表示， 如： 1 2 n a a a a æ ö ç ÷ ç ÷ = ç ÷ ç ÷ è ø M 向量的维数：向量中元素的个数叫做向量的维数。 注：１．行向量和列向量总被看作是两个不同的向量； ２．行向量和列向量都按照矩阵的运算法则进行运算； ３．当没有明确说明是行向量还是列向量时，都当作列向量. 二、向量空间 将线性代数中的向量的概念与解析几何中介绍的向量的概念在 n £ 3下比 较：

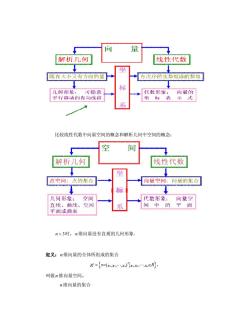
量 解析几何 线性代数 既有天小有方向的量 有次序的实数组成的数组 何形 代数形像： 量的 了多动的相长北安 坐装示式 系 比较线性代数中向量空间的概念和解析几何中空间的概念： 间 解析儿何 线性代数 坐 点窄御：点的集合 向宁间：向的集合 几何形象： 学间 代数形象 向最空 直线、线、空间 系 间中的 面 平面或曲面 n>3时，n维向量没有直观的儿何形象。 定义：n维向量的全体所组成的集合 R=x=xxR 叫做n维向量空间。 n维向量的集合

比较线性代数中向量空间的概念和解析几何中空间的概念： n > 3时， n 维向量没有直观的几何形象． 定义： n 维向量的全体所组成的集合 { ( 1 2 , , , ) 1 2 , , , } n n n T R = x R = Î x x x L x x x L ， 叫做n 维向量空间。 n 维向量的集合

π={x=(xx.x)lax,+a2x:++ax=b 叫做n维向量空间R中的n-1维超平面。 三、向量、向量组与矩阵 向量组：若干个同维数的列向量（或同维数的行向量）所组成的集合叫做向量组。 注：一个m×n的矩阵可以看作是n个m维列向量构成的向量组，同样也可以看 作是m个n维行向量构成的向量组。反之，n个m维列向量构成的向量组可以看 成是一个m×n的矩阵，m个n维行向量构成的向量组也可以看成是一个m×n的 矩阵，所以，向量的很多性质可以通过矩阵来考虑。 定义：给定向量组A:a1,a,.,an,对于任何一组实数k,k,.,kn,表达式 ka+ka2+.+k.an 称为向量组A:a,a2,.,a。,的一个线性组合，k,k,.,k。,称为这个线性组合的 系数。 定义：给定向量组A:a,a,a和向量b,如果存在一组数入，2.入使 b=a1+2a2+.+元am, 则向量b是向量组A:a,a2,.,a,的线性组合，这时称向量b能由向量组 A:a1,a2,0n,线性表示。 2 1 -5 10 0 例如：B= 0 3 ,61 10 0 84= 0 (0 1 定理：向量b能由向量组A:a%,a2,am,线性表示的充分必要条件是矩阵 A=(a,a2,a)的秩等于矩阵B=(a,a,.,an,b)的秩。 定义：设有两个向量组A:a,a2,.,an及B:B,B,B,若B组中的每个向量 都能由向量组A现象表示，则称向量组B能由向量组A线性表示，若向量组A与

{ ( 1 2 , , , )n 1 1 2 2 n n } T p = x b = x x x L a x +a x +L+ = a x 叫做n 维向量空间 n R 中的 n -1维超平面。 三、向量、向量组与矩阵 向量组：若干个同维数的列向量（或同维数的行向量）所组成的集合叫做向量组。 注：一个m n ´ 的矩阵可以看作是 n 个 m 维列向量构成的向量组，同样也可以看 作是m 个n 维行向量构成的向量组。反之，n 个 m 维列向量构成的向量组可以看 成是一个m n ´ 的矩阵，m 个n 维行向量构成的向量组也可以看成是一个 m n ´ 的 矩阵，所以，向量的很多性质可以通过矩阵来考虑。 定义：给定向量组 1 2 : , , , , A a a a L m ，对于任何一组实数 1 2 , , , , m k k k L 表达式 1 1 2 2 m m k a + k k a a + + L 称为向量组 1 2 : , , , , A a a a L m 的一个线性组合， 1 2 , , , , m k k k L 称为这个线性组合的 系数。 定义：给定向量组 1 2 : , , , , A a a a L m 和向量b ，如果存在一组数 1 2 , , , m l l l L ，使 1 1 2 2 m m b = l a + l a + + L l a ， 则向量 b 是向量组 1 2 : , , , , A a a a L m 的线性组合，这时称向量 b 能由向量组 1 2 : , , , , A a a a L m 线性表示。 例如： 1 2 3 4 2 1 0 0 0 5 0 1 0 0 , , , , 3 0 0 1 0 0 0 0 0 1 b e e e e æ ö æ ö æ ö æ ö æ ö ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ - ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ = = = = = ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø è ø è ø è ø 定理：向量 b 能由向量组 1 2 : , , , , A a a a L m 线性表示的充分必要条件是矩阵 1 2 ( , , , ) A = a a a L m 的秩等于矩阵 1 2 ( , , , , ) B b = a a a L m 的秩。 定义：设有两个向量组 1 2 : , , , A a a a L m及 1 2 : , , , B s b b b L ，若 B 组中的每个向量 都能由向量组 A 现象表示，则称向量组 B 能由向量组 A 线性表示，若向量组 A与

向量组B能相互线性表示，则称这两个向量组等价。 定理：向量组B:B,B,B能由向量组A:a,a,.,a线性表示的充分必要条 件是矩阵A=(a,a2,.,a)的秩等于矩阵(A,B)=(a1,a2,.,am,B,B2,.,B)的 秩，即R(A)=R(AB) 推论：向量组A:a,4,an与向量组B:月，B2,.,B等价的充分必要条件是 R(A)=R(B)=R(A,B),其中A和B是向量组A和B所构成的矩阵。 1 1Y 例1：设a,= 24-1 0 .b= 证明向量b能由向量组a,42,4,线 2 3 0 性表示，并求出表达式。 1 3 2) (3 例2：设a,= 1 ,42= 1 ，= b= 2 证明向量组a,a,与向 1 -1 3 1 2 量组，b,b等价。 定理：设向量组B:B,B,.,B,能由向量组A:a,a2,.,a线性表示，则 RB.B2,.,B,)≤Ra,a2,.,am) 总结：向量组B:,b,b,能由向量组4a,a,an线性表示， 一有矩阵K,使B=AK 一方程AX=B有解 R(A)=R (A,B) =R(A)≥R(B) 例3：设n维向量组A:a,2,.,an构成n×m矩阵A=(a,a,aw),n阶单位矩 阵E=(%,已2，.，en)的列向量叫做n维单位坐标向量组。证明：n维单位坐标向量 组e,e,能由向量组A线性表示的充分必要条件是R(A)=n

向量组 B 能相互线性表示，则称这两个向量组等价。 定理：向量组 1 2 : , , , B s b b b L 能由向量组 1 2 : , , , A a a a L m线性表示的充分必要条 件是矩阵 1 2 ( , , , ) A = a a a L m 的秩等于矩阵 1 2 1 2 ( , ) ( , , , , , , , ) A B = a a L L am s b b b 的 秩，即 R(A) = R(A B, ) 推论：向量组 1 2 : , , , A a a a L m 与向量组 1 2 : , , , B s b b b L 等价的充分必要条件是 R(A) = = R(B) R(A B, )，其中 A和 B 是向量组 A和 B 所构成的矩阵。 例 1：设 1 2 3 1 1 1 1 1 2 1 0 , , , 2 1 4 3 2 301 a a a b æ ö æ ö æ ö æ ö ç ÷ ç ÷ ç ÷ ç ÷ - ç ÷ ç ÷ ç ÷ ç ÷ = = = = ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø è ø è ø ，证明向量 b 能由向量组 1 2 3 a , , a a 线 性表示，并求出表达式。 例 2：设 1 2 1 3 1 1 , 1 1 1 3 a a æ ö æ ö ç ÷ ç ÷ - ç ÷ ç ÷ = = ç ÷ ç ÷ ç ÷ ç ÷ è- ø è ø ， 123 2 1 3 0 1 1 , , 1 0 2 1 2 0 b b b æ ö æ ö æ ö ç ÷ ç ÷ ç ÷ - ç ÷ ç ÷ ç ÷ = = = ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø è ø ，证明向量组 1 2 a a, 与向 量组 1 2 3 b , , b b 等价。 定理：设向量组 1 2 : , , , B b b b L s能由向量组 1 2 : , , , A a a a L m线性表示，则 1 2 ( , , , ) R b b b L s £ 1 2 ( , , , ) R a a a L m 总结： 1 2 1 2 , ,., , ,., B l m 向量组 ：b b b能由向量组A：a a a 线性表示 ， K B AX B R(A) R A B R A R B Û Û = Û = Þ ³ 有矩阵 ，使 =AK 方程 有解 （ ， ） （ ） （ ） 例 3：设n 维向量组 1 2 : , , , A m a a a L 构成n m´ 矩阵 1 2 ( , , , ) A m = a a a L ，n 阶单位矩 阵 1 2 ( , , , ) E n = e e e L 的列向量叫做n 维单位坐标向量组。证明：n 维单位坐标向量 组 1 2 , , , n e e e L 能由向量组 A线性表示的充分必要条件是 R( ) A n =

四、向量组的线性相关性 定义：给定向量组A:a,a2,.,心，如果存在不全为零的数k,k2,.,k,使 k4,+ka2+.+knan=0,则称向量组A:a1,a2,.,n是线性相关的。否则称它 线性无关。 注 (1)m=1时，即对于只有一个向量的向量组，若该向量为零，则是线性相关的， 若该向量不为零，则是线性无关的。 (2)m=2时，即对于含有两个向量的向量组，若它们线性相关，则这两个向 量对应分量成比例。 (3)m=3时，即含有三个向量的向量组，若它们线性相关，则这三个向量共面。 结论： (1)若n个向量构成的向量组线性相关，则在该向量组中至少有一个向量能由 其余的n-1个向量线性表示。 (2)如果向量组A中有某个向量能由其余的m-1个向量线性表示，则向量组 A是线性相关的。 定理：向量组a,a,.,a.线性相关的充分必要条件是它所构成的矩阵 A=(a,a,a)的秩小于向量个数m,向量组线性相关的充分必要条件是 R(A)=m 例4：试讨论n维单位坐标向量组的线性相关性 1 0 2 例5：已知a,= ,讨论向量组a,a,a,及向量组a,a的线性 5 相关性。 例6：已知向量组a,a,a,线性无关，b=a+a,b,=a,+a,b=a,+a,试证：向 量组b,b,b线性无关

四、向量组的线性相关性 定义：给定向量组 1 2 : , , , A a a a L m，如果存在不全为零的数 1 2 , m k， ，k k L ，使 1 1 2 2 0 m m k a + k k a a +L+ = ，则称向量组 1 2 : , , , A a a a L m是线性相关的。否则称它 线性无关。 注： （1）m = 1时，即对于只有一个向量的向量组，若该向量为零，则是线性相关的， 若该向量不为零，则是线性无关的。 （2） m = 2 时，即对于含有两个向量的向量组，若它们线性相关，则这两个向 量对应分量成比例。 （3）m = 3时，即含有三个向量的向量组，若它们线性相关，则这三个向量共面。 结论： （1） 若n 个向量构成的向量组线性相关，则在该向量组中至少有一个向量能由 其余的n -1个向量线性表示。 （2） 如果向量组 A中有某个向量能由其余的 m -1个向量线性表示，则向量组 A是线性相关的。 定理： 向 量组 1 2 , , , a a a L m 线 性相 关的 充分 必要条件 是它 所构 成的 矩阵 1 2 ( , , , ) A a a am = L 的秩小于向量个数 m ，向量组线性相关的充分必要条件是 R( ) A m= 例 4：试讨论n 维单位坐标向量组的线性相关性 例 5：已知 1 2 3 1 0 2 1 , 2 , 4 1 5 7 a a a æ ö æ ö æ ö ç ÷ ç ÷ ç ÷ = = = ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø è ø ，讨论向量组 1 2 3 a , , a a 及向量组 1 2 a a, 的线性 相关性。 例 6：已知向量组 1 2 3 a , , a a 线性无关， 1 1 2 2 2 3 3 3 1 b = a + a ,b = a + a , , b = + a a 试证：向 量组 1 2 3 b , , b b 线性无关

定理：若向量组A:a,a,a线性相关，则向量组B:C1,a2,Qn,&也线性 相关，反之，若向量组B:a,a2,.,an,a线性无关，则向量组A:a1,a2,.,an也 线性无关。 定理：m个n维向量组成的向量组，当维数n小于向量个数m时一定线性相关， 特别地，n+1各n维向量一定线性相关。 定理：设向量组A:a1,a线性无关，而向量组B:a1,a,a.,b线性相关， 则向量b必能由向量组A:a,a,a线性表示，且表示式是唯一的。 例7：设向量组a1,42,4,线性相关，向量组a2,a,a,线性无关，证明 (1)a能由a2,a,线性表示：(2)a,不能由a1,a2,a线性表示。 §3向量组的秩 前面我们已经学习了矩阵的秩，然后我们有讨论了矩阵与向量组的对应关 系，这节课我们来学习向量组的秩。首先给出向量组的秩的定义。 1、定义：设有向量组A,如果在A中能选出r个向量a,a,.,a,满足 (1)向量组a1,a,a,线性相关： (2)向量组A中任意r+1个向量（如果A中有r+1个向量的话）都线性相关。 那么称向量组A,是向量组A的一个最大无关向量组（简称最大无关组）：最大无 关组中所含向量个数r称为向量组A的秩，记作R,或R(a,a,a) 注意：(1)只含零向量的向量组没有最大无关组，规定它的秩为零。 (2)线性无关向量组的极大无关组为其本身 (3)向量组的最大无关组不一定唯一。 (与矩阵的最高阶非零子式不一定唯一类似) 既然矩阵与向量组有一一对应的关系，那么我们给出的问题是矩阵的秩和向 量组的秩之间存在着什么样的关系？看下面的定理。 定理：矩阵的秩等于它的列向量组的秩，也等于它的行向量组的秩

定理：若向量组 1 2 : , , , A a a a L m线性相关，则向量组 1 2 1 : , , , , B a a L a a m m+ 也线性 相关，反之，若向量组 1 2 1 : , , , , B a a L a a m m+ 线性无关，则向量组 1 2 : , , , A a a a L m也 线性无关。 定理： m 个n 维向量组成的向量组，当维数n 小于向量个数m 时一定线性相关， 特别地，n +1各n 维向量一定线性相关。 定理：设向量组 1 2 : , , , A a a a L m线性无关，而向量组 1 2 : , , , , B b a a a L m 线性相关， 则向量b 必能由向量组 1 2 : , , , A a a a L m线性表示，且表示式是唯一的。 例 7：设向量组 1 2 3 a , , a a 线性相关，向量组 2 3 4 a , , a a 线性无关，证明： （1）a1能由 2 3 a a, 线性表示； （2）a4 不能由 1 2 3 a , , a a 线性表示。 §3 向量组的秩 前面我们已经学习了矩阵的秩，然后我们有讨论了矩阵与向量组的对应关 系，这节课我们来学习向量组的秩。首先给出向量组的秩的定义。 1、定义：设有向量组 A,如果在 A中能选出 r 个向量 1 2 , , , a a a L r ，满足 （1）向量组 0 1 2 : , , , A a a a L r 线性相关； （2）向量组 A中任意 r +1个向量（如果 A中有 r +1个向量的话）都线性相关。 那么称向量组 A0 是向量组 A的一个最大无关向量组（简称最大无关组）；最大无 关组中所含向量个数r 称为向量组 A的秩，记作 RA ，或 1 2 ( , ,) R n a a a L 注意：（1）只含零向量的向量组没有最大无关组，规定它的秩为零。 （2）线性无关向量组的极大无关组为其本身。 （3）向量组的最大无关组不一定唯一。 （与矩阵的最高阶非零子式不一定唯一类似） 既然矩阵与向量组有一一对应的关系，那么我们给出的问题是矩阵的秩和向 量组的秩之间存在着什么样的关系？看下面的定理。 定理：矩阵的秩等于它的列向量组的秩，也等于它的行向量组的秩

注意：该定理给出矩阵的秩与向量组的秩之间存在的关系，所以，我们可以看出 要想求向量组的秩就可以求由向量组构成的矩阵的秩。 例1：求向量组a=1,a,=2,a=4的一个极大无关组. (5 (7 解：Ra,a)=R(a2,a)=R(a,a)=R(a1,a2,a,) 由此可知a1,a2和a2,a以及a1,a,都是所求向量组的最大无关组 结论：向量组的最大无关组不是唯一的。但注意，虽然向量组的最大无关组不是 唯一的，但每一个最大无关组中所含向量的个数是惟一的. 推论：（最大无关组的等价定义）设向量组A:α1，a2,a,是向量组A的一个部 分组，且满足： (1)向量组4线性无关。 (2)向量组A的任一向量都能由向量组A,线性表示，那么向量组A,便是向量组 A的一个最大无关组。 定理：向量组6，b,.b能由向量组a,4,an线性表示的充分必要条件是 R(a,a,.,an)=R(a,a,.,a,b,.b) 结论：这里R(a,a,a)即可理解为向量组的秩，也可以理解为矩阵的秩。 定理：若向量组B能由向量组A线性表示，则R≤R, 结论：设向量组B能由向量组A线性表示，且它们的秩相等，证明向量组A与向 量组B等价。 前面我们讨论了如何求矩阵的最高阶非零子式，那么我们考虑矩阵的最高阶非零 子式和向量组的最大无关组之间存在着什么样的关系呢？我们给出，矩阵的最高 阶非零子式所在的列构成矩阵列向量组的最大无关组，由此，我们可以得出如何 求向量组的最大无关组

注意：该定理给出矩阵的秩与向量组的秩之间存在的关系，所以，我们可以看出 要想求向量组的秩就可以求由向量组构成的矩阵的秩。 例 1：求向量组 1 2 3 1 0 2 1 , 2 , 4 1 5 7 æ ö æ ö æ ö ç ÷ ç ÷ ç ÷ = = = ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø è ø a a a 的一个极大无关组． 解： 1 2 2 3 1 3 1 2 3 R(a ,a ) = R(a ,a ) = = R R (a ,a ) (a ,a a, ) 由此可知 1 2 a a, 和 2 3 a a, 以及 1 3 a a, 都是所求向量组的最大无关组 结论：向量组的最大无关组不是唯一的。但注意，虽然向量组的最大无关组不是 唯一的，但每一个最大无关组中所含向量的个数是惟一的． 推论：（最大无关组的等价定义）设向量组 0 1 2 : , , , A a a a L r 是向量组 A的一个部 分组，且满足： （1） 向量组 A0 线性无关。 （2）向量组 A的任一向量都能由向量组 A0 线性表示，那么向量组 A0 便是向量组 A的一个最大无关组。 定理：向量组 1 2 , , l b b b L 能由向量组 1 2 , m a a a L 线性表示的充分必要条件是 1 2 ( , , , ) R m a a a L 1 2 1 2 ( , , , , , , ) R m l = a a L L a b b b 结论：这里 1 2 ( , , , ) R m a a a L 即可理解为向量组的秩，也可以理解为矩阵的秩。 定理：若向量组 B 能由向量组 A线性表示，则 R R B A £ 。 结论：设向量组 B 能由向量组 A线性表示，且它们的秩相等，证明向量组 A与向 量组 B 等价。 前面我们讨论了如何求矩阵的最高阶非零子式，那么我们考虑矩阵的最高阶非零 子式和向量组的最大无关组之间存在着什么样的关系呢？我们给出，矩阵的最高 阶非零子式所在的列构成矩阵列向量组的最大无关组，由此，我们可以得出如何 求向量组的最大无关组

12-10) %4 求矩阵A的列向量组的一个最大无关组，并 10-36-1 2220 把不属于最大无关组的列向量用最大无关组线性表示。 [2-1-112 例：设矩阵A= 11-214 4-62-24 ,求矩阵A的列向量组的一个最大无关组， 36-979 并把不属于最大无关组的列向量用最大无关组线性表示。 解：对A施行初等行变换化为行阶梯形矩阵 [11-214 401-10 知(A)=3,故列向量组的最大无关组含3个向量。 0001-3 00000 而三个非零行的非零首元在1,2,4列，故4,4，a,为列向量组的最大无关组。 为把a,a,用a,a,a,线性表示，继续化行最简行矩阵 「10-1041 r01-103 A 0001-3 因此，表示式为：a=-a-aa5=4a+3a,-3a 00000」 结论：本例的解法表明：如果矩阵A与B的行向量组等价，则方程组红=0与 Bx=0同解，从而A的列向量组各向量之间与B的列向量组各向量之间有相同的 线性关系。如果B是一个行最简形矩阵，则容易看出B的列向量组各向量之间的 线性关系，从而也就得到A的列向量组各向量之间的线性关系

例：设矩阵 1 2 1 0 4 5 2 2 1 1 5 2 0 3 6 1 2 2 2 0 A æ ö - ç ÷ ç ÷ = - ç ÷ ç ÷ - - ç ÷ è ø ，求矩阵 A 的列向量组的一个最大无关组，并 把不属于最大无关组的列向量用最大无关组线性表示。 例：设矩阵 2 1 1 1 2 1 1 2 1 4 4 6 2 2 4 3 6 9 7 9 A é ù - - ê ú - = - - ë û - ，求矩阵 A的列向量组的一个最大无关组， 并把不属于最大无关组的列向量用最大无关组线性表示。 解：对 A施行初等行变换化为行阶梯形矩阵 1 1 2 1 4 0 1 1 1 0 0 0 0 1 3 0 0 0 0 0 r A é ù - ê ú - - ë û 知 R A( ) 3 = ，故列向量组的最大无关组含 3 个向量。 而三个非零行的非零首元在 1，2，4 列，故 1 2 4 a , , a a 为列向量组的最大无关组。 为把 3 5 a a, 用 1 2 4 a , , a a 线性表示，继续化行最简行矩阵： 1 0 1 0 4 0 1 1 0 3 0 0 0 1 3 0 0 0 0 0 r A é ù - ê ú - - ë û 因此，表示式为： 3 1 2 5 1 2 4 a = -a - a ;a = 4a + - 3 3 a a 结论：本例的解法表明：如果矩阵 A 与 B 的行向量组等价，则方程组 Ax = 0与 Bx = 0 同解，从而 A的列向量组各向量之间与 B 的列向量组各向量之间有相同的 线性关系。如果 B 是一个行最简形矩阵，则容易看出 B 的列向量组各向量之间的 线性关系，从而也就得到 A的列向量组各向量之间的线性关系